Министерство образования Российской Федерации

Российский государственный профессионально-педагогический университет

Кафедра высшей математики

Аналитическая геометрия и элементы линейной алгебры

Индивидуальные домашние задания

Варианты 21 - 27

Екатеринбург 2002

Аналитическая геометрия и элементы линейной алгебры: Индивидуальные домашние задания / Екатеринбург, 2002. Варианты 21 - 27. 56 с.

Составители: доц., канд. физ.-мат. наук Просвиров Александр Сергеевич, ст. препод. Горюн Тамара Васильевна.

© Российский государственный

профессионально-педагогический

университет, 2002 г.

Вариант № 21

1. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ: ПРОСТЕЙШИЕ ЗАДАЧИ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ НА ПЛОСКОСТИ; ПРЯМАЯ НА ПЛОСКОСТИ; ЛИНИИ ВТОРОГО ПОРЯДКА НА ПЛОСКОСТИ

1. Найти уравнение прямой, которая проходит через начало координат и:

а) параллельна прямой ; б) перпендикулярна прямой;

в) образует угол в с прямой.

2. В равнобедренном прямоугольном треугольнике даны координаты вершины острого угла (0,2) и уравнение противолежащего катета: . Составить уравнения двух других сторон треугольника.

3. Даны середины сторон треугольника ,,. Составить уравнения его сторон.

4. Даны вершины треугольника А(-4, –5),В(-2, -1),С(0, 1). Написать уравнение перпендикуляра, опущенного из вершины А на медиану треугольника АВС, проведенную из вершины В.

5. Отрезок, ограниченный точками А(-6, 2) и В(0, 8), разделен на три равные части. Определить координаты точек деления.

6. Даны уравнения двух сторон треугольника и. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точкеР(6,3).

7. Даны две смежные вершины квадрата А(3, 2) и В(0, 6). Составить уравнения его сторон.

8. Точка Е(6, 4) является центром квадрата, одна из сторон которого лежит на прямой: . Составить уравнения прямых, на которых лежат остальные стороны квадрата.

9. Установить, какие линии определяются в полярных координатах следующими уравнениями (построить их на чертеже):

а); б); в); г);

д) ; е).

10. Установить, какая линия определяется уравнением . Найти координаты ее центра, полуоси, эксцентриситет. Сделать чертеж.

11. Составить уравнение эллипса и найти координаты его центра, полуоси, эксцентриситет, если известно, что левый фокус эллипса находится в правой вершине гиперболы: , при этом один из концов большей оси эллипса находится в точке(17, 0), а другой – в вершине параболы .

12. Составить уравнение линии, для каждой точки которой расстояние от точки А(5, 6) вдвое меньше расстояния от прямой . Определить, какая это линия; сделать чертеж.

13. Линия задана уравнением в полярной системе координат. Требуется:

а) построить линию по точкам, начиная от дои придаваязначения через промежуток;

б) найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью;

в) по полученному уравнению определить, какая это линия.

2. Определители. Базис в пространстве. Координаты вектора

14. Вычислить определители:

а) по правилу треугольника;

б) разложением по элементам первой строки;

в) разложением по элементам второго столбца;

г) сведением к треугольному виду:

а) , б), в), г).

15. Даны векторы: ₁=(1,2,3); ₂=(2,-3,4); ₃=(–1,-2,2);

=(13,-9,14) в некотором базисе. Показать, что первые три вектора сами образуют базис и найти координаты вектора в этом базисе.

3. Линейные операции над векторами. Проекция вектора на ось. Скалярное, векторное и смешанное произведения векторов

16. Найти координаты единичного вектора (орта) , сонаправленного с вектором =(2,1,–6).

17. Два вектора =(–0,-4,3)и =(–2,6,-3) приложены к одной точке. Найти координаты:

а) ортов ивекторови;

б) вектора +;

в) вектора , направленного по биссектрисе угла между векторамиипри условии, что.

18. Даны точки А(3, 6, 1), В(6, 5, 9), С(4, 2, 5), D(6, 4, 6). Вычислить .

19. Найти проекцию вектора =(3, -5, 2) на ось, составляющую с координатными осями ,углы,, а с осью- острый угол.

20. Дан квадрат ABCD (обозначение вершин принято по ходу часовой стрелки), длина стороны которого равна 2. Точка О выбрана в плоскости квадрата так, что ,. Найти.

Указание. Использовать последовательность действий:

а) ввести декартову прямоугольную систему координат с началом в точкеО так, чтобы ось была направлена по вектору, а осьнаправить в сторону расположения квадрата;

б) подсчитав длину диагонали квадрата, убедиться (по теореме Пифагора), что– прямоугольный (), а поэтому;

в) найти координаты вектора , найти координаты вектора(очевидно) и вектора, используя равенство, найти координаты вектора;

г) зная координаты векторов и, найти, где,.

21. Векторы исовпадают со сторонами треугольника. Вычислить длину медианыАМ, проведенной из вершины А, если ,,.

22. Найти величину острого угла между диагоналями параллелограмма, построенного на векторах и.

23. Вычислить координаты векторного произведения и его длину, если =(–1, 3, 1), .

24. Даны вершины треугольника А(4, 6, 7),В(2, 5, 1) и С(4, 7, 2). Найти площадь треугольника и длину высоты, опущенной из вершины А.

25. Найти координаты вектора , перпендикулярного векторам и ,если и векторсоставляет с осьютупой угол.

26. Вычислить , если,,.

27. Вычислить смешанное произведение векторов ,,.

28. Лежат ли четыре точки А(-3, 1, 1), В(-3, 0, 1), С(-2, 1, 0), D(–1, 1, -1) в одной плоскости?

29. Вычислить объем пирамиды, вершины которой А(3, -4, 3), В(5, -1, 7), С(9, -2, 5), D(6, 3, 4).

30. Вектор перпендикулярен к векторами. Вычислить, если ,,,,а тройка векторов – правая.

4. Аналитическая геометрия в пространстве: плоскость и прямая в пространстве; поверхности второго порядка

31. Составить уравнение плоскости, проходящей через точку , параллельную плоскости.

32. Составить уравнение плоскости, проходящей через точку и прямую.

33. Составить уравнение плоскости, проходящей через прямую перпендикулярно плоскости.

34. Составить уравнение плоскости, которая проходит через точку перпендикулярно двум плоскостям:,.

35. Найти расстояние от точкидо плоскости.

36. Составить уравнение плоскости, проходящей через точку перпендикулярно к прямой.

37. Составить параметрические уравнения прямой .

38. Составить канонические уравнения прямой, проходящей через точку , параллельно прямой,,.

39. Найти координаты точки пересечения прямой и плоскости.

40. Найти тупой угол между прямыми:

, ,;

, ,.

41. Найти координаты точки Q, симметричной точке Р(-2, 5, 3) относительно плоскости .

42. Найти координаты точки Q, симметричной точке Р(4, 5, 4) относительно прямой .

43. Вычислить расстояние от точкидо прямой.

44. Из всех прямых, пересекающих две прямые и. Найти канонические уравнения той прямой, которая была бы параллельна прямой.

Указание. Произвести последовательность действий:

а) найти координаты нормального вектора к плоскости, проходящей через прямую, параллельно прямой, где (2, 3, 1) – направляющий вектор прямой , (8, 7, 1) – направляющий вектор прямой ;

б) составить общее уравнение плоскости , как плоскости, проходящей через точкус нормальным вектором;

в) аналогично найти координаты нормального вектора к плоскости, проходящей через прямую, параллельно прямой, где (5, 4, 1), (8, 7, 1) – направляющие векторы прямых исоответственно;

составить общее уравнение плоскости , как плоскости, проходящей через точкус нормальным вектором;

г) искомая прямая есть линия пересечения плоскостейи, зная их общие уравнения, найти канонические уравнения искомой прямой.

45. Даны координаты вершины пирамиды А₁(2, 4, 3), А₂(6, 3, 1), А₃(3, 3, 4), А₄(3, 0, 5). Найти:

1. угол между ребрами А₁А₂ и А₁А₄;

2. угол между ребром А₁А₄ и гранью А₁А₂А₃;

3. уравнение прямой А₁А₂;

4. уравнение плоскости А₁А₂А₃;

5) уравнение высоты, опущенной из вершины А₄ на грань А₁А₂А₃.

46. Построить эскиз тела, ограниченного поверхностями:

а) ,,;

б),.

5. Элементы линейной алгебры: системы линейных уравнений; матрицы; линейное векторное пространство; линейные операторы

47. Решить систему линейных уравнений методом Гаусса

48. Найти все вещественные матрицы, перестановочные с матрицей .

49. Найти матрицу , где

А=, В=, С=.

50. Найти ранг матриц:

а) ; б).

51. Дана система линейных уравнений

Доказать ее совместность и решить тремя способами:

а) методом Гаусса;

б) средствами матричного исчисления;

в) по формулам Крамера.

52. Является ли линейным пространством:

а) множество всех многочленов (от одного переменного) с действительными коэффициентами степени ;

б) множество всех таких многочленов степени 7.

53. Найти все значения , при которых векторлинейно выражается через векторы, если =(1, -2,),=(1, 2, 3),=(1, 3, 5),=(2, 1, 0).

54. Выяснить, является ли данная система векторов из линейно зависимой? =(1, 0, 0, 1),=(0, 1, 1, –1),=(1, -2, 1, -1),=(-1, 1, -1, 1).

55. Выяснить геометрический смысл действия линейных операторов, данных в пространстве , матрицы которых относительно ортонормированного базисаимеют вид:

а) ; б).

56. В пространстве всех вещественных матриц второго порядка дан оператор: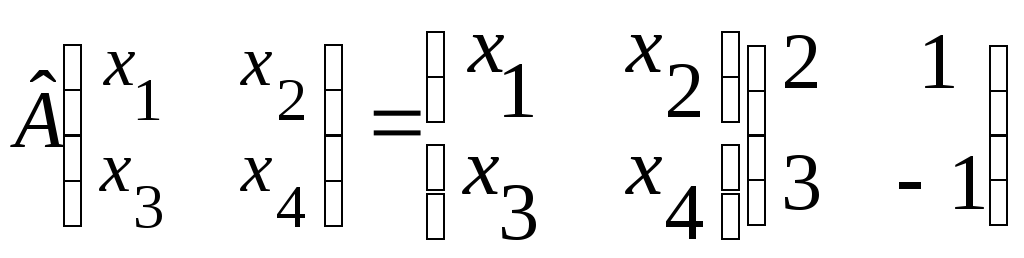. Доказать линейность оператораи найти его матрицу в базисе,,,.

57. В евклидовом пространстве линейный операторпроецирует векторы на плоскость, а линейный операторпереводит векторысоответственно в векторы

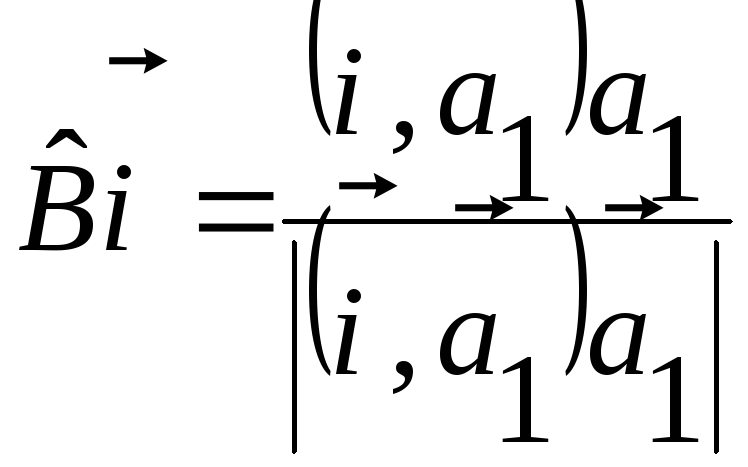, ,, где,. Найти матрицы линейных операторов,,в базисе.

58. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей .