36. Основной закон релятивистской динамики материальной точки.

На опытах с быстро движущимися электронами было установлено, что масса тела зависит от скорости движения, а именно возрастает с увеличением скорости по закону,гдеm₀ – масса покоя, m-релятивистская масса.

Из принципа относительности Эйнштейна, утверждающего инвариантность всех законов природы при переходе от одной инерциальной системы отсчёта к другой, следует условие инвариантности уравнений физических законов относительно преобразований Лоренца.

Основной закон динамики Н:

оказывается также инвариантным по отношению к преобразованиям Лоренца, если в нём справа стоит производная по времени от релятивистского импульса.

Основной закон релятивистской динамики мт имеет вид:

- релятивистский импульс мт.

В силу однородности пространства закон сохранения релятивистского импульса: релятивистский импульс замкнутой системы сохраняется, т.е. не изменяется с течением времени.

37. Закон взаимосвязи массы и энергии.

Найдём кинетическую энергию релятивистской частицы (материальной точки).

или.

Учитывая, что , и подставив в. выражениеполучим :

.

Преобразовав данное выражение с учётом того, что и формулыпридём к выражению:

,

т.е. приращение кинетической энергии частицы пропорционально приращению её массы. Проинтегрировав получим:

, или кин. энергия релятивистской частицы имеет вид:

.

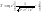Это выражение при скоростях переходит в классическое:

.Любое изменение массы сопровождается изменением полной энергии материальной точки,.

Отсюда перейдём к зависимости между полной энергией тела E и его массой m :

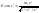.Это уравнение , также как и предыдущее выражает фундаментальный закон природы – закон взаимосвязи (пропорциональности) массы и энергии: полная энергия системы равна произведению её массы на квадрат скорости света в вакууме.

Этот закон, учитывая , можно записать в виде:

, откуда следует, что покоящееся тело (Т=0) также обладает энергией:, называемойэнегией покоя.

В силу однородности времени выполняется закон сохранения энергии: полная энеогия замкнутой системы сохраняется, т.е. не изменяется стечением времени.

Из формул . инайдём релятивистское соотношение между полной и энергией частицы:

,

.

Энергия связи системы равна работе, которую необходимо затратить, чтобы разложить эту систему на составные части (например атомное ядро на протоны и нейтроны). Энергия связи системы:

,где - масса покояi-й частицы в свободном состоянии; - масса покоя системы, состоящей изn частиц.

38. Модель идеального газа. Изозаконы.

В МКТ пользуются моделью идеального газа, согласно которой:

1) собственный объём молекул газа пренебрежимо мал по сравнению с объёмом сосуда.

2) между молекулами газа отсутствуют силы взаимодействия.

3) столкновения молекул газа между собой и стенками сосуда абсолютно упругие.

Модель идеального газа можно использовать при изучении реальных газов, т.к. они в условиях, близких к нормальным (кислород, гелий), а также при низких давлениях и высоких температурах близки по своим свойствам к идеальному газу(иг).

Опытным путём, ещё до появления МКТ, был установлен целый ряд законов, описывающих поведение иг’ов:

1. Закон Бойля-Мариотта (изотерма): для данной массы газа при постоянной температуре произведение давления газа на его объём есть величина постоянная:

изотерма – кривая (гипербола), изображающая зависимость между величинами P и V , характеризующими св-ва вещ-ва, при постоянной Т.

2. Закон Гей-Люссака(изобара):

1. объём данной массы газа при постоянном давлении изменяется линейно с температурой:

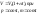
2. (Шарля) давление данной массы газа при постоянном объёме изменяется линейно с температурой.

В этих уравнениях t – температура по шкале Цельсия, р₀ и V₀ – давление о объём при 0^оС, коэффициент .

Изобарный – процесс, протекающий при постоянном давлении.

изохорный – процесс, протекающий при постоянном объёме.

Вводя в формулы итермодинамическую температуру, получим: