РГЗ-4

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ВОЛОГОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА ЭЛЕКТРОТЕНИКИ

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЭЛЕКТРОТЕХНИКИ

ЧАСТЬ 2

ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ДЛИННЫХ ЛИНИЯХ

Методические указания по выполнению

расчетно-графических работ

Факультет: электроэнергетический

Специальность: 100400 – электроснабжение

Вологда, 2005

УДК: 371.315.10

Теоретические основы электротехники. Часть 2. Переходные процессы в длинных линиях. Методические указания по выполнению расчетно-графических работ. – Вологда: ВоГТУ, 2005. - с.

Методические указания содержат краткие теоретические сведения, пример расчета и оформления расчетно-графической работы, варианты заданий расчетных работ.

Составители: Г.Л.Ганичев, канд. техн. наук, доц.

В.В.Реутов, канд. техн. наук, доц.

Рецензент:

ВВЕДЕНИЕ

Настоящие методические указания предназначены для студентов всех форм обучения по специальности 100400, изучающих курс «Теоретические основы электротехники» и содержит методические указания по анализу переходных процессов в длинных линиях, а также варианты заданий для расчета по данной теме.

Расчетно-графические работы служат для закрепления теоретической части курса, с которой студенты знакомятся на лекциях и практических занятиях.

Задания соответствуют стандарту специальности и рассчитаны на индивидуальное выполнение студентами во внеаудиторное время.

1. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

В цепях с распределенными параметрами, например, в однородных линиях, большой интерес представляют собой непериодические процессы, т.е. переходные процессы при включении и выключении линии, при воздействии на линии грозовых разрядов и т.п.

Во всех случаях при анализе переходных процессов в линиях с распределенными параметрами необходимо решить систему дифференциальных уравнений в частных производных при заданных граничных и начальных условиях.

Для однородной двухпроводной линии с распределенными параметрами система дифференциальных уравнений имеет вид:

, .

Для неискажающей линии решение этих уравнений может быть представлено виде суммы двух функций

,

.

где

- коэффициент затухания,

- волновое сопротивление линии,

- скорость распространения.

В линии без потерь, когда можно принять , , , решение для напряжения в линии имеет вид:

.

1. Волны в линии

Функция определяет прямую волну напряжения, распространяющуюся вдоль линии со скоростью v в направлении возрастания координаты x .

Действительно, пусть в фиксированный момент времени напряжение волны распределено вдоль линии по координате x так, как это показано на рис.1. Обозначим в точке с напряжение .

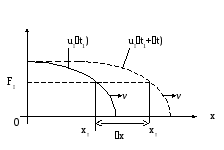
Рис.1.

Найдем значение в точке , лежащей справа от на расстоянии в момент времени .

При нашем предположении, что распространяется со скоростью v слева направо, имеем .

Тогда получим:

,

т.е. принимает в точке такое же значение, как и в точке с запаздыванием во времени на , необходимое для прохождения волной расстояния .

Таким образом, если известно значение в начале линии, то значение в любой точке, отстоящей от начала линии в направлении распространения волны на расстоянии x может быть найдено добавлением к аргументу .

Аналогично, функция определяет обратную волну напряжения, распространяющуюся со скоростью v в направлении убывания x , т.е. от начала к концу.

Таким образом, в линии без потерь напряжение и ток могут быть представлены в виде суммы двух волн

,

,

, .

При анализе переходных процессов в однородной линии примем следующие допущения:

- длина линии мала по сравнению с длиной волны. В этом случае предполагается, что внешние э.д.с постоянны. Такое предположение допустимо, так как рассматриваемые явления протекают настолько быстро, что в случае синусоидальной э.д.с ее величина за время пробега волны вдоль всей линии может измениться лишь весьма незначительно;

- рассматриваем процессы в линии без потерь. В этом случае фронт волны при ее движении вдоль линии не изменяется;

- процессы переключения осуществляются мгновенно.

2. Расчет прямых волн в линии

Расчет прямых волн в линии проводится до момента времени, когда обратная волна, отразившись от нагрузки в конце линии, не вернется к началу линии в месте подключения источника.

В этом случае в каждой точке линии, где существует только прямая (падающая) волна, справедливо соотношение

,

т.е. прямая (падающая) волна в линии может быть найдена как падение напряжения на волновом сопротивлении линии.

3. Расчет отраженных волн напряжения и тока

Рассмотрим случай, когда прямые волны напряжения и тока достигли конца однородной линии с волновым сопротивлением z и замкнутой на сколь угодно сложную цепь с сосредоточенными параметрами.

В этом случае для точек в конце линии имеем:

и .

Решив совместно, получим

.

Из этой зависимости следует, что ток в конце линии можно найти как ток, возникающий в эквивалентной (расчетной) схеме (рис.2), включаемой под напряжение и состоящей из активного сопротивления, равного волновому сопротивлению линии, и последовательно соединенной с ним оконечной цепи.

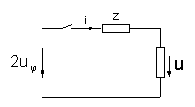
Рис.2.

Следует отметить, что схема справедлива для определения токов и напряжений только в точках, расположенных в конце линии.

Отсчет времени в выражениях для тока и напряжения, т.е. замыкание ключа в расчетной схеме, начинается от момента прихода прямой волны напряжения от источника к концу линии.

Определив ток i в конце линии, рассчитав переходный процесс в расчетной схеме, находим отраженные волны напряжения и тока для точек в конце линии из соотношений

, .

Для произвольных точек линии напряжение и ток можно определить, если учесть запаздывание прихода волны в каждую последующую точку линии, при распространении ее от конца линии к ее началу, заменой аргумента t в и

для точек в конце линии на аргумент , где y - расстояние, отсчитываемое от конца линии к ее началу.

Подставив , получим аргумент .

Выражения и позволяют рассчитать значения напряжения и тока отраженной волны в произвольный момент времени и в любой точке линии.

Отмечаем, что полученные выражения справедливы до момента прихода отраженных волн к месту подключения источника вначале линии.

2. Пример расчета волн напряжения и тока

Рассмотрим применение вышеприведенной методики для расчета переходного процесса в однородной линии при подключении ее к источнику постоянного напряжения.

Схема цепи приведена на рис.3. Там же приведены значения всех параметров элементов цепи и другие условия.

Требуется рассчитать и построить графики распределения напряжений и токов вдоль линий для момента времени, когда отраженная волна во второй линии пройдет до точки, расположенной в середине линии.

В Приложении 1 приведен пример расчета распределения напряжения и тока вдоль линий.

3. Варианты заданий на расчет

Варианты заданий на расчет приведены в Приложении 2.

Вариант индивидуального задания на расчет определяется четырехзначным шифром.

Шифр варианта задания состоит из четырех цифр:

- первая цифра – номер схемы элементов неоднородности из рис.9;

- вторая цифра – номер строки из таблицы №2 с параметрами схемы на

рис.9;

- третья цифра – номер схемы нагрузки из рис.10;

- четвертая цифра – номер строки из таблицы №2 с параметрами схемы

нагрузки на рис.10.

ЛИТЕРАТУРА

1. Теоретические основы электротехники: В 3-х т. Учебник для вузов. Том 1.-4-е изд./ К.С. Демирчян, Л.Р. Нейман, Н.В. Коровкин, В.Л. Чечурин.- СПб.: Питер, 2003.- 463 с.: ил.

2. Дьяконов, В. MATHCAD 8/2000./ В. Дьяконов. Специальный справочник - СПб: Питер, 2000.- 592 с.: ил.

СОДЕРЖАНИЕ стр.

Введение…………………………………………………………………

1. Основные теоретические положения……………………………….

2. Пример расчета волн напряжения и тока………………………….

3. Варианты заданий на расчет………………………………………..

Литература………………………………………………………………

Приложения……………………………………………………………..

9