Лекция 19.

п.17. Транспортная задача.

17.1. Постановка транспортной задачи

по критерию стоимости в матричной форме.

Рассмотрим простейший вариант модели транспортной задачи (ТЗ), когда речь идет о рациональной перевозке некоторого однородного продукта от производителя к потребителям; при этом имеется баланс между суммарным спросом потребителей и возможностями поставщиков по их удовлетворению. Причем потребителям безразлично, из каких пунктов производства будет поступать продукция, лишь бы их заявки были полностью удовлетворены. Так как от схемы прикрепления потребителей к поставщикам существенно зависит объем транспортной работы, возникает задача о наиболее рацио-нальном прикреплении, правильном направлении перевозок грузов, при котором потреб-ности полностью удовлетворяются, вся продукция от поставщиков вывозиться, а затраты на транспортировку минимальны.

Транспортную задачу можно сформулировать следующим образом, представив ее в виде таблицы, которую называют распределительной. Распределительную таблицу назы-вают иногда табличной или матричной моделью ТЗ.

Поставщики	Потребители				Запас груза, ai
	B1	B2	…	Bn
A1	c11 x11	c12 x12	…	c1n x1n	a1
A2	c12 x12	c22 x22	…	c2n x2n	a2
…	…	…	…	…	…
Am	cm1 xm1	cm2 xm2	…	cmn xmn	am
Потребность в грузе, bj	b1	b2	…	bn

В m пунктах отправления A₁, …, A_m сосредоточен однородный груз в количествах соответственно a₁, …, a_m единиц. Имеющийся груз необходимо доставить потребителям B₁, …, B_n, спрос которых выражается величинами b₁, …, b_n единиц. Известна стоимость c_ij перевозки единицы груза из i-го пункта отправления в j-й пункт назначения. Удельные транспортные издержки (расходы) записывают в форме матрицы , которую называют матрицей тарифов. Требуется спланировать перевозки, т.е. указать, сколько единиц груза должно быть отправлено от i-го поставщика j-му потребителю, так, чтобы максимально удовлетворить спрос потребителей и чтобы суммарные транспортные затраты на перевозки были при этом минимальными. Рассмотрим простейший случай, когда суммарные запасы поставщиков равны суммарным потребностям

Для составления математической модели задачи введем переменные x_ij , обозначающие количество единиц груза, которые необходимо доставить из i-го пункта отправления в j-й пункт назначения. Все эти переменные можно записать в виде матрицы , которая будет называться матрицей перевозок:

.

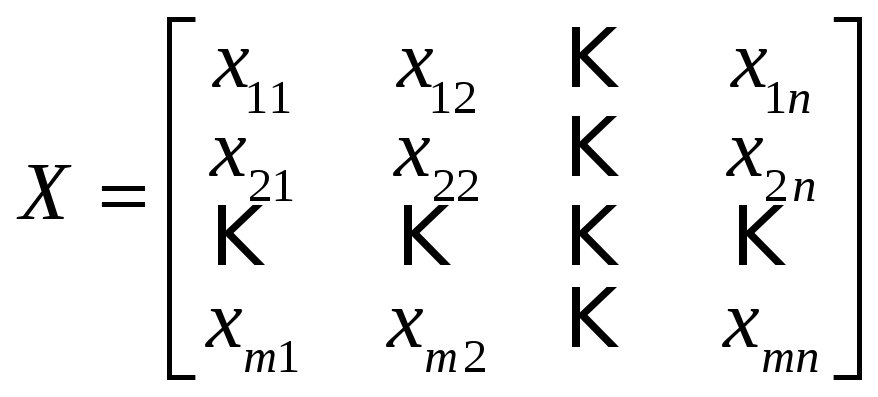Цель транспортной задачи – минимизировать общие затраты на реализацию плана перевозок, которые можно представить целевой функцией:

. (17.1.1.)

Переменные должны удовлетворять следующим условиям:

1) ограничения по запасам:

(17.1.2.)

2) ограничения по потребностям:

(17.1.3.)

3) условия неотрицательности:

x_ij 0 . (17.1.4.)

где c_ij – стоимость перевозки единицы груза из i-го пункта отправления в j-й пункт назначения;

- количество груза, сосредоточенного в пункте ;

- количество груза, необходимое для доставки потребителю .

Если план перевозок удовлетворяет ограничениям (17.1.2) – (17.1.4.), то такой план называется допустимым. Допустимый план перевозок, доставляющий минимум целевой функции называется оптимальным. В следующей теореме, которую примем без доказательства, введем критерий существования допустимого плана.