
Практикум по электричеству / LAB11
.pdf
Б.Н. Сипливый, В.К. Михайлов,
В.В. Подгорный, П.И. Поленичкин.
Практикум по электричеству
Лабораторная работа №11
Собственные колебания в контуре
Целью работы является экспериментальное определение характеристик собственных колебаний в колебательном контуре с помощью осциллографа.
Рассмотрим
Рис.6.1.1. Колебательный контур
6.1.1. Колебательный контур
электрическую цепь, состоящую из последовательно соединенных катушки индуктивности L, конденсатора C и сопротивления R (рис.6.1.1). Если создать первоначальный ток i0 в индуктивности и (или) зарядить конденсатор до некоторого напряжения u0, а затем замкнуть цепь, то в контуре будет происходить свободный (переходный) процесс. Пусть i(t)
— ток в контуре, а u(t) — напряжение на конденсаторе. В соответствии со вторым правилом Кирхгоффа для всех моментов времени t 0 после замыкания ключа в замкнутом контуре (см. рис.6.1.1) имеем:
L di Ri u 0 dt
Поскольку i=dq/dt, а u=q/C , где q — заряд конденсатора, получаем:
|
d2q |
|
dq |
|
q |
|
(1) |
|
L dt2 |
R dt |
|
C |
0 |
||||
|
||||||||
Заменой q=C u, а также дифференцированием (1) можно получить еще два аналогичных уравнения:
|
d2u |
|
du |
|
|
u |
|
(2) |
||||
L dt2 |
R dt |
|
|
C |
0 |
|||||||
|
|
|||||||||||
|
d2i |
|
|
di |
|
|
|
i |
|
|
(3) |
|
L dt2 |
R dt |
|
C |
0 |
||||||||
|
||||||||||||
Дифференциальные уравнения второго порядка (1)-(3) описывают характер изменения заряда и напряжения на конденсаторе и тока в контуре при отсутствии источника внешней ЭДС. Так как эти уравнения абсолютно эквивалентны, рассмотрим, например, второе. Введем обозначения:
02 1/(LC); |
2 R/L, |
(4) |
||||
тогда (2) примет вид: |
|
|
|
|
|
|
|
d 2u |
2 |
du |
2u 0. |
(5) |
|
|
dt2 |
|
||||
|
|
dt |
0 |
|
||
Величина 02 называется собственной частотой колебательной системы без затухания, а — коэффициентом затухания.
Характеристическое уравнение для уравнения (5):
p2 2 p 02 |
0 |
(6) |
Из теории обыкновенных дифференциальных уравнений известно, что возможны три вида решения уравнения (5) в зависимости от вида корней характеристического уравнения (6).
Случай 1. 0 (колебательный процесс). Корни характеристического уравнения: p1, 2 = j , где  20 2 — частота колебаний. Общее решение (5) имеет вид:
20 2 — частота колебаний. Общее решение (5) имеет вид:
u(t) A1 sin( t) A2 cos( t) exp( t) |
(7) |

2
Постоянные интегрирования A1 и A2 определяются начальными условиями, например, током в контуре и напряжением на конденсаторе при t=0. Решение (7) можно переписать в эквивалентном виде:
u(t) A0 exp( t) sin( t ) , |
(8) |
где постоянные А0 и также определяются начальными условиями ( — начальная фаза колебания).
Кривая u(t), представляемая формулой (8), вообще говоря, не периодична, однако величина u периодически и бесконечное число раз проходит через ноль. На рис.6.1.2 показана кривая u(t) при u(0)=0, i(0)=i0. Процессы, описываемые (8), называются затухающими колебаниями. Величина
|
T |
2 |
|
|
2 |
(9) |
||
|
|
|
|
|
|
|||
Рис.6.1.2. Затухающие ко- |
|
|
02 |
2 |
|
|||
называется периодом затухающих |
колебаний |
(термин "период" |
||||||
лебания |
здесь следует понимать условно). Множитель |
|
||||||
|
|
|||||||
|
A(t)=A0 exp( t) |
(10) |
||||||
в (8) перед периодической функцией называется амплитудой затухающих колебаний. Из рис.6.1.2 видно, что амплитуда затухающих колебаний с течением времени уменьшается пропорционально exp( t). Время , за которое амплитуда убывает в e раз, называется временем релаксации. Таким образом, с учетом (10) время релаксации:
|
A(t) |
|
e |
|
exp( t) |
exp( ) , |
|||
|
|
|
exp[ (t )] |
||||||
|
A(t ) |
|
|
|
|||||
следовательно: |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
Логарифм отношения двух взятых через период амплитуд: |
|||||||||
|
ln |
|
A(t) |
|
ln |
exp( t) |
|
T |
|
|
|
|
|
exp[ (t T)] |
|||||
|
|
A(t T) |
|
||||||
называется логарифмическим декрементом затухания .
Важнейшей характеристикой контура является его добротность Q, которая определяется соотношением:
Q= .
Чем меньше декремент затухания , тем выше добротность Q колебательного контура и наоборот, низкая добротность соответствует большому затуханию в контуре. При слабом затухании ( 0) с учетом обозначений (9) и (4):
Q |
|
|
02 2 |
|
0 |
|
1 |
|
|
L |
|
. |
T |
2 |
2 |
|
|
||||||||
|
|
|
|
R C |
||||||||
Случай 2. 0 (критическая частота). Корни характеристического уравнения: p1, 2= . Из условия 0 с учетом (4) определяется величина критического сопротивления R контура:
|
Rcr 05. |
|
L/ C |
|
(11) |
Общее решение (5) имеет вид: |
|
|
|
|
|
|
u(t) A1 A2t exp( t) , |
|
|||
|
где постоянные А1 и А2 определяются из начальных условий зада- |
||||
|
чи. В зависимости от значений постоянных интегрирования А1 и |
||||
|
А2 величина u будет |
или не будет проходить |
через максимум |
||
|
(рис.6.1.3). Но в любом случае при t u(t) асимптотически при- |
||||
|
ближается к нулю и процесс не будет колебательным. |
||||
|
Случай 3. 0 (апериодический процесс). Корни характе- |
||||
Рис.6.1.3. Апериодиче- |
ристического уравнения: p1, 2= , где 2 |
2 02. Общее |
|||
ские процессы |
решение уравнения (5) имеет вид: |
|
|||
|
|
3 |
|
u(t) A1sh( t) A2ch( t) exp( t) . |
(12) |
Постоянные A1 и A2 здесь также определяются из начальных условий. Как и в предыдущем |
||
варианте, процесс, описываемый соотношением (12), является апериодическим. |
|
|
|
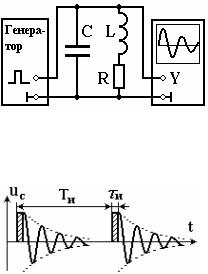
6.1.2. Лабораторная установка |
|
|
Схема установки для наблюдения и исследования соб- |
|
|
ственных колебаний изображена на рис.6.1.4. Емкость C, ин- |
|
|
дуктивность L и сопротивление R образуют колебательный |
|
|
контур. Катушка индуктивности выполнена в виде соленои- |
|
|
да. Емкость C задается переключателями на магазине емко- |
|
|
сти. Сопротивление R образуют проволока катушки индук- |
|
Рис.6.1.4. Схема установки |
тивности и подводящие провода (R0), а также магазин сопро- |
|
тивления, т.е. R=R0+Rмаг. Колебания в контуре наблюдаются |
||
на экране осциллографа. Для возбуждения колебаний служит генератор импульсов, который выдает прямоугольные импульсы амплитудой 5-10 В, длительностью и = 1 мкс и частотой = 1 кГц. Длительность импульсов выбирается такой, чтобы за время и конденсатор успел зарядиться, а период их повторения Tи=1/ должен быть много больше периода колебаний T в контуре (9), так чтобы между двумя импульсами генератора колебания в контуре ус-
Рис.6.1.5. Возбуждение коле- пели почти полностью затухнуть (рис.6.1.5).
баний
6.1.3. Программа работы
1.Собрать элементы в схему, показанную на рис.6.1.4. Исходные положения регулировок передней панели осциллографа следующие. Синхронизация — внутренняя. Развертка
—автоматическая, 50 мкс/дел. Усиление по Y — 0,1- 0,2 В/дел . Яркость - средняя. Генератор импульсов настроен на требуемый режим и никаким регулировкам во время выполнения работы не подлежит.
2.Включить генератор импульсов и осциллограф и дать им прогреться 2-3 мин. На магазине емкости выставить C=1 мкФ, на магазине сопротивления — 0. Плавными регулировками яркости, фокуса и уровня синхронизации добиться умеренно яркой и четкой картины затухающих колебаний на экране осциллографа. Переключателем усиления по Y добиться максимального разрешения колебаний по амплитуде, а длительность развертки установить такой, чтобы на экране умещалось 6-10 полных колебаний.
3.По картине колебаний определить их период Т и логарифмический декремент зату-
хания . При измерениях для уменьшения погрешности измерений необходимо по возможности использовать всю шкалу осциллографа.
4.Измерить период колебаний и определить логарифмический декремент затухания еще для двух значений емкости, например, для С=0,3 и С=0,1 мкФ при Rмаг =0.
5.Увеличивая сопротивление магазина Rмаг при С =1 мкФ, проследить за возрастани-
ем скорости затухания и переходом колебательного процесса в апериодический. Измерить периоды колебаний и определить логарифмические декременты затухания для двух значений Rмаг, например, для 1 и 2 0м. Найти критическое сопротивление Rкрмаг , при котором процесс становится апериодическим.
6.1.4.Обработка результатов
1.По результатам п.3 раздела 6.1.3, т.е. по измеренным T и вычислить общее активное сопротивление соленоида и соединительных проводов R0 , а также индуктивность L соленоида. Полученное значение L сопоставить с результатом вычисления индуктивности соленоида в приближении его бесконечной длины.
4
2.По результатам измерений периодов затухающих колебаний в контуре при С =1 и 0,1 мкФ и R=R0 вычислить их частоты и оценить, насколько увеличились бы эти частоты при нулевом сопротивлении всех проводов, т.е. при R0=0.
3.Определить добротности контура для трех случаев: (C=1 мкФ, R=R0), (C=0,1 мкФ, R=R0), (C=1 мкФ, R=R0+Rмаг).
4.Рассчитать критическое сопротивление Rкр (11) для С=1 мкФ и сопоставить его с
экспериментальным значением R0+Rкрмаг.
6.1.5.Контрольные вопросы и задания
1.Вывести уравнение собственных затухающих колебаний в контуре и получить его решения для различных коэффициентов затухания.
2.Дать определения времени релаксации, логарифмического декремента затухания, добротности контура, критического сопротивления.
3.При какой добротности контура колебательный процесс в нем переходит в апериодический?
4.Определить добротность контура, частота колебаний в котором 0 .
5.Рассчитать число полных колебаний в RLC контуре, после которых амплитуда уменьшится в N раз.
6.Вывести формулу для расчета индуктивности соленоида.
6.1.6.Литература
1.Р.С. Гутер, А.Р. Янпольский. Дифференциальные уравнения. М.: Высшая школа, 1976, § 15.
2.С.Г. Калашников. Электричество. М.: Наука, 1985, §§ 207-210, 81.
