
Михайлов Аналитическая геометрия 2008
.pdf
и прямой
x x1 |
|
y y1 |
|
z z1 |
(7.16) |
l |
|
m |
|
n |
|
|
|
|
Определяется как дополнительный к углу между нормальным
|
|
|
|
|
|
|
|
|
|
|
|
A, B, C |
|
|
и направляющим вектором |
|||||||||||||||
вектором плоскости n |
|
|
|
|
|
|||||||||||||||||||||||||
прямой |
|
|
l, m, n . Если угол между векторами обозначить |
|||||||||||||||||||||||||||
q |
|
|||||||||||||||||||||||||||||
, а угол меду прямой и плоскостью |
|
, то |
2 |
. |
||||||||||||||||||||||||||
Следовательно: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
A l |
|
B m |
|
|
C n |
|
|
|
|
|
|
|
||||||||||
cos |
|
n q |
|
|
|
|
|
|
|
|
|
|
|
sin |
. (7.17) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
n |
|
q |
|
|
A |
2 |
B |
2 |
|
C |
2 |
|
|
|
|
l |
2 |
m |
2 |
n |
2 |
|
|
|
|
|||
Условие перпендикулярности векторов |
|
|
|
|
|
|||||||||||||||||||||||||
n |
и q |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
A l |
|
|
B m |
C n |
0 |
|
|
(7.18) |
|||||||||||
|
|
|
|
|
|
|
n q |
|
|
|
|
|
|
|||||||||||||||||
соответствует параллельности прямой и плоскости, а условие |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
парллельности векторов n |
и q |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
A |
|
B |
|
|
C |
|
|
|
|
|
|
|
(7.19) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
l |
|
m |
|
|
|
n |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
означает перпендикулярность прямой и плоскости.
Для того, чтобы прямая (7.16) принадлежала плоскости (7.15) должны быть выполнены два условия:
1. условие параллельности прямой и плоскости
A l B m |
C n 0 |
(7.20) |
2. координаты точки M1 |
x1, y1, z1 |
, принадлежащей |
прямой, должны обращать уравнение плоскости в тождество
A x1 B y1 C z1 D 0 |
(7.21) |
Для того, чтобы две прямые (7.22) и (7.23) принадлежали
x |
x1 |
|
|
|
y |
y1 |
|
z |
z1 |
|
(7.22) |
||
|
l1 |
|
|
|
|
m1 |
|
n1 |
|||||
|
|
|
|
|
|
|
|||||||
x |
x2 |
|
|
|
y |
y2 |
|
|
z |
z21 |
(7.23) |
||
|
l2 |
|
|
|
|
m2 |
|
|
n2 |
||||
|
|
|
|
|
|
|
|
||||||
71

одной плоскости необходимо и достаточно, чтобы три вектора
|
|
l2 , m2 , n2 и |
q1 |
l1, m1, n1 q2 |
|
M1M 2 |
x2 x1 , y2 |
y1 , z2 z1 |
были компланарны.
Приравняв нулю смешанное произведение этих векторов, получим условие принадлежности двух прямых к одной плоскости.
|
|
x2 |
x1 |
y2 y1 |
z2 |
z1 |
|
|
l1 |
m1 |
n1 |
|
|
||
M1M 2 q1 |
q2 |
|
|
0 (7.24) |
|||
|
|
|
l2 |
m2 |
n2 |
|
|
Задачи № 983, 985, 991, 1003, 1005, 1007, 1009, 1012, 1018,
1024, 1029, 1030.
§8. Основные задачи на прямую и плоскость в пространстве
Задача 8.1.
Найти точку пересечения прямой
|
|
x |
x1 |
|
|
y |
y1 |
|
|
z |
z1 |
|
(8.1) |
||||
|
|
|
l |
|
|
|
|
m |
|
|
|
|
|
n |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
И плоскости |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Ax |
|
Dy Cz |
D |
0 |
|
(8.2) |
|||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Приравняем выражение (8.1) к параметру t |
и выразим через |
||||||||||||||||
него x, y и z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x x1 |
|
|
y |
|
y1 |
|
|
z |
|
z1 |
t |
(8.3) |
||||
|
l |
|
|
|
m |
|
|
|
n |
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
x |
|
x1 |
l |
t |
|
|
|
|||||
|
|
|
|
y |
|
y1 |
m |
t |
|
|
(8.4) |
||||||
|
|
|
|
|
z |
|
z1 |
n |
t |
|
|
|
|||||
72

Подставим x, y и z из (8.4) в уравнение плоскости.
A x1 l t B y1 m t C z1 n t D 0 |
(8.5) |
Координаты точки пересечения прямой и плоскости получим, подставив значение t0 , найденное из (8.5) в уравнения (8.4).
x0 |
x1 |
l |
t0 |
|
y0 |
y1 |
m |
t0 |
(8.6) |
z0 |
z1 |
n |
t0 |
|
Задача 8.2.
Составить уравнение плоскости, проходящей через точку M 2 x2 , y2 , z2 и прямую (8.7)
x x1 |
|
y y1 |
|
z z1 |
(8.7) |
l |
|
m |
|
n |
|
|
|
|
Решение.
Положение искомой плоскости определяют два вектора: направляющий вектор прямой
|
|
l, m, n |
|
|
|
|
q |
|
|
|
|
и вектор |
|
|
|
|
|
M1M 2 |
x2 |
x1 , y2 |
y1 , z2 |
z1 , |
|
точка начала которого |
M1 x1, y1, z1 |
принадлежит прямой. |
|||
Введем в рассмотрение «свободный вектор» |
|||||
M1M |
x x1 , y y1 , z z1 |
, |
|||
конечная точка которого M x, |
y, z |
−. |
произвольная точка |
||
пространства.
Чтобы эта точка принадлежала искомой плоскости, необходимо и достаточно, чтобы три рассматриваемые вектора были компланарны, а их смешанное произведение равнялось нулю. Исходя из этого, запишем уравнение искомой плоскости в матричной форме:
73

|
x |
x1 |
y |
y1 |
z |
z |
|
|
|
|
|
|
|
|
|
M1M M1M 2 q |
x2 |
x1 |
y2 |
y1 |
z2 |
z1 |
0 (8.8) |
|
|
l |
|
m |
|
n |
|
|
|
|
|
|
|
|
|
Частным случаем рассмотренной задачи является задача о плоскости, проходящей через две параллельные прямые. В этом случае точка M 2 x2 , y2 , z2 берется со второй прямой
x |
x1 |
|
|
|
y |
y1 |
|
z |
z1 |
|
||
|
l1 |
|
|
|
|
m1 |
|
n1 |
||||
x |
x2 |
|
|
|
y |
y2 |
|
|
z |
z21 |
||
|
l1 |
|
|
|
|
m1 |
|
|
n1 |
|||
и ход решения повторяется.
Задача 8.3.
Составить уравнение плоскости, проходящей скрещивающихся прямых параллельно второй.
(8.9)
(8.10)
через одну из
x |
x1 |
|
|
|
y |
y1 |
|
z |
z1 |
|
(8.11) |
||
|
l1 |
|
|
|
|
m1 |
|
n1 |
|||||
|
|
|
|
|
|
|
|||||||
x |
x2 |
|
|
|
y |
y2 |
|
|
z |
z21 |
(8.12) |
||
|
l2 |
|
|
|
|
m2 |
|
|
n2 |
||||
|
|
|
|
|
|
|
|
||||||
Решение.
Ориентацию в пространстве искомой плоскости определяют
направляющие вектора прямых |
|
||
|
|
|
|
q1 |
l1, m1 , n1 |
è q2 |
l2 , m2 , n2 |
Введем в рассмотрение «свободный вектор» |
|||
M1M |
x x1 , y y1 , z z1 , |
||
конечная точка |
которого |
M x, y, z −.произвольная точка |
|
пространства, а начальная точка M1 |
x1, y1, z1 взята с первой |
||
прямой. |
|
|
|
Из условия |
компланарности рассматриваемых векторов |
||
запишем уравнение искомой плоскости в матричной форме.
74
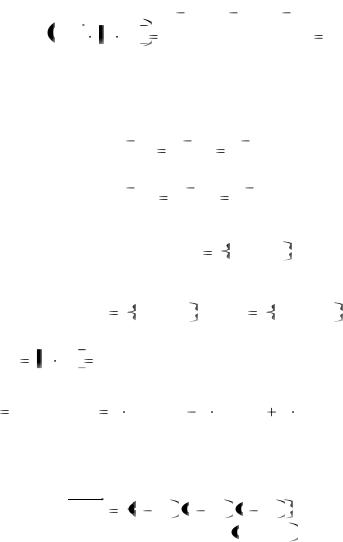
|
|
x |
x1 |
y y1 |
z z1 |
|
|
|
|
|
|
|
|
||
M1M q1 |
q2 |
|
l1 |
m1 |
n1 |
0 . |
(8.13) |
|
|
|
l2 |
m2 |
n2 |
|
|
Задача 8.4.
Составить уравнение общего перпендикуляра двух скрещивающихся прямых
x |
x1 |
|
|
|
y |
y1 |
|
z |
z1 |
|
(8.14) |
||
|
l1 |
|
|
|
|
m1 |
|
n1 |
|||||
|
|
|
|
|
|
|
|||||||
x |
x2 |
|
|
|
y |
y2 |
|
|
z |
z21 |
(8.15) |
||
|
l2 |
|
|
|
|
m2 |
|
|
n2 |
||||
|
|
|
|
|
|
|
|
||||||
Решение.
Направляющий вектор q3 l3 , m3 , n3 искомой прямой
вычисляем как векторное произведение направляющих векторов заданных прямых
|
|
|
|
|
|
|
|
|
|
|
q1 |
l1, m1 , n1 |
è q2 |
l2 , m2 , n2 |
|
|
|
|
|
|
|
|
|
|
||
Так как по условиям задачи |
q3 |
перпендикулярен |
q1 |
и q2 . |
||||
|
|
|
|
|
|
|
|
|
q3 |
q1 |
q2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
i |
j |
k |
|
|
|
m |
n |
|
|
|
l |
n |
|
|
|
l |
m |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
l1 |
m1 |
n1 |
|
i |
|
1 |
1 |
|
j |
|
|
1 |
1 |
|
k |
|
1 |
1 |
(8.16) |
|
|
|
m2 |
n2 |
|
|
|
l2 |
n2 |
|
|
l2 |
m2 |
|||||||
|
l2 |
m2 |
n2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Из условия компланарности векторов |
q1 |
, |
q3 |
и свободного |
||||||||||||||||
вектора |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
M1M |
|
x x1 , y y1 , z z1 |
, |
|
|
|
|
||||||||||
начальная |
точка |
|
которого |
|
M1 |
x1, y1, z1 |
|
взята с первой |
||||||||||||
прямой, запишем в матричной форме уравнение плоскости,
проходящей через первую прямую параллельно вектору q3 .
75

|
|
x |
x1 y |
y1 z |
z1 |
|
|
|
|
|
|
|
|
|
|
||
M1M q1 |
q3 |
l1 |
|
m1 |
n1 |
0 . |
|
(8.17) |
|
|
l3 |
|
m3 |
n3 |
|
|
|
|
|
|
|
|
|
|
||
Аналогично, из условия компланарности векторов |
q |
2 , q3 и |
||||||
свободного вектора |
|
|
|
|
|
|
|
|
M 2 M |
x x2 , y y2 , z z2 |
, |
|
|
|
|||
начальная точка |
которого |
M 2 |
x2 , y2 , z2 |
взята со |
второй |
|||
прямой, запишем в матричной форме уравнение плоскости,
|
|
|
|
|
|
|
|
проходящей через вторую прямую параллельно вектору q3 . |
|||||||
|
|
x |
x1 |
y y1 |
z z1 |
|
|
|
|
|
|
|
|
||
M 2 M q1 |
q3 |
|
l2 |
m2 |
n2 |
0 . |
(8.18) |
|
|
|
l3 |
m3 |
n3 |
|
|
Линия пересечения этих плоскостей и есть искомый общий
перпендикуляр. |
|
|
|
Чтобы получить искомый общий |
перпендикуляр |
в |
|
каноническом виде можно |
найти точку M 0 x0 , y0 , z0 |
в |
|
которой пересекается вторая |
прямая с |
плоскостью (8.17). |
|
(Способ нахождения этой точки рассмотрен в задаче 8.1) и записать каноническое уравнение прямой, проходящей через
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
точку M 0 |
с направляющим вектором q3 . |
|
|
|
||||||||||||||
|
|
x |
x0 |
|
|
y |
y0 |
|
|
z |
z0 |
|
|
|
(8.19) |
|||
|
|
l3 |
|
|
|
|
|
m3 |
|
|
|
n3 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Задача 8.5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Составить |
уравнение |
прямой, проходящей через точку |
||||||||||||||||
M 3 x2 , y3 , z3 |
и |
|
|
пересекающейся |
с |
каждой |
из |
|||||||||||
скрещивающихся прямых (8.20) и (8.21) |
|
|
|
|||||||||||||||
|
|
x |
x1 |
|
|
|
y |
y1 |
|
|
z |
z1 |
|
|
|
(8.20) |
||
|
|
l1 |
|
|
|
|
|
m1 |
|
|
n1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
76

|
x |
x2 |
|
|
y y2 |
|
z |
z2 |
(8.21) |
|
|
l2 |
|
|
m2 |
|
|
n2 |
|
|
|
|
|
|
|
|
|||
Решение. |
|
|
|
|
|
|
|
|
|
Через точку M 3 |
и |
каждую |
из |
прямых можно провести |
|||||
плоскость (задача 8.2). Линия пересечения этих плоскостей и есть искомая прямая.
Задачи № 1039, 1044, 1050, 1052, 1066, 1071, 1072, 1078,
1083.
§9. Кривые второго порядка 9.1. Эллипс
Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до двух точек F1 и F2 , называе-
мых фокусами, есть величина постоянная.
Если фокусы совпадают, то эллипс превращается в окружность.
y
|
|
M x, y |
|
|
|
r1 |
|
|
|
r2 |
|
|
|
|
|
|
|
|
x |
F1 c,0 |
0 |
F2 c,0 |
|
|
|||
Рис. 9.1
Ось Ox проведем через точки F1 и F2 , начало координат поместим в среднюю точку отрезка F1 F2 . Расстояние между и фокусами примем за 2c , Обозначим через r1 и r2 длины отрезков F1 M и F2 M . Пусть r1 r2 2a , тогда a c .
77

r |
x |
c 2 |
y 2 |
r |
x |
c 2 |
y 2 |
(9.1) |
||
1 |
|
|
|
|
2 |
|
|
|
|
|
В соответствии с определением эллипса: |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
c 2 |
y 2 |
|
x |
c 2 |
y 2 |
2a |
(9.2) |
|
Это уже уравнение эллипса. С помощью стандартного приѐма уничтожения радикалов оно приводится к каноническому виду
|
|
x 2 |
|
y 2 |
1 |
, |
(9.3) |
|
|
a 2 |
|
b2 |
|||
|
|
|
|
|
|
||
где |
b2 a2 c2 . |
|
|
|
|
|
|
Величины a и b называются большой и малой полуосями эллипса. Координаты точек пересечения эллипса с осями координат
x  a и y
a и y  b ,
b ,
легко получить, подставив в уравнение (9.3) уравнения осей координат y 0 и x 0.
Графическое изображение эллипса представлено на рис. 9.2.
b
a |
a |
b
Рис. 9.2
9.2. Гипербола.
Гиперболой называется геометрическое место точек плоскости, для которых модуль разности расстояний до двух
78

фиксированных точек F1 и F2 , называемых фокусами, есть величина постоянная.
|
Обозначим через r1 и r2 |
длины отрезков F1 M и F2 M . Пусть |
||
|
r1 r2 |
|
2a , тогда будет a |
c . |
|
|
|||
Систему координат выберем так же, как при выводе уравнения эллипса (рис. 9.1). Согласно определению гиперболы, еѐ уравнение будет иметь следующий вид:
|
|
x c 2 y 2 |
|
|
|
|
x |
c 2 |
y 2 |
2a |
(9.4) |
||
С помощью стандартного приѐма уничтожения радикалов оно |
|||||||||||||
приводится к каноническому виду: |
|
|
|
|
|
||||||||
|
|
|
x 2 |
|
y 2 |
|
1 |
, |
|
|
(9.5) |
||
|
|
|
a 2 |
b2 |
|
|
|||||||
|
|
|
|
|
|
|
|
||||||
где b2 c2 a2 . |
|
|
|
|
|
|
|
|
|||||
Гипербола пересекает ось Ox в точках x |
a и x |
a , в чем |
|||||||||||
легко убедиться, подставив в уравнение гиперболы (9.5) уравнение оси Ox - y 0 . Получим уравнение
|
x 2 |
1 |
|
||
|
a 2 |
|
|||
|
|
|
|
|
|
решения которого имеют вид x |
a и x |
a |
|||
Асимптотами гиперболы являются прямые с уравнениями |
|||||
Y |
|
b |
x . |
(9.6) |
|
|
|
||||
|
|
|
a |
|
|
Чтобы убедиться в этом, получим из уравнения (9.5) явное выражение для y :
|
b |
|
|
|
|
|
|
y |
|
x2 |
a2 |
(9.7) |
|||
|
|
||||||
a |
|||||||
|
|
|
|
|
|
||
и рассмотрим поведение разности Y |
y при x |
. |
|||||
79

b |
|
|
|
|
|
|
b |
lim |
x 2 |
x 2 |
a 2 |
|||||||||
lim x |
x 2 a 2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
a x |
|
|
|
|
|
|
a x |
|
x |
x 2 |
a 2 |
|||||||||
|
|
|
b |
lim |
|
|
a 2 |
|
|
|
|
|
0. |
(9.8) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
a x |
|
|
|
|
a |
2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
x 1 |
1 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Утверждение (9.6) доказано.
9.3. Парабола
Параболой называется геометрическое место точек
плоскости, для которых расстояние |
r |
от некоторой точки F , |
||||||
именуемой фокусом, равно расстоянию |
d |
до некоторой прямой, |
||||||
именуемой директрисой. |
|
|
|
|
||||
Для вывода уравнения параболы точку F поместим на оси Ox |
||||||||
на расстоянии, равном |
p |
вправо от начала координат, а |
||||||
|
|
|||||||
2 |
|
|
|
|
|
|
||
директрису проведем параллельно оси |
Oy на таком же расстоянии |
|||||||
влево от начала координат (Рис.9.3.) |
|
|
|
|
||||
|
|
|
y |
|
|
|
|
|
|
|
|
d |
|
M x, y |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
F |
p |
,0 |
|
||
|
|
|
|
|
|
2 |
|
|
p
2Рис. 9.3
Всоответствии с определением параболы
80
