Добавил:

fench Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский ядерный университет (МИФИ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Михайлов Аналитическая геометрия 2008

.pdf

Скачиваний:

Добавлен:

16.08.2013

Размер:

1.81 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 97 8 9 > Следующая >>>

Косинус угла между векторами можно найти исходя из определения скалярного произведения

cos

B1 B2

. (6.8)

A12

B12

C12

A22

B22 C22

Условие ортогональности плоскостей следует из условия ортогональности их нормальных векторов, то есть равенства нулю их скалярного произведения:

			A1 A2 B1 B2 C1 C2 0 . (6.9)
n1	n2	0	A1 A2 B1 B2 C1 C2 0 . (6.9)

Условия параллельности плоскостей следуют из условия коллинеарности их нормальных векторов:

			A1	B1		C1		.		(6.10)

			A2	B2		C2
Задача 6.1. Составить уравнение плоскости, проходящей
через три заданные точки.
Пусть заданы точки
M1 x1 , y1 , z1 M 2 x2 , y2 , z2								M 3 x3 , y3 , z3 ,
не принадлежащие одной прямой. Тогда вектора
M1M 2	x2	x1; y2	y1; z2		z1		и
M1M 3	x3	x1; y3	y1; z3		z1
не будут коллинеарными. Пусть точка M x, y, z										«свободная
точка» с произвольными координатами x, y, z , а вектор
M1M x x1; y y1; z z1
«свободный вектор». Чтобы точка							M x,		y, z принадлежала
плоскости,	определяемой			векторами					M1M 2	и M1M 3

необходимо и достаточно, чтобы все три вектора были компланарны, а их смешанное произведение равнялось нулю.

	x	x1	y	y1	z	z1
M1 M M 1 M 2 M1 M 3	x2	x1	y2	y1	z2	z1	0 (6.11)
	x3	x1	y3	y1	z3	z1

Нормальное уравнение плоскости. Отклонение точки от плоскости.

Рассмотрим плоскость 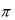(рис 6.3). Из начала координат проведем нормаль к этой плоскости. Точку пересечения нормали с плоскостью обозначим P . Величину отрезка


OP обозначим p . Орт нормали OP обозначим en .

	en	cos		; cos	; cos
Чтобы	свободная			точка		M x, y, z		принадлежала
плоскости	, необходимо и достаточно чтобы проекция
радиуса-вектора OM				x 0, y		0, z	0	x, y, z	точки M
на нормаль OP равнялась числу p .

Ïð n OM	OM	en	x cos		y cos		z cos	p	(6.12)
Нормальное уравнение плоскости получим, если в (6.12)
перенесем влево от знака равенства число p .
	x cos			y cos		z cos	p	0	(6.13)

Отклонение точки от плоскости.

Пусть число d PQ − расстояние от точки M 0 x0 , y0 , zo до

плоскости. Отклонение точки от плоскости d , если точка и начало координат лежат по разные стороны от плоскости, и d , если точка и начало координат лежат по одну сторону от плоскости.

PQ OQ p	x0 cos	y0 cos	z0 cos	p	(6.14)
Здесь

OQ Ïð n OM 0	en OM 0	x0 cos	y0 cos	z0 cos	(6.15)

z	Q
	Q
		M 0
P			y
P			y

	M
O
Рис. 6.3	x
Рис. 6.3

Нормальное уравнение плоскости
x cos	y cos	z	cos	p 0	(6.13)
и общее уравнение плоскости
A x B y	C z	D	0		(6.1)

определяют одну и ту же плоскость, следовательно

существует такое число				, что
A	cos ,	B cos ,			C	cos	,	D p (6.16)
cos2	cos2		cos2	1	2	A2	B 2	C 2
				1				(6.17)


			A2	B 2	C 2

Из четвертого равенства выражения (6.16) следует, что знак

противоположен знаку D . Число 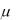называется

нормирующим множителем. Для получения нормального уравнения плоскости достаточно умножить общее уравнение на нормирующий множитель .

Отклонение точки от плоскости			получим,	подставив
координаты точки M 0	x0 , y0 в уравнение (6.14).
Определение 6.1. Множество плоскостей, пересе-
кающихс по одной прямой L , называется пучком плоскостей
Теорема 5.3. Уравнение
A1x B1 y C1z D1	A2 x	B2 y	C2 z D2	0 (6.18)
есть уравнение пучка плоскостей, если				и	не
обращаются в нуль одновременно, а уравнения
A1 x B1 y C1 z D1	0 и A2 x	B2 y	C2 z D2	0	(6.19)

суть уравнения двух плоскостей, пересекающихся по прямой L . Любая плоскость, проходящая через прямую L , определяется уравнением (6.19) при некоторых значениях чисел и .

Доказательство. Преобразуем уравнение к следующему виду:

A1	A2 x	B1	B2	y	(6.20)
C1	C2 z	D1	D2 0

Это уравнение плоскости, если выражения в скобках не равны нулю одновременно. Предположим противное. Тогда, из

A2 0

следует

из

следует

из

следует

В итоге

(6.21)

Это условие параллельности плоскостей (6.19), что противоречит условиям теоремы. Тем самым доказано, что уравнение (6.18) всегда определяет некоторую плоскость.

Покажем, что любая плоскость, принадлежащая пучку определяется уравнением (6.18) при некоторых значениях

чисел	и	. Фиксируем	точку	M1 x1, y1, z1 ,	не
принадлежащую		прямой L .	Точка	M1 и прямая	L

определяют плоскость, принадлежащую пучку, единственным образом.

Подставив координаты точки M1 в уравнение		(6.18),
получим уравнение относительно неизвестных и .
A1x1 B1 y1 C1z1 D1	A2 x1 B2 y1 C2 z1 D2	0

В этом уравнении выражения в круглых скобках не могут обратиться в нуль одновременно, так как точка M1 не может

принадлежать двум различным плоскостям (6.19). Пусть

A1x1 B1 y1 C1z1 D1 0 ,

Тогда

	A2 x1	B2 y1	C2 z1	D2	(6.22)
	A1 x1	B1 y1	C1 z1	D

Из (6.22) значения		и определяются с точностью до

произвольного общего множителя.

Можно представить уравнение пучка плоскостей в другом

виде, разделив (6.18) на		и положив		:
виде, разделив (6.18) на		и положив		:
A1x B1 y C1z D1		A2 x B2 y	C2 z	D2	0 (6.23)
Типовые задачи.
Задача 6.2.
Дана плоскость	A1 x	B1 y C1 z D1	0	и	точка

M 0 x0 , y0 , z0 .

Составить уравнение плоскости, походящей через данную точку параллельно заданной плоскости.

Решение.


Нормальный вектор заданной плоскости n1									A1 , B1	,C1 , он
же будет нормальным вектором искомой плоскости.
Чтобы «свободная точка»				M x, y, z принадлежала искомой
плоскости,	вектор	M 0 M		x	x0 ,	y	y0 ,	z	z0	должен

быть перпендикулярен			вектору			n1 .	Условие перпен-
дикулярности векторов

n1 M 0 M	A1 x	x0	B1	y	y0	C1	z	z1	0	(6.24)

есть искомое уравнение. Раскрыв скобки и введя обозначение

D2 A1 x0	B1 y0	C1 z0	запишем		найденное		уравнение в
общем виде
	A1 x B1 y C2 z				D2	0	(6.25)
Задача 6.3.
Задано уравнение пучка плоскостей
A1x B1 y	C1z	D1	A2 x	B2 y		C2 z D2	0 , (6.26)
и плоскость	3
	A3 x	B3 y	C3 z	D3	0 .		(6.26*)

Составить уравнение плоскости, принадлежащей пучку,

параллельной плоскости			3 .
	Решение. Преобразуем уравнение (6.26)
A1	A2 x B1	B2	y C1 C2 z D1	D2 0 .

Это уравнение искомой плоскости. Его нормальный вектор,

имеющий вид

		n A1	A2 , B1		B2 , C1	C2 ,

параллелен вектору n3			A3 , B3 ,C3 .
Условие параллельности векторов
	A1	A2	B1	B2 C1	C2		(6.27)
		A3	B3		C3		(6.27)
		A3	B3		C3
содержит		единственную		неизвестную		величину	.
Определив число			и подставив его в уравнение (6.26),
получим уравнение искомой плоскости.

Связка плоскостей есть множество плоскостей, имеющих

одну общую точку M 0		x0 , y0 , z0 .	Уравнение		связки
плоскостей имеет вид
A x	x0 B y	y0 C z	z0	0 .	(6.28)
В этом уравнении фиксированы координаты точки					M 0 , а
коэффициенты	A, B, C	произвольные		числа,	не

обращающиеся в нуль одновременно..

Задачи № 913, 919, 920, 927, 931, 942, 946, 952, 961, 964, 973.

§ 7. Прямая линия в трехмерном пространстве

Прямую линию в пространстве можно определить как линию пересечения двух непараллельных плоскостей.

A1 x B1 y	C1 z D1	0
A2 x B2 y	C2 z D2	0 .		(7.1)
Часто удобнее канонический вид уравнения прямой.
Определение 7.1. Любой ненулевой вектор				l, m, n ,
Определение 7.1. Любой ненулевой вектор			q	l, m, n ,

параллельный данной прямой будем называть направляющим вектором прямой.

Задача 7.1. Составить уравнение прямой L , проходящей

через точку M1 x1, y1, z1 параллельно вектору q l, m, n .

Рис. 7.1

Решение.
Рассмотрим вектор M1M	x	x1 ,		y y1 ,	z	z1 , начало
которого совпадает с точкой M1 , а конец − в произвольной
точке M x, y, z .
Чтобы точка M лежала		на	прямой		L ,	вектор M1M
должен быть параллелен вектору				. Условие параллельности
должен быть параллелен вектору			q	. Условие параллельности

векторов состоит в пропорциональности сходственных координат, из чего следует

x x1	y y1	z z1	(7.2)
l	m	n	(7.2)
l	m	n

Это уравнение называется каноническим уравнением прямой в пространстве.

Приравняв выражение (7.2) параметру t , получим

параметрические уравнения прямой.

x	x1	l	t
y	y1	m	t	(7.3)
z	z1	n	t

Эти уравнения имеют наглядное физическое истолкование.
Если принять что,	t −время, а					вектор
		v	i l	j m	k n

скорости, то уравнения (7.3) − это три проекции уравнения движения точки на координатные оси.

Уравнение прямой, проходящей через две заданные

точки M1 x1, y1, z1			и M 2 x2 , y2 , z2				получим из уравнения
(7.2), приняв, что направляющий вектор
								(7.4)
q M1M 2			x2		x1 , y2	y1	, z2 z1
и подставив выражение (7.4) в (7.2):
	x	x1		y	y1	z	z1	(7.5)
	x2	x1		y2	y1	z2	z1

Чтобы привести к каноническому виду уравнение прямой, заданной как линия пересечения двух плоскостей, нужно

найти направляющий вектор прямой и точку, лежащую на прямой. Длина вектора − произвольная, точка, лежащая на прямой − любая.

Пусть прямая есть линия пересечения плоскостей (7.6)

A1 x B1 y C1 z D1

A2 x

B2 y C2 z

0 .

(7.6)

Направляющий вектор прямой q ортогонален каждому из

нармальных векторов плоскостей

A , B ,C

n A , B ,C

и n

Поэтому определим вектор q , как векторное произведение

нормальных векторов

(7.7)

Компоненты вектора q будут иметь вид

(7.8)

;

Для определения координат точки, лежащей на прямой,

добавим в систему уравнений (7.6) уравнение третьей

плоскости. Удобно добавить одну из координатных

плоскостей x

0, y

0 или z

0 .

Чтобы получающаяся система уравнений второго порядка имела единственное решение, еѐ главный определитель не должен обращаться в нуль. Это накладывает ограничения на выбор координатной плоскости.

Пусть z 0 . Пусть в полученной системе уравнений

A1 x	B1 y	D1	0	.	(7.9)
A2 x	B2 y	D2	0

главный определитель	A1	B1	0 .
	A2	B2

Тогда координаты искомой точки определяются по формулам Крамера

; y0

; z0 0 .

(7.10)

Искомое каноническое уравнение запишем в следующем виде

(7.11)

Угол между прямыми, а также условия перпендикулярности и параллельности прямых очевидным образом связаны с соответствующими соотношениями между их

направляющими векторами q .

cos

l1 l2

m1 m2

n1 n2

(7.12)

l12

m12

n12

l22

m22

n22

Условие перпендикулярности двух прямых:

l2 m1 m2

n1 n2

0 .

(7.13)

Условия параллельности прямых:

(7.14)

(Нуль в знаменателе в этой пропорции означает, что соответствующий числитель тоже обращается в нуль.)

Угол между плоскостью

Ax By Cz D 0

(7.15)

<<< < Предыдущая 1 2 3 4 5 67 / 97 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.08.2013841.72 Кб76Медведева Основы теории множеств и теории отображений 2011.pdf
#
16.08.20135.06 Mб151Мелников Газовые лазеры с ядерной накачкой 2008.pdf
#
16.08.20131.12 Mб128Милованов Лабораторный практикум по СВЧ 2007.pdf
#
16.08.201311.87 Mб111Мирнов Енергия из воды 2007.pdf
#
16.08.20131.39 Mб68Мирошин Интегралные и дифференциалные операторы 2010.pdf
#
16.08.20131.81 Mб41Михайлов Аналитическая геометрия 2008.pdf
#
16.08.201314.52 Mб145Михайлов Ултразвуковое исследование сердца-ехокардиография 2011.pdf
#
16.08.20133.52 Mб179Михеев Датчики и детекторы 2007.pdf
#
16.08.20137.61 Mб173Михеев Исполнителные устройства автоматических 2008.pdf
#
16.08.20138.57 Mб193Мишулина Лабораторный практикум по курсу 2007.pdf
#
16.08.20133.86 Mб115Мишулина Основы теории вероятностей 2011.pdf