Жданов Тайны разделения изотопов 2011

получаются из соотношений (8.5), (8.3) и (8.7) для случая, когда p ′ << p0 , а именно

Для изотопных смесей тяжелых элементов коэффициент обогащения ε0 оказывается заметно меньшим единицы и приближенно записывается в виде

теоретические коэффициенты обогащения при однократном пропускании смеси через пористый фильтр. На самом деле, по ряду причин, о которых мы скажем позже, реальные коэффициенты обогащения на фильтре оказываются меньшими, чем это значение.

В общем случае, когда нужно учитывать величину конечного давления за фильтром , использование уравнений (8.7) и (8.3) при ε0 << 1 дает следующее выражение для скачка концентраций на

Естественно, что при отсутствии перепада давлений на фильтре (k = 1) отсутствует и эффект разделения смеси.

Диффузия в переходной области давлений

Теперь мы попытаемся объяснить, почему с возрастанием давления или увеличением характерного размера пор, (т.е. при переходе в область промежуточных значений числа Кнудсена) происходит заметное уменьшение эффекта разделения по сравнению с его максимальным значением при KN >> 1 . Для этого

181

нам надо понять, как изменяются значения потоков компонентов смеси в капилляре и пористой среде для режима течения, переходного от свободно - молекулярного к вязкому.

Рассмотрим вопрос о выводе уравнений, из которых можно для

здесь потоки, отнесенные к единице площади сечения среды). Для того чтобы учесть одновременно и кнудсеновскую и обычную диффузию газовой смеси в капилляре, воспользуемся опять методом баланса импульса. Обратимся сначала к полученному в предыдущей главе выражению для кнудсеновского потока (7.28)

. В свободно-молекулярном режиме течения потоки каждого из компонентов смеси являются независимыми. В частности, для потока J1K мы имеем

J1K = −(DK )1 dn1 , dx

где D1K = (1 3)d v1 − кнудсеновский коэффициент диффузии для

компонента 1 при течении смеси в капилляре. Такое представление выражения для потока фактически вытекает из уравнения баланса импульса для компонента 1 при учете столкновении его молекул со стенкой капилляра. Соответствующее уравнение с учетом соотношения p1 =n1 kT может быть теперь записано как

Левая часть (8.10) представляет собой силу, действующую на компоненту 1 в единице объема газа, которая обусловлена разностью парциальных давлений этого компонента на бесконечно малой длине dx . Правая часть соответствует средней передаче импульса молекул компонента 1 при их столкновениях со стенкой.

182

бесконечно большие массу и сечения столкновений. Аналогичная модель, названная моделью запыленного газа, была разработана американскими учеными лишь спустя шесть лет [43]. На основе модели стеночного газа Ю. Каганом была создана теория разделения многокомпонентных газовых смесей в пористых средах в переходной области течения [19 ].

Легко усмотреть простую аналогию в записи уравнений баланса импульса (8.12), (8.13) с записью закона Ома для эквивалентной электрической цепи, в которой роль напряжений играют градиенты парциальных плотностей, а роль сил токов − потоки компонентов. Схема такой цепи, объединяющей различные механизмы переноса, представлена на рис. 8.2. При этом следует иметь в виду, что после

вычисления на основании (8.12), (8.13) потоков n1u1 и n2u2 ,

имеющих диффузионную природу, к ним следует добавить составляющую, отвечающую переносу компонента смеси вязким потоком, так что полные потоки компонентов определяются выражениями

где

Здесь K − константа Дарси (для капилляра K = r 2 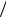8 ).

184

1

Рис.8.2. Эквивалентная электрическая цепь как мнемоническая схема объединения различных механизмов переноса.1 – ветвь диффузионного течения, 2 – ветвь вязкого течения

Решая совместно уравнения (8.12) и (8.13), можно получить не только выражения для самих потоков, но также и выражение для диффузионного потока (J D )1 = nc (1 − c)(u1 − u 2 ) . Последний

результат представляет для нас особый интерес, так как именно с наличием разности скоростей компонентов связан эффект разделения. Получаемое выражение для диффузионного потока можно представить в виде

Здесь D − обобщенный коэффициент диффузии, определяемый соотношением

где (Dk )12 = (Dk )1 (1 − c) + (Dk )2 c .

185

Выражение (8.17) выглядит естественным, если иметь в виду аналогию с эквивалентной электрической цепью (рис.8.2), в которой величины, обратные соответствующим коэффициентам диффузии, выступают в роли электрических сопротивлений.

Коэффициент α p называется постоянной бародиффузии в кнудсеновском потоке и имеет вид

M 1 c + M 2 (1 − c)

Именно наличием бародиффузии в смеси внутри капилляра и определяется эффект разделения. Для изотопных смесей тяжелых элементов выражение для диффузионного потока можно представить в виде

где bp = (DK D11 ) . Для оценки величины bp воспользуемся формулами (7.26) и (7.37) и определением средней длины свободного пробега молекул (7.13). Тогда в случае капилляра имеем

диффузионного потока через капилляр уменьшается примерно в два раза. Напомним, что доля вязкого потока составляет при этом не более 15%.

Заметим теперь, что в соответствии с определениями (7.29) и (8.4) диффузионный поток можно представить в виде

Полный поток J , отнесенный к единице площади сечения капилляра, в случае изотопной смеси определяется как

В результате, используя (8.19) и (8.22), приходим к уравнению,

которое называется уравнением разделения изотопной смеси в капилляре или пористой среде

Это уравнение относится к разряду так называемых дифференциальных уравнений первого порядка, решение которых при граничных условиях, соответствующих в нашем случае входу и выходу из канала, рассматривается в курсах высшей математики. Мы не будем заниматься его решением. Упомянем лишь, что в кнудсеновском режиме течения ( ap → 0, bp → 0 ) его решение приводит к результату, в точности совпадающему с формулой (8.9).

Качественный результат в общем случае можно получить, если в первом приближении пренебречь в (8.23) членом dc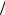 dp , который соответствует обратной диффузии в канале, и заменить с на c0 .

В результате получаем

Из этого выражения следует, что эффект разделения уменьшается главным образом за счет роста величин ap и

bp ~ (r / λ) . К их возрастанию приводит либо повышение давления либо увеличение радиуса канала. При этом увеличение доли вязкого потока сказывается на эффекте разделения менее существенно, чем уменьшение эффективного коэффициента диффузии, поскольку a / b = 0,135. Учет обратной диффузии приводит к еще более сильному падению эффекта. Зависимость

187

скачка концентрации на фильтре можно представить поэтому как функцию от одного из этих параметров, например от bp ~ r / λ и

отношения давлений k= p ′ / p . Реальная зависимость от этих параметров конечно несколько отличается от (8.24), поскольку надо учитывать еще член pdc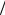 dp в уравнении разделения, который является отрицательным (давление падает, а концентрация растет) и, следовательно, дополнительно уменьшает эффект. Удобно описывать эту зависимость с помощью фактора Z , так что

В кнудсеновском режиме течения смеси через фильтр имеем

Z = 1 .

Вернемся теперь к схеме, изображенной на рис.8.1. Следует сразу подчеркнуть, что хотя сам эффект разделения на фильтре в рассматриваемом нами случае и имеет место, предложенная схема течения газовой смеси через фильтр не может служить прообразом разделяющего устройства (делителя). На самом деле здесь происходит следующее. Поскольку средняя направленная скорость компонентов в пористом фильтре оказывается различной, преимущественный уход одного из компонентов через фильтр приводит к обеднению смеси легким компонентом непосредственно перед его входом. В результате возникает плавное падение концентрации легкого компонента от его исходного значения свх на входе в трубу до значения с0 на входе в фильтр. Это выглядит вполне естественным, поскольку убыль легкого компонента перед фильтром должна пополняться притоком его из области, где поток еще только входит в трубу. Механизмом, поставляющим недостающее количество легкого компонента, является в этом случае обычная диффузия в смеси или перенос компонента в сторону падения его концентрации. Реальное

188

Делитель

Для того чтобы осуществить реальное обогащение смеси легким компонентом, необходимо создать условия, при которых поступающий в делитель поток смеси разделяется на две части, одна из которых содержит обогащенную фракцию, а другая обеднена легким компонентом. На практике делитель представляет собой цилиндрический бак, внутри которого размещены фильтры в виде пучка трубок с пористыми стенками. Принципиальная схема делительного устройства диффузионном методе разделения уже рассматривалась нами в главе 6 (см. рис. 6.1).

Во внутреннее пространство трубок поступает поток питания Q при давлении p и концентрации легкой фракции свх . Этот поток движется вдоль каналов и по мере продвижения часть его

189

проникает через пористые стенки, на внешней стороне которых поддерживается более низкое давление p ′ . Поток обогащенной фракции Q′ (отбор) с концентрацией с′ отводится через общий

выход более низкого давления p ′ < p . Поток газа, не прошедший через фильтры, при течении вдоль каналов постепенно обедняется легким компонентом до концентрации с′′ , уменьшаясь от величины Q на входе до величины Q′′ на выходе при давлении

p ′′ , образуя поток тяжелой фракции (отвал). Потоки и концентрации легкого компонента в различных фракциях удовлетворяют уравнениям сохранения (6.2).

В главе 6 было отмечено, что полное обогащение на газодиффузионной ступени определяется суммой перепадов концентрации, возникающих на трассах обогащенной и обедненной фракций. Соответствующий полный коэффициент обогащения ступени ε должен определяться с учетом непрерывного падения величины потока и концентрации легкого компонента по мере течения потока питания в трубках по трассе обедненной фракции. Если принять, что скачок концентрации на

фильтрами меняется по длине трубок потому же закону, что и перед фильтрами. Рассмотрим, как в этом случае определяется полный эффект обогащения на делителе

Пусть величина потока по трассе обедненной фракции уменьшается на длине dx на величину dQ , так что такая же

величина dQ проходит через фильтры в поток низкого давления (рис.8.3). Если обозначить концентрацию легкого компонента в

рассматриваемом сечении делителя имеет вид

Qc = c′dQ + (Q − dQ ) (c − dc ) .

В пренебрежении малым квадратичным членом dQdc приходим

190