Древс Системы реалного времени технические и программные средства 2010

4. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ

Если измерительную информацию предполагается обрабатывать в системе с помощью цифровой вычислительной машины или с помощью цифрового процессора, то необходимо преобразовать исходный непрерывный (аналоговый) сигнал в дискретный и квантованный (цифровой) сигнал. Для этих целей используются аналого-цифровые преобразователи (АЦП). Выходной сигнал обычно представляется в форме двоичного позиционного кода. Носителями информации во входном сигнале могут быть напряжение, ток, временной интервал, фаза и частота переменного тока. Эти же величины могут служить промежуточными величинами, если по каким-либо причинам прямое преобразование входной величины в код нецелесообразно.

Аналого-цифровые преобразователи классифицируют по виду информативного параметра на его входе и выходе.

4.1. Преобразователи напряжения в частоту

Эти преобразователи относятся к аналого-цифровым преобразователям, поскольку в них изменяющийся во времени аналоговый сигнал – напряжение преобразуется в последовательность импульсов, частота которых прямо пропорциональна текущему его значению. Число этих импульсов за фиксированный промежуток времени представляет собой число-импульсный код, который при необходимости может быть преобразован в двоичный или десятичный. В ряде случаев такие преобразователи обладают определенными преимуществами перед АЦП других типов.

Преобразователи напряжения в частоту могут быть прямого и импульсно-компенсационного типа.

Преобразователи прямого преобразования. Преобразователя такого типа работают по следующему принципу. Входное напряжение uвх(t) поступает на вход интегратора. Его выходное напряжение с помощью схемы сравнения сравнивается с некоторым за-

101

данным напряжением u0. Сигнал равенства этих напряжений возвращает интегратор в исходное состояние, что обеспечивает развертку процесса во времени.

Общее условие, из которого можно найти выходную частоту, имеет следующий вид:

где T – период следования выходных импульсов. Поскольку входное напряжение поступает с выхода схемы выборки–хранения, оно может считаться постоянным в течение времени преобразования.

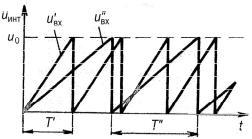
Временные диаграммы выходного напряжения интегратора для разных постоянных входных напряжений ивх и ивх показаны на

рис. 4.1. Выходная частота, т.е. частота следования сигналов совпадения на выходе схемы сравнения, пропорциональна среднему значению входного сигнала.

Рис. 4.1

На практике мгновенный возврат интегратора в исходное состояние неосуществим. Поэтому применяют изменение направления интегрирования, формируя обратный ход «пилы» за определенное время. Если параметры интегрирования в прямом и обратном направлении одинаковы, то выходная частота будет в два раза меньше по сравнению с идеальным случаем мгновенного сброса.

Изменение направления интегрирования производится одним из следующих способов [4]:

1)подачей параллельно входному напряжению интегратора выходного сигнала инвертирующего масштабного усилителя;

2)коммутацией полярности входного напряжения интегратора;

102

3) изменением знака разности напряжений между инвертирующим и неинвертирующим входами ОУ интегратора.

При подаче на вход переменного входного сигнала пилообразные выходные напряжения интегратора становятся нелинейными и текущая частота изменяется от периода к периоду. Рассмотрим для примера прямое преобразование линейно нарастающего сигнала

uвх(t) = uвх + (duвх / dt)t.

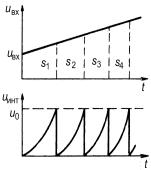
Интеграл напряжения представляет собой сумму двух функций – линейной и квадратичной. Временные диаграммы показаны на рис. 4.2. При анализе следу-

Импульсно-компенсационные преобразователи. Если вход-

ное напряжение изменяется во времени, а компенсирующее напряжение uк (t) имеет форму прямоугольных импульсов длительности tк, то компенсация за период следования импульсов Т осуществляется средним значением импульсного напряжения:

Очевидно, что амплитуда компенсирующих импульсов должна быть больше среднего значения входного напряжения, а их полярность – противоположной.

Преобразователь (рис. 4.3, а) включает в себя суммирующий интегратор, нуль-индикатор НИ, сигнализирующий об окончании компенсации, оговоренной условием (4.2), и генератор стабильных одиночных импульсов ГСОИ, запускаемый выходным сигналом НИ. Временная диаграмма работы преобразователя показана на рис. 4.3, б. В результате возрастания выходного напряжения интегратора под действием входного сигнала срабатывает НИ и запус-

103

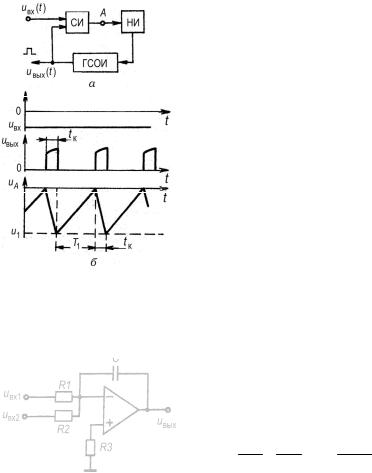
кает ГСОИ, который генерирует импульс длительности tк. В течение этого импульса напряжение снижается до значения и1. После окончания компенсирующего импульса напряжение на выходе интегратора опять возрастает. Когда оно достигнет нулевого значения, опять сработают НИ и ГСОИ, и начнется новый цикл работы преобразователя.

Максимальная рабочая частота преобразователя «напряжение–часто- та» достигает 1 МГц, нелинейность не превышает 0,01 %.

Рассмотрим подробнее принципы построения основных функциональ-

ных блоков преобразователей напряжения в частоту. Суммирующий интегратор. Интегратор такого типа интегри-

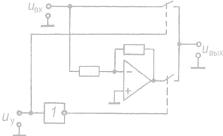
рует алгебраическую сумму нескольких подаваемых на разные вхо- ды напряжений. Схема суммирующего интегратора для двух напряжений показана на рис. 4.4. Работа этой схемы описывается дифференциаль-

ным уравнением

uвх1 uвх2 C duвых .

В результате решения этого уравнения относительно uвых получим:

Возврат интеграторов в исходное положение может производиться быстрым разрядом конденсатора или подключением через

104

резистор к одному из входов ОУ такого напряжения, при котором изменяется направление интегрирования.

Источники опорного напряжения. Простейшая схема такого источника может быть выполнена на прецизионном кремниевом стабилитроне. Однако на стабильность напряжения в такой схеме влияют изменения сопротивления нагрузки и тока через стабилитрон. Для улучшения характеристик стабилитрон подключают к неинвертирующемувходуОУ и питают егоот стабилизатора тока.

Коммутаторы полярности напряжения. Для коммутации по-

лярности напряжения применяются схемы с транзисторным ключом в цепи его неинвертирующего входа или интегральные ключи на КМОПструктурах. На рис.4.5 показана схема переключения полярности. Она содержит двухканальный интегральный ключ, инвертирующий усилитель на ОУ с единичным усилением и инвертор.

Когда управляющее напряжение иу представляет собой логическую единицу, входной сигнал ивх проходит на выход через замкнутый верхний ключ схемы, при этом нижний ключ разомкнут. Когда на управляющий вход поступает логический нуль, верхний ключ разомкнут, нижний – замкнут и выходной сигнал имеет полярность, противоположную полярности входногосигнала.

4.2. Преобразователи временного интервала, фазы и частоты в код

Эти преобразователи применяются как в качестве самостоятельных схем, так и в составе других типов АЦП, использующих двойное преобразование. В ряде случаев такой вариант построения оказывается предпочтительным.

Преобразователи временного интервала в код. В этих преоб-

разователях используется метод последовательного счета. Времен-

105

ной интервал заполняется импульсами тактового генератора стабильной частоты, и его величина характеризуется количеством импульсов, которые укладываются в этом интервале. Схема такого преобразователя приведена на рис. 4.6. Началу временного интервала соответствует старт-импульс. Он устанавливает триггер Т в 1, благодаря чему импульсы от генератора ГИ с частотой f = 1/t начинают поступать на счетчик через схему И. Концу временного интервала соответствует стоп-импульс, который переводит триггер в 0, после чего поступление импульсов на вход счетчика прекращается. Следовательно, код счетчика представляет собой длину временного интервала T = (n 1)t, где n – число импульсов, поступивших на счетчик.

Рис. 4.6

Поскольку старт- и стоп-импульсы несинхронны по отношению к тактовым импульсам, могут возникнуть погрешности: t1 – задержка первого тактового импульса относительно стартового и t2

– задержка стоп-импульса относительно последнего тактового. Поэтому истинное значение временного интервала

T* = (n 1)t + t1 + t2.

Если первую составляющую погрешности можно устранить, применяя специальные схемотехнические приемы, то вторая составляющая принципиально неустранима; ее можно только сократить.

Преобразование фазы в код. Обычно в качестве преобразуемой величины используется разность фаз опорного сигнала f0(t) и

106

входного сигнала fвх(t), информативным параметром которого является фаза. Как правило, имеют дело с синусоидальными сигналами одинаковой частоты.

Наиболее распространенный метод – переход от сдвига фаз к временному интервалу с последующим преобразованием его в код. Для этого фиксируются моменты перехода через нулевой уровень опорного и входного сигналов; соответствующие импульсы служат старт- и стоп-импульсами (см. выше).

Периоду Т опорного и входного сигналов (он задан) соответствует сдвиг фаз, равный 2 ; сдвигу фаз – длительность временного интервала Ти (он измеряется). Составляя пропорцию, имеем: Tи =T/2 . Переходя далее к кодам и полагая, что длительности Т соответствует число импульсов N, а длительности Ти – n, имеем: = 2 n/N.

На точности преобразования сказывается наличие высокочастотных помех во входном сигнале. Их влияние уменьшается путем выбора для фиксации сдвига фаз нулевого уровня: здесь крутизна синусоиды максимальна и аддитивная высокочастотная помеха меньше искажает результат сравнения.

Точность можно также повысить, применяя статистическую обработку результатов нескольких измерений (если только изменениями измеряемой фазы за это время можно пренебречь). В простейшем случае это обеспечивается вычислением сдвига фаз во время прохода обоих сигналов через нулевой уровень дважды: в прямом и в обратном направлениях.

Модификация рассмотренного метода: синусоидальные сигналы заменяются прямоугольными импульсами соответствующей полярности. С помощью элемента И легко выделить последовательность разнополярных импульсов, длительность которых Ти, пропорциональная измеряемому сдвигу фаз, может быть измерена рассмотренным выше преобразователем.

Количество импульсов ГИ, поступивших с частотой f = 1/tги за один период преобразования, равно Ти/tги. Если выбрать интервал усреднения Tус = kТ, а частоту f так, чтобы T = k1tги (k и k1 – посто-

107

янные, выбранные из условия неизменности сдвига фаз или по требуемой точности, если анализу подлежит средняя частота), то общее количество импульсов, поступивших за время Тус,

N = (Тус/Т)(Ти/ tги) = kTи/tги = k T/2 tги = kk1/2 .

Видно, что результат измерений инвариантен относительно изменения частоты ГИ и частоты синусоидальных сигналов, т.е. этот метод позволяет исключить два источника погрешностей.

Преобразователи фазы в код часто являются составной частью измерителей перемещений, в которых перемещение сначала преобразуется в фазовый сдвиг, а затем – в код.

Преобразователи частоты в код. Для преобразования частоты в код можно в качестве измеряемой величины использовать: 1) период измеряемой частоты; 2) количество периодов за фиксированный промежуток времени; 3) приращение фазы за фиксированный временной интервал.

Первый случай соответствует задаче преобразования временного интервала в код (см. выше), однако следует учитывать, что вычисление частоты по измеренному периоду требует наличия функциональных (гиперболических) преобразователей или процессора.

Реализация второго способа связана с подсчетом периодов (если входной сигнал гармонический, то предварительно его рекомендуется преобразовать в последовательность импульсов) и заданием фиксированного временного интервала. Его длительность должна выбираться с учетом требуемой точности измерения и может изменяться при изменении измеряемой частоты. Для измерения высоких частот используется принцип гетеродинирования.

Третий способ основан на том, что частоту можно определить как отношение приращения фазы к отрезку времени, за который произошло это приращение. Таким образом, проведя два преобразования фазы в код на известном и фиксированном временном интервале, можно определить значение частоты. Обязательным условием, обеспечивающим точность измерения, является строго фиксированная и неизменная форма входного сигнала (предпочтительно – синусоида).

108

4.3. Преобразователи напряжения в код, построенные по принципу последовательного счета

Способы преобразования напряжения в код. Процесс преобра-

зования напряжения в код можно реализовать разными способами. На практикенаибольшеераспространениеполучили три метода:

-метод последовательного счета, при котором входная анало-

говая величина уравновешивается последовательно накапливаемой суммой одинаковых минимальных эталонов, называемых квантами. Момент равенства входной величины и суммы эталонов определяется с помощью одного сравнивающего устройства. Результат преобразования характеризуется числом квантов, накопленных при формировании суммы;

-метод поразрядного кодирования, при котором входная вели-

чина последовательно сравнивается с суммой эталонов, накопленных за предыдущие циклы сравнения. «Вес» каждого эталона равен

iквантам, где i последовательно принимает значения n 1, n 2, ..., 2, 1, 0 (n – число разрядов АЦП). Если результат сравнения на i-м шаге положителен (входная величина больше накопленной суммы), то соответствующий эталон прибавляется к сумме, и в i-м разряде выходного регистра устанавливается 1. В противном случае эталон не добавляется, разряд устанавливается в 0 и следует переход к следующему, более «легкому» эталону. Сравнение входной величины и суммы эталонов выполняется последовательно одним сравнивающим устройством, результат преобразования характеризуется совокупностью единиц и нулей в выходном регистре;

-метод параллельного сравнения, при котором входная вели-

чина одновременно сравнивается с полной совокупностью этало-

нов, равных 1, 2, 4, 8, ..., n 1 квантам. Результат преобразования характеризуется количеством компараторов, отметивших равенство или превышение входной величины по отношению к данному эталону, и представляется последовательностью единиц и нулей. Для получения выходного позиционного кода требуется соответствующее преобразование этого промежуточного результата.

109

Как видно, каждый метод требует разных аппаратурных затрат (числа эталонов и компараторов) и обеспечивает разное время преобразования. В зависимости от системных требований выбирается тот или иной метод.

Преобразователь последовательного счета (с обратной свя-

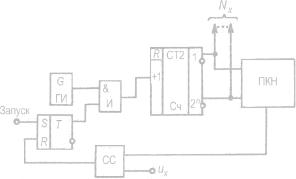
зью). Для реализации принципа последовательного счета, который был кратко описан выше, требуется один эталон, равный кванту. Он многократно используется для уравновешивания входной аналоговой величины. Именно в таком виде этот принцип реализован в преобразователе «напряжение – код» (ПНК), структурная схема которого показана на рис. 4.7.

Рис. 4.7

Импульс запуска через элемент И поступает на счетчик. Обратная связь реализована с помощью преобразователя код– напряжение (ПКН): выходы счетчика соединены с входами ПКН и при поступлении на счетчик очередного импульса вместе с увеличением на единицу его содержимого возрастает на одну «ступеньку» напряжение на выходе ПКН. Величина приращения напряжения за один такт равна кванту. Компаратор (схема сравнения СС) закроет элемент И, когда выходное напряжение ПКН достигнет уровня входного сигнала ux. Состояние счетчика в этот момент является цифровым выходным сигналом ЦАП.

Основной недостаток этого простого способа – зависимость времени преобразования от уровня входного сигнала, причем это

110