2. Базисное решение задачи лп.

Рассмотрим стандартную задачу вида

при ограничениях

()

().

Задача содержит nпеременных иmограничений, представленных в виде неравенств.

Переходя к канонической задаче получаем:

(1)

при ограничениях

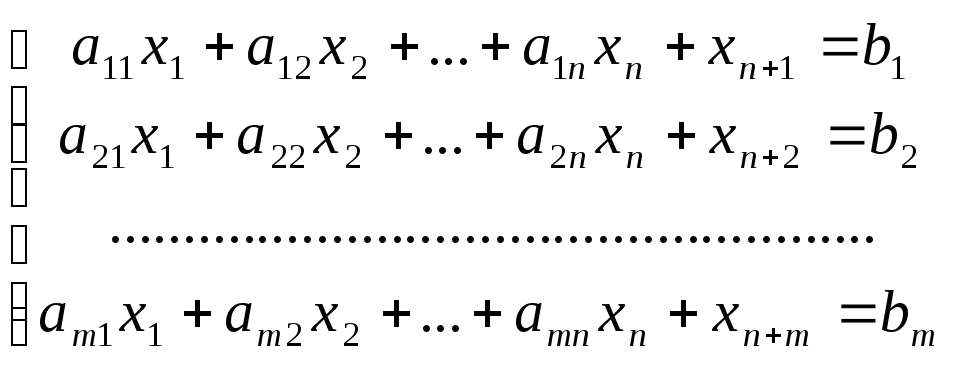(2)

(); (3)

() – слабая переменная. (4)

Система (2) имеет бесчисленное множество решений, т. к. содержит mуравненийn+mнеизвестных.

Чтобы получить некоторое решение системы (2) приравниваем нулю nнеизвестных. Полученная система изmуравнений сmнеизвестными будет иметь решение, еслиопределитель этой системы отличен от нуля. В противном случае можно выбрать другиеnнеизвестных и приравнять их к нулю.

Таким образом, базисом называют любой набор изmпеременных, для которых определитель, составленный из коэффициентов при этих переменных, не равен нулю.

Полученное при этом решение называют базисным, а переменные, которые были приравнены к нулю называютсясвободными.

Эти mпеременных называютбазисными. Остальныеnпеременных называют свободными. (Свободные переменные = 0)

Т. о., если приравнять все свободные переменные нулю, то можно решить полученную систему из mуравнений сmнеизвестными. Полученное при этом решение называютбазисным.

Замечание: Для каждой конкретной системы (2) может существовать несколько различных базисов с различными базисными переменными и базисными решениями.

Среди возможных базисных решений могут быть такие, которые дают отрицательные значения некоторых переменных. Это противоречит постановке задачи (3), (4), а решение является недопустимым.

Допустимым базисным решением (дбр) является такое базисное решение, для которого все базисные переменные принимают неотрицательные значения.

Число допустимых базисных решений конечно и все они удовлетворяют ограничениям исходной задачи. Среди этих решений находится оптимальное (max), которое необходимо найти в процессе решения задачи ЛП.

3. Геометрическая интерпретация задачи лп.

Позволяет проиллюстрировать понятие допустимого базисного решения и показать, что именно среди этих решений находится оптимальное.

Рассмотрим пример. Найти

при ограничениях

Перепишем в виде

В данном примере число уравнений m= 3, а число неизвестныхm+n= 5, т. е. число свободных переменныхn= 2. Это дает возможность решить задачу графически в двумерном пространстве, т. е. на плоскости.

Систему трех уравнений можно решить относительно трех переменных, выразив их через остальные переменные.

В частности:

Каждое из уравнений ,определяет некоторую полуплоскость, задаваемую в координатахи.

Например, определяет правую полуплоскость относительно оси,- верхнюю полуплоскость относительно оси.

Области и считаются запрещенными и отмечаются штриховкой.

Условие определяет некоторую полуплоскость, лежащую по одну сторону от прямой, а именно ту, которая содержит начало координат.

В этом легко убедиться, если подставить координаты точки (0, 0) в уравнение и проверить значение .

Для всех ограничений одновременно получаем

6

4

1

Допустимой областью значений и является выделенный многоугольник.

Чтобы получить максимум целевой функции рассмотрим уравнение, которое определяет прямую при любом фиксированномz.

Например, для z= 2 имеем(см рисунок). Увеличиваяzбудем получать семейство параллельных прямых. Решение оптимизационной задачи будет в той точке, гдеzмаксимально, а полученная прямая имеет хотя бы одну общую точку с допустимой областью решений.

Для обобщения результатов рассмотрим постановку задачи в виде:

(1)

семейство гиперплоскостей при ограничениях

() (2)

Уравнение (3) определяет неотрицательную область в пространстве :

(); (3)

Полупространство, ограниченное одной из гиперплоскостей (2)

(); (4)

где имеется mуравнений в ограничениях приm+nнеизвестных.

Каждое из неравенств (3) определяет в n– мерном евклидовом пространстве некоторое замкнутое полупространство. Пересечение всех этих полупространств дает неотрицательный октант (квадрант приn= 2) вn– мерном пространстве.

Пересечение всех замкнутых полупространствдает выпуклый многогранник, расположенный в неотрицательном октантеn– мерного пространства.

Примеры таких многогранников:

Х

n=2;m=3

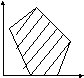
Х

n=2;m=4

n=3;m=4

Поверхности равных значений zцелевой функции представляют собой семейство параллельных гиперплоскостей (плоскостей приn= 3; прямых приn= 2). Поэтомуэкстремум целевой функции в задаче ЛП достигается в одной или нескольких вершинах многогранника решений.

Замечание: Каждая вершина многогранника допустимых решений в задаче ЛП соответствует одному из допустимых базисных решений, т. к. все вершины лежат в неотрицательном октанте (все переменные неотрицательны) и для любой из нихне менее n переменных равны нулю (число переменных, равных нулю, совпадает с числом пересекающихся граней).

Для поиска оптимального решения можно просмотреть все допустимые базисные решения или вершины многогранника, число которых конечно.

Однако в реальных задачах их число может быть очень большое, поэтому применяются специальные методы направленного перебора, обеспечивающие сокращение числа просматриваемых допустимых базисных решений.