Гаврилов Оборудование для работы с ускоренными пучками 2010

Наибольшее подавление фона происходит, если выбираются события, состоящие из комбинации: l + νl + N jets (l = e, μ), где N ≥ 3 и лептон, и струи (jets) имеют большой поперечный импульс (более 20 ГэВ/c). Идентификация W аналогична, применяемой в эксперименте UA1.

В 1994 г. на установке CDF наблюдали 12 кандидатов при фоне шесть событий. Вероятность того, что эти 12 событий есть флуктуация фона – 0,26 %.

Для чего строят новые коллайдеры? Взаимодействия между кварками, лептонами и калибровочными бозонами детально исследованы на существующих коллайдерах. Результаты экспериментов согласуются с потрясающей точностью с предсказаниями Стандартной Модели. Казалось незачем строить новые коллайдеры. Но цена этого согласия введение в теорию «руками», по крайней мере, 18 произвольных параметров, которые мы получаем из эксперимента.

На адронном коллайдере обычно наблюдают новые явления (частицы). Детальное исследование этих явлений проводят на элек- трон-позитронном коллайдере.

При высоких энергиях адронный коллайдер, по существу, превращается в кварковый коллайдер. Взаимодействие кварков происходит в диапазоне импульсов, определяемом распределением кварков по импульсу в адроне. В отличие от адронного коллайдера, на е+ е--коллайдере можно точно выбрать энергию взаимодействия, например, соответствующую массе исследуемой частицы.

Калибровочные бозоны W и Z впервые обнаружены на адроном коллайдере, SppS , а затем детально исследованы на е+е-- кол-

лайдере LEP. Аналогичная история произошла и с частицами, содержащими c и b кварки.

Основным назначением LHC и задачей № 1 всей физики высоких энергий является поиск бозона Хиггса – частицы ответственной за появление массы у W- и Z-бозонов и фермионов. После LHC построят большой электронный и возможно даже мюонный коллайдер.

Ожидают, что на LHC будем наблюдать новые яркие явления в физике элементарных частиц, разобраться в природе которых помогут электрон-позитронные и мюонные коллайдеры.

32

2. НЕКОТОРЫЕ СВОЙСТВА МАТРИЧНОГО ПРЕДСТАВЛЕНИЯ

Рассмотрение динамики заряженных частиц в магнитных системах в линейном приближении будет проведено с помощью матричного представления, которое было использовано при анализе устойчивости движения частиц в ускорителях. Его формализм оказался очень удобным при изучении движения в различных элементах магнитных систем электрофизического оборудования, когда скорости частиц близки к скорости света.

2.1. Свойство элементов матриц

Сначала рассмотрим моноимпульсные пучки частиц, т.е. такие пучки, для которых разброс по импульсам отсутствует, а именно: ∆р/р0 = 0, где р0 – номинальный импульс, а ∆р – разброс по импульсу. В этом случае для описания магнитной системы может быть использована квадратная матрица второго порядка

В ортогональной плоскости будут использована другая матри-

матрицу 4-го порядка.

Для системы, состоящей из нескольких элементов, каждый из которых характеризуется своей матрицей, общая матрица представляет произведение отдельных матриц:

33

где Ti – матрица i -го элемента.

Необходимо помнить, что из-за не коммутативности в произведении матриц должна быть соблюдена строгая последовательность:

квходному вектору x0 примыкает матрица входного элемента, а

x0′

квыходному – конечного:

Отметим значение отдельных элементов матрицы T. Элемент T21 равен оптической силе системы, взятой с обратным знаком, т.е.

плоскости. Для того чтобы показать это, рассмотрим траекторию частицы, параллельную оси x0 ≠ 0 , x0′ = 0 . Месторасположение

главной (выходной) плоскости, перпендикулярной оси системы, проходит через точку пересечения продолженных внутрь системы входной и выходной траекторий. Главную плоскость системы траектория пересечет при x = x0 , а на выходе ее будем иметь угол на-

клона, отличный от нуля:

где S – расстояние, которое отсчитывается от главной выходной плоскости.

Траектория показана на рис. 2.1. Естественно, что реальная траектория будет плавной, а не ломаной, состоящей из отрезков прямых линий. Подставляя значение x1′ из выражения (2.5) в урав-

34

мость следует из уравнений (2.10), а достаточность – из того, что, если х1 = 0 при х0 = 0, то Т11 = 0.

Если же траектория наклонена к оси x0′ ≠ 0 , то она будет пересекать ось под углом, определяемым (2.5).

Вслучае Т12 = 0 точечный источник 0 преобразуется в точ-

x0′

ку:

x1 =T11 x0 + x0′T12 = 0 .

Если же источник имеет конечные размеры, т.е. x0 ≠ 0 , то при

Таким образом, в матрице преобразования Т при Т12 = 0 элемент Т11 есть коэффициент линейного увеличения. Обозначим его через М. При том же условии Т12 = 0, а также при х0 = 0 и x0′ ≠ 0 наклон траектории после прохождения системы равен x1′ =T22 x0′ .

Следовательно, элемент Т22 есть коэффициент углового увеличения.

Из теоремы Лиувилля следует, что определитель матрицы консервативной системы равен единице, поэтому

Форма матрицы (2.13) похожа на форму матрицы тонкой линзы (в матрицах тонких линз элементы по диагонали Т11 и Т22 равны 1). Назовем эту диагональ главной. Следовательно, равенство Т12 = 0 означает, что расположенный до системы источник заряженных частиц будет иметь изображение после прохождения последними системы.

36

В случае T22 = 0 (угловая коллимация) точечный расходящийся

0

пучок переходит в параллельный. Действительно, из уравне-

x0′

ния (2.2) следует, что

заданной выходной апертуре х1 пропускаются частицы, имеющие наклон не более чем x0′ на входе в систему.

в параллельный. Действительно, из выражения (2.2) найдем, что

x1 =T11 x0 , x1′ = 0 ,

и на выходе системы имеем параллельную оси системы траекторию

свектором T11x0 . Система с матрицей, в которой элемент Т21 = 0,

0

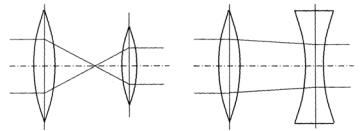
называется телескопической. Аналогом телескопической системы в геометрической оптике служат комбинации линз, которые преобразуют параллельный пучок в параллельный с новыми поперечными размерами. Если элемент T11 < 0 , то на выходе изображения бу-

дет перевернуто (рис. 2.2, а), а если T11 > 0 , то оно будет сохранять первоначальное направление (рис. 2.2, б).

а б

Рис. 2.2. Телескопические системы:

T11 < 0 (а) и Т11 > 0 (б)

37

Равенство нулю матричного элемента означает, что одна из составляющих вектора на выходе не зависит от какой-либо входной составляющей того же вектора.

Из-за того, что определитель матрицы (2.1) равен единице, элемент, диагонально расположенный к нулевому, может иметь произвольную величину. При этом произведение двух остальных элементов должно быть равно единице.

2.2. Равенство единице определителя матриц

Покажем, что все матрицы, которые будут использоваться в дальнейшем, имеют определитель, равный 1. Проведем рассмотрение для матриц второго порядка, однако все полученные выводы будут справедливы и для матриц более высокого порядка. Это будет видно непосредственно из матриц.

Согласно теореме Лиувилля плотность точек фазового пространства является инвариантом движения для системы, описываемой уравнениями Гамильтона

где Н – гамильтониан, а qi и pi – канонические координаты. Кроме того, можно отметить, что фазовый объем, в котором заключены эти точки (им соответствуют траектории частиц), может меняться по форме при сохранении величины в течение всего движения, а именно:

где d dq1,...,dqn ,dp1,...,dpn – элемент фазового объема. В данном

случае фазовый объем ведет себя как несжимаемая жидкость. Если переменные в уравнениях движения разделяются или горизонтальное и вертикальное движения независимы, то теорема Лиувилля оказывается справедливой для каждой пары координат и импульса. Следовательно, движение можно рассматривать на плоскости.

Перейдем непосредственно к доказательству равенства определителя единице. Для доказательства следует обратиться к рис. 2.3.

38

где хi и xi′ – координаты точек на фазовой плоскости, которые при-

менительно к рис. 2.3 равны х1 = а1, х2 = b2, х3 = 0, x1′ = a1′, x2′ = b2′, x3′ = 0 . Следовательно,

Следовательно, определитель матрицы системы, в которой работает теорема Лиувилля, равен единице. Хотя доказательство проводилось для треугольников, его нетрудно распространить на любую фигуру.

Доказательство равенства (2.25) можно было бы провести, используя вронскиан системы, однако данная методика представляется более наглядной. Следует отметить, что если система составлена из элементов, каждой из которых имеет матрицу с определителем, равным единице, то общая матрица этой системы также будет иметь единичный определитель. Это свойство удобно использовать для проверки правильности перемножения матриц.

40