
Архангелский ПСпице и Десигн Центер Ч1 1996
.pdf
5.6. Формальные макроромодели аналоговы устройств |
181 |
времени τ, соответствующую промежуточному каскаду макромодели, можно определить из соотношения:
τ = |
1 |
|
. |
|
|
2 |
|||
ωн |
|
|
− 1 |
|
[1 + (ωн τ1 )−2 ] |
[1 + (ωн τ2 )−2 |
] |
||
Если входная и выходная цепи вносят только один дополнительный полюс с постоянной времени τ1, то в этом выражении следует положить τ2=∞. Если дополнительных полюсов вообще нет, то обе постоянные времени бесконечно большие и выражение переходит в приведенное ранее: τ=1/ωн.
При наличии дополнительных полюсов, вообще говоря, может возникнуть ситуация, когда определенные по приведенным соотношениям постоянные времени τ оказываются мнимыми величинами. Это означает, что для моделируемого устройства невозможно построить макромодель рассматриваемой структуры, которая одновременно отражает без ошибок частотные зависимости коэффициента передачи, входного и выходного импедансов. Тогда приходится или усложнять макромодель, или жертвовать точностью одной из характеристик. Обычно целесообразно пожертвовать точностью описания входных и выходных импедансов, поскольку все-таки коэффициент передачи - основная характеристика устройства.
Моделирование высших и низших частот отдельными каскадами макромодели целесообразно для широкополосных усилителей, для которых частотные характеристики заданы граничными частотами. При моделировании избирательных усилителей, заданных резонансной частотой и добротностью эти два каскада макромодели объединяются в один, т.е. в макромодель включается параллельный LC контур, зашунтированный сопротивлением R. Расчет параметров макромодели в этом случае ведется по известным формулам, описывающим характеристики контура.
Следует отметить, что, кроме рассмотренных каскадов макромодели, имитирующих частотные зависимости коэффициента передачи, есть еще один путь отображения в макромодели частотных характеристик - применение зависимых источников напряжения или тока с опциями
LAPLACE или FREQ (см. п. 2.3.9). Пользуясь опцией LAPLACE, можно описать в операторной форме частотную зависимость с любым требуемым числом полюсов. Впрочем, это требует сложной подгонки параметров операторного выражения. А пользуясь опцией FREQ, можно в табличном виде отразить по точкам зависимость от частоты амплитуды и фазы коэффициента передачи, причем с любой требуемой точностью. Если
182 |
5. Макромоделирование |
исходными данными для построения макромодели являются АЧХ и ФЧХ, полученные экспериментально или как результат моделирования устройства на уровне компонентов, то использование опции FREQ позволяет построить практически идеальную макромодель со сколь угодно высокой точностью описания частотных характеристик. К сожалению, такую макромодель можно без проблем использовать в дальнейшем только для проведения расчета по постоянному току и малосигнального анализа. А использование такой макромодели для расчета переходных процессов вызывает существенные сложности, описанные в п. 2.3.9.
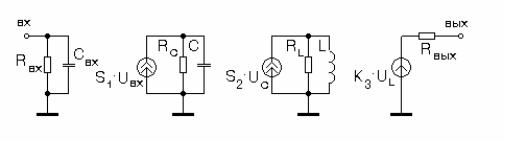
В заключение рассмотрим пример макромодели линейного усилителя напряжения, с заданными значениями входного и выходного сопротивлений Rвх и Rвых, входной емкостью Cвх, заданным коэффициентом усиления К и заданными граничными частотами fв и fн. Возможный вариант такой макромодели приведен на рис. 5.19. Первый ее каскад отражает входное сопротивление Rвх и входную емкость Cвх. Второй каскад отражает верхнюю граничную частоту fв. Сигнал на вход второго каскада передается зависимым источником тока с крутизной S1, управляемым входным сигналом. Напряжение на емкости UС передается зависимым источником тока с крутизной S2 на вход третьего каскада, отражающего нижнюю граничную частоту fн. А напряжение на индуктивности UL передается зависимым источником напряжения с коэффициентом передачи К3 на выходной каскад, моделирующий выходное сопротивление Rвых. Развязка каскадов зависимыми источниками тока и напряжения позволяет легко рассчитывать параметры макромодели независимо друг от друга. Конечно, в любой части макромодели источник тока можно заменить источником напряжения и наоборот.
Рис. 5.19. Макромодель усилителя
Рассмотрим на данном примере расчет параметров макромодели. Выходное напряжение в области средних частот при нулевом сопротивлении источника сигнала и бесконечном сопротивлении нагрузки (как уже было сказано, именно в этих условиях рассчитываются параметры для усилителя
5.6. Формальные макроромодели аналоговы устройств |
183 |
напряжения) равно Uвых=Uвх S1 RС S2 RL К3. Значит, коэффициент усиления в области средних частот К=S1 RС S2 RL К3. Это соотношение представляет собой уравнение с пятью неизвестными параметрами: S1, S2, К3, RС, RL. Следовательно, четыре из них можно выбрать произвольно (включая RС и RL, поскольку граничные частоты можно обеспечить выбором C и L), а пятый рассчитать из заданного коэффициента усиления. Например, можно задать S1=S2=1, RС=RL=1, и тогда коэффициент К3 должна быть равен коэффициенту усиления К.
Величина емкости C определяется из верхней граничной частоты: С RС=1/2πfв, поскольку расчет ведется на нулевое сопротивление генератора и входная емкость Cвх в этих условиях не влияет на коэффициент усиления. Если бы в задании была указана еще и выходная емкость Cвых, то выражение для расчета C изменилось бы, как указывалось ранее, и надо было бы еще учесть постоянную времени τ1=Cвых Rвых. Индуктивность L определяется из нижней граничной частоты: L=RL/2πfн. Если бы на входе и на выходе были разделительные конденсаторы, то это выражение надо было бы изменить, как указывалось ранее для учета соответствующих постоянных времени входной и выходной цепей.
Если бы был задан усилитель тока, а не усилитель напряжения, то макромодель была бы той же самой, но изменился бы расчет коэффициента усиления. Выходной ток при коротком замыкании на выходе равен
Iвых=Iвх Rвх S1 Rc S2 RL К3/Rвых, а коэффициент усиления по току
КI=Rвх S1 Rc S2 RL К3/Rвых. Опять имеется одно уравнение с пятью неизвестными параметрами, четыре из которых можно выбрать произвольно.
5.6.4. НЕЛИНЕЙНЫЕ ИСКАЖЕНИЯ
184 |
5. Макромоделирование |
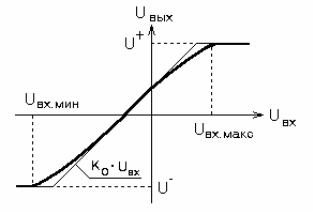
Если макромодель предназначена для использования в режиме большого сигнала, то в ней надо учитывать нелинейные искажения, ограничивающие динамический диапазон реального усилителя. В общем случае передаточная характеристика усилителя в области средних частот имеет вид, представленный на рис.
5.20. На нем диапазон входных
Рис. 5.20. Нелинейная передаточная характеристика
сигналов от Uвх.мин до Uвх.макс, соответствующий примерно
линейному участку характеристики, является динамическим диапазоном. Если макромодель строится на основании справочных данных, то обычно детали нелинейной передаточной характеристики
неизвестны. Заданы бывают только Uвх.мин и Uвх.макс или соответствующие им предельные выходные напряжения U- и U+. В этих случаях передаточную характеристику можно аппроксимировать тремя отрезками прямых, как показано на рисунке тонкими линиями, задавая внутри динамического диапазона наклон, соответствующий коэффициенту усиления К0, а вне динамического диапазона - нулевой или произвольный малый наклон.
Перегрузки, приводящие к нелинейным искажениям, могут быть двух видов:
-перегрузки входных или промежуточных каскадов усилителя;
-перегрузки выходных каскадов.
Перегрузки первого вида физически зависят от входного сигнала, а второго - от выходного. В области средних частот выходной сигнал однозначно связан с входным: Uвых=К0 Uвх, где К0 - коэффициент усиления в области средних частот. Поэтому в области средних частот эти перегрузки неразличимы. Соответственно в макромодели достаточно было бы просто отразить передаточную характеристику. Однако на переходных процессах, когда коэффициент усиления становится комплексной величиной и выходной сигнал теряет однозначную связь с мгновенными значениями входного сигнала, различные виды перегрузок сказываются по-разному.

5.6. Формальные макроромодели аналоговы устройств |
185 |
Перегрузки на выходе не проявляются, пока Uвых не достигает одного из своих предельных значений: максимального U+ или минимального U-. Если считать, что внутри динамического
диапазона |
коэффициент |
|
усиления |
||
постоянный |
и |
равен |
К0, |
то |
в |
пределах U-/К0≤Uвх≤U+/К0 перегрузок на выходе нет. Тогда, как в любой линейной
цепи, длительность фронта выходного сигнала при подаче на вход ступеньки не зависит от амплитуды входного сигнала и равна tф=2,2τв, где τв=1/ωв. Если же амплитуда Uвх превысит, например, величину U+/К0, то время фронта начинает зависеть от амплитуды сигнала, так как часть переходного процесса
“срезается” (рис. 5.21), он не успевает закончится и с ростом амплитуды входного сигнала фронт на выходе уменьшается. Если бы действовал только этот механизм, то с ростом амплитуды входного сигнала фронт на выходе стремился бы к нулю.
Перегрузки во входных и промежуточных каскадах проявляются иначе. Если, например, транзистор во входном каскаде усилителя закрылся или вошел в насыщение, то амплитуда сигнала, поступающего на последующие каскады усилителя, становится постоянной и перестает зависеть от дальнейшего увеличения входного сигнала. Соответственно и фронт на выходе перестает зависеть от амплитуды входного сигнала. Тем самым прекращается уменьшение фронта с ростом амплитуды, вызванное перегрузками на выходе. Этим объясняется ограничение скорости нарастания выходного сигнала усилителя и определяется существенный параметр многих усилителей - максимальная скорость отклика Sот=макс( Uвых/ t) при большом входном сигнале.
Иными словами, различие между перегрузками на входе и выходе заключается в том, что в первом случае фронт формируется после ограничения сигнала, а во втором случае - до ограничения. С этим и связано различное влияние этих перегрузок на фронты сигналов.
186 |
5. Макромоделирование |
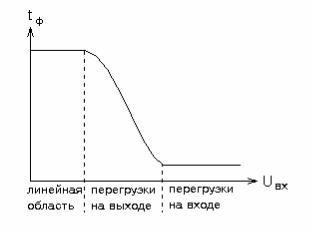
Часто перегрузки на выходе наступают при меньших амплитудах входного сигнала, чем перегрузки во входных и выходных каскадах. В этом случае зависимость фронта сигнала на выходе от амплитуды входного сигнала имеет вид, представленный на рис. 5.22. Такую характеристику должна описывать макромодель, если она предназначена для моделирования при больших уровнях сигналов. Причем надо
отметить, что, например, для современных операционных усилителей большим входным сигналом, вызывающим перегрузки, является сигнал порядка десятков или сотен миливольт.
Рассмотрим теперь способы отражения в макромоделях нели-нейных эффектов. Если нет сведений о максимальных скоро-стях отклика для моделируемого усилителя, то нет возможности различать перегрузки на входе и выходе. Поэтому достаточно про-моделировать нелинейную передаточную характеристику усили-теля, отнеся эту нелинейность или ко входному, или к выходному каскадам.
Это можно сделать в рамках обычной макромодели, пример которой приведен на рис. 5.19. Достаточно ввести в один из зависимых источников, таблично заданный нелинейный коэффициент передачи. Если эта нелинейность введена до каскадов, отражающих частотные свойства усилителя, т.е. введена в первый источник тока, имеющий на рис. 5.19 крутизну S1, то это эквивалентно моделированию перегрузок во входном каскаде. В этом случае фронт выходного сигнала будет постоянным независимо от того, произошла перегрузка или нет. Спад вершины импульса также не будет зависеть от от наличия перегрузки.
Если нелинейность ввести после каскадов, отражающих частотные свойства, т.е. в зависимый источник К3, это будет эквивалентно моделированию перегрузок в выходном каскаде. В этом случае при возникновении перегрузок фронт на выходе будет уменьшаться с ростом амплитуды входного сигнала. Причем уменьшение будет неограниченным - при больших амплитудах фронт будет стремиться к нулю. Спад вершины импульса также будет зависеть от наличия и степени перегрузки. При подаче на вход длинного импульса большой амплитуды выходной сигнал
5.6. Формальные макроромодели аналоговы устройств |
187 |
ограничится на предельном уровне и этот уровень будет поддерживаться до тех пор, пока напряжение на индуктивности не спадет до величины, обеспечивающей переход в линейную область характеристик. Только после этого, если входной импульс еще не закончится, будет формироваться спад вершины.
Какой из двух рассмотренных вариантов более соответствует реальности, зависит от конкретной схемы моделируемого устройства. Чаще более соответствующим истине оказывается второй вариант, моделирующий ограничения на выходе.
Рассмотрим расчет параметров макромодели в этом варианте. Входным сигналом зависимого источника выходного напряжения, как видно из рис. 5.19, является величина Uвх S1 Rc S2 RL. Коэффициент пропорциональности S1 Rc S2 RL между Uвх и этой величиной можно выбрать произвольным. Чтобы не путаться с масштабами, удобно выбрать его равным 1. Тогда входной сигнал зависимого источника напряжения будет равен Uвх, а его выходной сигнал равен Uвых. Следовательно, коэффициент передачи источника просто должен повторять передаточную характеристику усилителя. Например, если передаточная характеристка усилителя аппроксимируется тремя отрезками прямых (см. рис. 5.20) и U+=10В, U-=- 10В, коэффициент усиления К0=1000, зависимый источник имеет имя E1, а узлы подключения имеют номера 3 - узел третьего каскада, 4 - узел подключения источника к сопротивлению Rвых, то описание зависимого источника может быть следующим:
E1 4 0 TABLE={V(3)} (-0.01 -10) (0.01 10) .
В этом описании -0.01 и 0.01 - соответственно значения U-/К0 и U+/К0, т.е входные сигналы в точках излома передаточной характеристики.
Теперь рассмотрим моделирование таких параметров усилителя, как максимальные скорости отклика Sот+ и Sот− для положительного и отрицательного выходных сигналов. Для этого надо промоделировать перегрузки во входном каскаде усилителя, т.е. отразить в макромодели ограничение сигнала до каскадов, описывающих частотные искажения. Значит, первый зависимый источник тока в макромодели рис. 20 надо сделать нелинейным, чтобы его передаточная характеристика имела вид, представленный на рис. 5.23, где I+ и I- - уровни ограничения, которые можно
рассчитать, исходя из максимальных скоростей отклика Sот+ и Sот− . Проведем подобный расчет в ранее принятых предположениях: S1=S2=1, Rc=RL=1.

188 |
5. Макромоделирование |
|
|
Проведем |
|
расчет |
для |
|||
|
|
максимальной |
скорости |
отклика |
||||
|
|
при |
положительном |
выходном |
||||
|
|
сигнале |
|
Sот+ . |
|
Для |
||
|
|
неинвертирующего |
усилителя |
|||||
|
|
она |
соответствует мгновенному |
|||||
|
|
переключению входного сигнала |
||||||
|
|
от большого |
отрицательного до |
|||||
|
|
большого |
положительного. При |
|||||
Рис. 5.23. Источник тока для моделирования |
большом отрицательном сигнале |
|||||||
выходной |
|
ток |
зависимого |
|||||
перегрузок на входе |
|
источника |
равен |
I-, |
а выходной |
|||
сигнал усилителя за счет |
ограничения на выходе |
равен |
U-. |
При |
подаче |
|||
большой ступеньки входного сигнала ток зависимого источника скачком изменяется до величины I+, а выходной сигнал усилителя после завершения переходных процессов установится равным U+. Чтобы эти утверждения были справедливы, должны выполняться соотношения К0 I-<U-<U+<К0 I+, соответствующие тому, что в усилителе ограничение по выходу наступает при меньших значениях входного сигнала, чем ограничение по входу. Сигнал UL, поступающий на вход выходного нелинейного зависимого источника напряжения, равен в области малых времен сигналу Uc, а последний при принятых условиях изменяется во времени по закону Rc I++Rc (I--I+) exp(-t/τв). Выходной сигнал начинает изменяться в момент, когда Uc попадает на границу линейной области, т.е. равен U-/К0, и кончает изменяться, когда Uc попадает на другую границу линейной области, т.е. равен U+/К0. Исходя из приведенного закона изменения Uc во времени, можно найти, что интервал полного изменения выходного сигнала макромодели на величину U=U+-U- равен
|
|
|
|
|
К I+ |
− U− |
|
|
|
|
|
|
|
t = τ |
в |
|
ln |
0 |
|
|
. |
|
|
|
|
|
|
К I+ |
− U+ |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
0 |
|
|
|
U и t в соотношение Sот+ = U/ t, можно найти |
||||
Подставив выражения для |
|||||||||||||
требуемую величину I+: |
|
|
|
] |
|
. |
|||||||
I+ = |
|
|
|
[ |
|
− U−) |
|
|
|
||||
|
U+ exp (U+ |
Sот+ |
τв |
|
− U− |
|
|||||||
|
|
|
|
{ |
[ |
|
− U−) |
|
|
] |
} |
|
|
|
|
К0 |
exp (U+ |
Sот+ |
τв |
|
− 1 |
|
|||||
В результате аналогичных выводов можно рассчитать и требуемую величину I-:

5.6. Формальные макроромодели аналоговы устройств |
189 |
I− = |
|
[ |
(U+ − U−) |
|
|
] |
− U+ |
. |
|
|
U− exp |
Sот− |
τв |
|
|
||||
|
|
{ |
[ |
|
|
] |
} |
|
|
|
К0 |
exp |
(U+ − U−) |
Sот− |
τв |
|
− 1 |
|
|
Мы рассмотрели моделирование эффектов, связанных с нелинейностями передаточной характеристики. Ранее в п. 5.6.2 было рассмотрено моделирование нелинейных входных ВАХ. Бывают, однако, в усилителях некоторые специфические нелинейные эффекты, связанные с нагрузкой и пока не рассмотренные. Первый из этих эффектов связан с ограничением выходного тока. В некоторых усилителях, в частности во многих операционных усилителях, приняты защитные меры против перегрузок по выходному току, предотвращающие выход схемы из строя при случайных коротких замыканиях на выходе или при слишком больших токах нагрузки. Осуществляется это обычно с помощью нелинейных обратных связей по току, резко увеличивающих выходное сопротивление схемы, если выходной ток превысил заданную предельную величину. Этот вид нелинейности определяется нагрузкой усилителя и, следовательно, однозначно не связан с нелинейностью коэффициента усиления, которая моделировалась ранее. Ограничение выходного тока легко моделируется в выходном каскаде макромодели с источником напряжения, изображенном на рис. 5.15б, если вместо линейного сопротивления Rвых поставить нелинейный двухполюсник с ограничениями тока на заданных уровнях. Характеристика подобного двухполюсника приводилась ранее в п. 5.2 на рис. 5.2в. Там же сказано, как реализуются подобные нелинейные двухполюсники в PSpice. В данном случае двухполюсник в линейной области должен иметь сопротивление, равное заданному значению Rвых, а предельные значения тока должны соответствовать установленным для моделируемого усилителя.
Другой вид нелинейности, связанной с нагрузкой, характерен для так называемых схем с открытым коллектором. В этих схемах выходным зажимом является оборванная коллекторная цепь выходного транзистора. К этому выходу должно подключаться внешнее сопротивление нагрузки Rн, питаемое от некоторого внешнего источника напряжения E. Это позволяет легко задавать любой требуемый коэффициент усиления выбором соответствующего сопротивления Rн. Однако при неудачном выборе Rн и E может оказаться, что выходной транзистор войдет в насыщение при небольшом входном сигнале или даже в отсутствие сигнала. Моделирование этого эффекта легко осуществить в выходном каскаде макромодели с источником тока, изображенном на рис. 5.15а, если вместо линейного сопротивления Rвых поставить нелинейный двухполюсник с ограничением напряжения на заданном уровне.

190 |
5. Макромоделирование |
Рассмотрим в качестве примера макромодель усилителя постоянного тока с открытым коллектором, для которого заданы: крутизна S0, входное сопротивление Rвх, верхняя граничная частота fв, выходное сопротивление Rвых, выходной ток в отсутствие сигнала I0 и указано, что выходное напряжение для предотвращения насыщения выходного транзистора должно быть положительным.
Возможная макромодель подобного усилителя представлена на рис. 5.24а. В этой макромодели нелинейность выходной цепи отражается нелинейным двухполюсником Dвых. На рис. 5.24б представлен другой вариант выходного каскада макромодели, в котором нелинейность выходной цепи отражается диодом D. Рассмотрим подробнее данную макромодель.
Рис. 5.24. Макромодель усилителя с открытым коллектором
Нелинейность ее передаточной характеристики отражается генератором тока S2 Uc. Зависимость тока этого источника от его входного напряжения Uc представлена на рис. 5.24в. При Uc=0 ток должен быть равен заданной величине I0. Наклон характеристики в линейной области определяется заданной крутизной S0. Однако, выходной ток не может становиться отрицательным, поскольку он является коллекторным током транзистора. Поэтому, начиная с точки, в которой ток спадает до нуля, он остается нулевым при дальнейшем уменьшении Uc.
