6.5 Случайные величины

Случайной величинойназывают такую величину, которая в результате испытания принимает одно и только одно из возможных своих значений, заранее неизвестное и зависящее от случайных обстоятельств, которые не всегда можно учесть. ОбозначаетсяX, Y, Z,…, возможные ее значения обозначаются.

Случайные величины бывают дискретныеинепрерывные. Дискретная случайная величина принимает отдельные изолированные возможные значения с определенными вероятностями.

Соответствие между возможными значениями дискретной случайной величины и их вероятностями называется закономилирядом распределения.

Пример.Бросаем игральную кость. Случайная величинаX– число выпавших очков, ее возможные значения 1, 2, 3, 4, 5, 6. Любое из этих значений появляется с вероятностью. Тогда:

X	1	2	3	4	5	6
P

– ряд распределения случайной величины.

Так как в каждом испытании случайная величина обязательно примет одно из возможных своих значений, то события образуют полную группу попарно несовместных событий, а поэтому.

Пример(см. ­задание 8). Составить закон распределения числа отказавших элементов прибора, если элементов три, а вероятность отказа каждого, независимо работающего элемента равна 0,2.

Пусть случайная величина X– число отказавших элементов, ее возможные значения:

,

,

,

,

.

Тогда закон распределения этой случайной величины принимает вид:

X	0	1	2	3
P	0,512	0,384	0,096	0,008

Контроль:

5.6 Числовые характеристики

Математическим ожиданиемдискретной случайной величины называется сумма произведений возможных значений случайной величины на вероятности этих возможных значений. Обозначается:

.

Математическое ожидание – это число, центр распределения случайной величины, – ее возможные значения расположены на оси левее и правее математического ожидания.

Дисперсиейдискретной случайной величины называется математическое ожидание квадрата отклонения этой случайной величины от своего математического ожидания.

.

Можно доказать, что

.

Этой формулой удобно пользоваться в расчетах. Дисперсия характеризует меру рассеяния возможных значений случайной величины относительно ее математического ожидания.

Средним квадратическим отклонениемназывается.

Пример. (см. задание 8). Дан ряд распределения случайной величины. Найти.

X	2	4	6	8	10
P

1) .

(В ваших заданиях может быть дробное число).

2) Найдем .

	4	16	36	64	100
P

.

Тогда:

,

.

Ниже приведены задания для контрольной работы.

Номер варианта соответствует последней цифре Вашего шифра. Из каждого задания необходимо выполнить пример, номер которого совпадает с номером Вашего варианта.

Каждую контрольную работу следует выполнять в отдельной тетради с указанием своего шифра и номера варианта. Условие задачи должно быть полностью переписано перед ее решением.

Отмеченные рецензентом ошибки необходимо исправить в конце работы, сделав работу над ошибками.

Зачтенные контрольные работы предъявляются студентом при сдаче зачета или экзамена.

ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ

IВычислить неопределенный интеграл

1.	а) ;	б) .
2.	а) ;		б) .
3.	а) ;		б) .
4.	а) ;		б) .
5.	а) ;		б) .
6.	а) ;		б) .
7.	а) ;		б) .
8.	а) ;		б) .
9.	а) ;		б) .
10.	а) ;		б) .

IIВычислить определенный интеграл

1.	.	6.	.
2.	.	7.	.
3.	.	8.	.
4.	.	9.	.
5.	.	10.	.

IIIВычислить площадь фигуры, ограниченной линиями

1.	,.	6.	,.
2.	,.	7.	,.
3.	,.	8.	,.
4.	,.	9.	,.
5.	,.	10.	,.

IVНайти общее решение дифференциального уравнения

1.	.	6.	.
2.	.	7.	.
3.	.	8.	.
4.	.	9.	.
5.	.	10.	.

VНайти общее решение дифференциального уравнения

1.	.	6.
2.	.	7.
3.	.	8.
4.	.	9.
5.	.	10.

VIНайти область сходимости степенного ряда

1.	.	6.	.
2.	.	7.	.
3.	.	8.	.
4.	.	9.	.
5.	.	10.	.

VIIРешить задачу

1. Устройство содержит два независимо работающих элемента, вероятности отказа которых за время Т соответственно равны 0,4 и 0,3. Найдите вероятность того, что за время Т откажет только один элемент.

2. Вероятность того, что сброшенная с самолета бомба попадет в цель, равна 0,03. вероятность того, что бомба разорвется, равна 0,99. Найти вероятность того, что цель будет уничтожена одной сброшенной бомбой.

3. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что наудачу взятое изделие стандартно, равна 0,7. Найдите вероятность того, что из двух проверенных изделий только одно окажется стандартным.

4. Баскетболист бросает мяч в корзину до первого попадания. Вероятность попадания при каждом броске равна 0,6. Какова вероятность того, что баскетболист попадет в корзину только с третьего раза?

5. В технической библиотеке имеются 70 книг по технике и 30 книг по математике. Зашедший в библиотеку читатель заказывает 3 книги. Какова вероятность того, что все они по одной тематике?

6. Два стрелка произвели по одному выстрелу по мишени. Вероятность того, что первый стрелок попал в цель, равна 0,7; для второго стрелка эта вероятность равна 0,8. Найти вероятность того, что хотя бы один из двух стрелков попал в цель.

7. Из слов «мама» и «дама» наугад выбирают по одной букве. Какова вероятность совпадения этих букв?

8. На колышек набрасывают кольца до первого попадания. Вероятность попадания при каждом броске равна 0,7. Какова вероятность, что будет израсходовано 4 кольца?

9. Студент пришел на экзамен, выучив лишь 20 вопросов из 25, имеющихся в программе. Преподаватель задает ему 3 вопроса. Какова вероятность, что студент знает все эти вопросы?

10. Вероятность попадания в цель при одном выстреле равна 0,6. Найти вероятность того, что из 5 выстрелов будет ровно 3 попадания.

VIIIРешить задачу

1. Баскетболист бросает мяч в корзину до первого попадания, но делает не более трех бросков. Составить закон распределения случайной величины Х – числа бросков, найти математическое ожидание М(Х) и дисперсию D(Х), если вероятность попадания при каждом броске равна 0,6.

2. Вероятность появления герба при одном подбрасывании монетки равна 0,5. Монета подбрасывается 3 раза. Составить закон распределения случайной величины Х – числа выпавших гербов, найти математическое ожидание М(Х) и дисперсию D(Х).

3. Рабочий обслуживает 3 станка. Вероятность того, что 1-й станок потребует внимание рабочего в течение часа, равна 0,6. Для 2-го станка эта вероятность равна 0,7; для 3-го станка – 0,8. Составить закон распределения случайной величины Х – числа станков, потребующих внимания рабочего в течение часа, найти математическое ожидание М(Х) и дисперсию D(Х).

4. Вероятность рождения мальчика равна 0,5. В семье 3 детей. Составить закон распределения случайной величины Х – числа мальчиков в этой семье, найти математическое ожидание М(Х) и дисперсию D(Х).

5. Имеется 3 заготовки для деталей. Вероятность изготовления годной детали из каждой заготовки 0,7. Составить закон распределения случайной величины Х – числа заготовок, оставшихся после изготовления годной детали, найти математическое ожидание М(Х) и дисперсию D(Х).

6. Вероятность того, что в библиотеке необходимая студенту книга свободна, равна 0,3. В городе три библиотеки. Составить закон распределения случайной величины Х – числа библиотек, которые посетит студент, найти математическое ожидание М(Х) и дисперсию D(Х).

7. Производится стрельба по мишени с вероятностью попадания в цель при каждом выстреле 0,6. Всего произведено 3 выстрела. Составить закон распределения случайной величины Х – числа попаданий в мишень, найти математическое ожидание М(Х) и дисперсию D(Х).

8. Прибор содержит три малонадежных элемента. Отказы элементов за некоторое время Т независимы, а их вероятности равны соответственно р₁=0,1, р₂=0,2, р₃=0,25. Составить закон распределения случайной величины Х – числа отказавших за время Т элементов, найти математическое ожидание М(Х) и дисперсиюD(Х).

9. Куплено 3 лотерейных билета. Вероятность выигрыша по одному билету равна 0,2. Составить закон распределения случайной величины Х – числа билетов, по которым выпал выигрыш, найти математическое ожидание М(Х) и дисперсию D(Х).

10. Необходимая студенту книга может быть свободна в одной из трех технических библиотек. Вероятность того, что студент получит книгу одинакова для всех библиотек и равна 0,3. Составить закон распределения случайной величины Х – числа библиотек, которые обошел студент пока не нашел нужную ему книгу, найти математическое ожидание М(Х) и дисперсию D(Х).

МАТЕМАТИКА
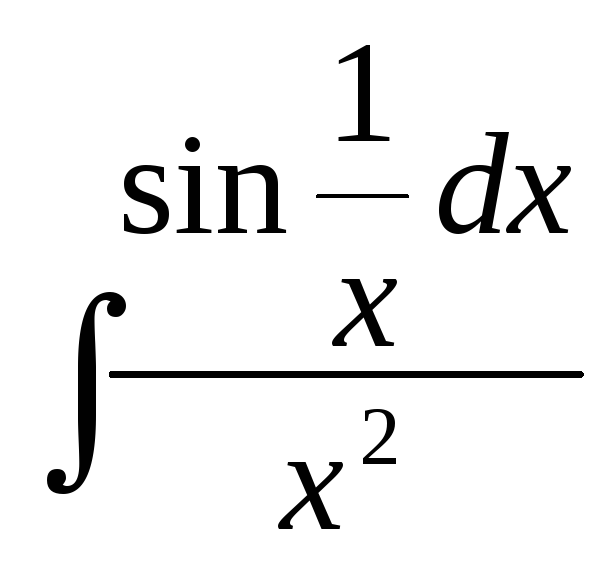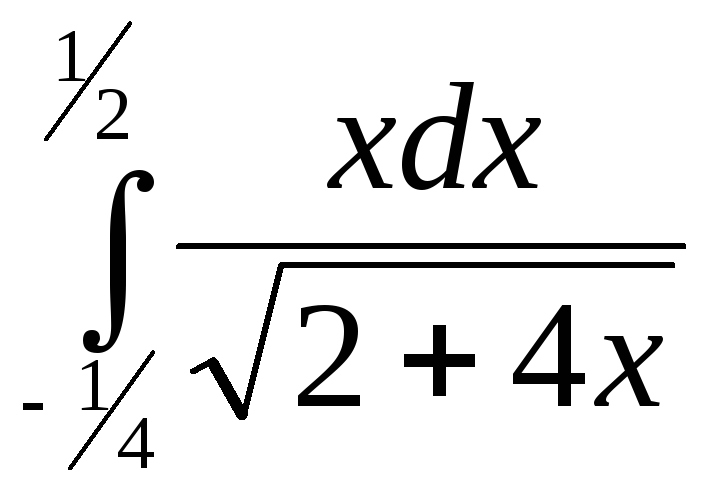