
- •IIчасть
- •Тема 1.Первообразная. Неопределенный интеграл, его свойства. Таблица основных интегралов. Непосредственное интегрирование. Интегрирование по частям и подстановкой.
- •1 Интегральное исчисление
- •1.1 Первообразная, неопределенный интеграл
- •2 Методы интегрирования
- •2.1 Метод подведения под знак дифференциала (устная замена переменной)
- •2.2 Метод письменной замены переменной (подстановки)
- •2.3 Метод интегрирования по частям
- •3 Определенный интеграл
- •3.1 Задача о площади.
- •3.2 Понятие определенного интеграла
- •3.3 Свойства определенного интеграла
- •4.3 Ду с разделяющимися переменными
- •4.4 Однородные функции
- •4.5 Однородные дифференциальные уравнения первого порядка
- •4.6 Линейные дифференциальные уравнения первого порядка
- •4.7 Линейные однородные д.У. Второго порядка с постоянными коэффициентами
- •4.8 Линейные неоднородные ду второго порядка с постоянными коэффициентами и специальной правой частью.
- •4.9 Системы дифференциальных уравнений
- •5.4 Знакопеременные ряды
- •5.5 Степенные ряды
- •6. Теория вероятностей
- •6.1 События. Операции над событиями
- •6.2 Вероятность события
- •6.3 Элементы комбинаторики
- •6.4 Основные теоремы.
- •6.5 Случайные величины
- •5.6 Числовые характеристики
- •Iiчасть
- •350072, Краснодар, ул. Московская, 2-а
4.8 Линейные неоднородные ду второго порядка с постоянными коэффициентами и специальной правой частью.
Это уравнение вида:
|
|
(3) |
где
![]()
![]() – многочлены степениnиmсоответственно.
– многочлены степениnиmсоответственно.
![]() – постоянные величины.
– постоянные величины.
Известно, что общее решение таких уравнений имеет вид
![]() ,
,
где
![]() – какое-либо частное решение неоднородного
уравнения (3),
– какое-либо частное решение неоднородного
уравнения (3),
![]() – общее решение соответствующего
однородного уравнения
– общее решение соответствующего
однородного уравнения
![]()
Частное решение уравнения (3) ищем в виде, подобном правой части:
|
|
(4) |
где
![]() многочленыk-той
степени с неизвестными коэффициентами,
определяемыми в процессе решения,k=max{n,m}.
многочленыk-той
степени с неизвестными коэффициентами,
определяемыми в процессе решения,k=max{n,m}.
При этом следует составить число
![]() ,
где
,
где![]() – коэффициент приxв показателе
– коэффициент приxв показателе![]() ,
,![]() – коэффициент приxв аргументе синуса или косинуса (если
один из них отсутствует). Если это число
– коэффициент приxв аргументе синуса или косинуса (если
один из них отсутствует). Если это число![]() не
является корнем характеристического
уравнения, то
не
является корнем характеристического
уравнения, то![]()
![]() в виде (4) оставляем без изменения, если
в виде (4) оставляем без изменения, если![]() есть корень кратностиs
(повторяетсяsраз),
то выбранный
есть корень кратностиs
(повторяетсяsраз),
то выбранный![]() домножаем на
домножаем на![]() .
.
Примеры
1) Если
![]() ,
то смотрим является ли корнем
характеристического уравнения число
,
то смотрим является ли корнем
характеристического уравнения число![]() ,
,
8 – многочлен нулевой степени, в общем
виде это некоторое число, т.е. выбираем
![]() .
.
2)![]()
![]()
![]() .
.
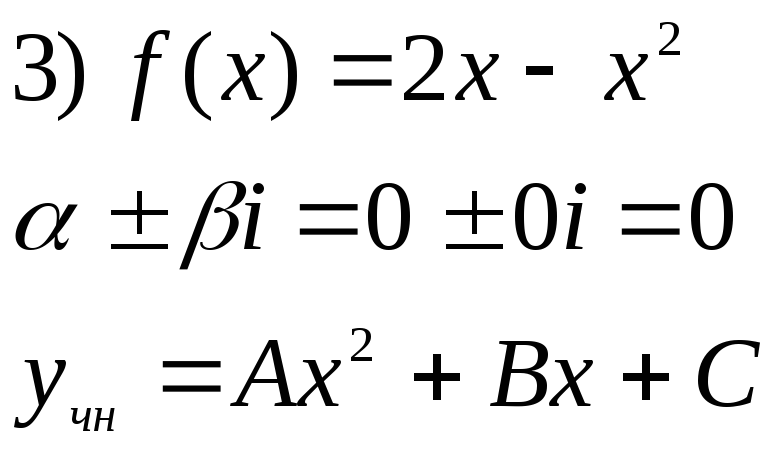
![]()
![]()
После предварительного выбора
![]() проверяем, является ли число
проверяем, является ли число![]() корнем характеристического уравнения.
Далее находим первую, вторую производную
корнем характеристического уравнения.
Далее находим первую, вторую производную![]() ,
подставляем их в первоначальное уравнение
и находимA, B,
C.
,
подставляем их в первоначальное уравнение
и находимA, B,
C.
Примеры (см. задание 5):
![]()
а) Найдем
![]() ,
решим соответствующее однородное
уравнение
,
решим соответствующее однородное
уравнение
![]() ,
составим характеристическое уравнение
,
составим характеристическое уравнение
![]() ,
,
![]() (корень
кратности 2 – повторяется 2 раза),
(корень
кратности 2 – повторяется 2 раза),
тогда
![]() -общее
решение соответствующего однородного
уравнения.
-общее
решение соответствующего однородного
уравнения.
б) Найдем
![]() .
Его будем искать в виде, подобном правой
части. Там
.
Его будем искать в виде, подобном правой
части. Там![]() -это
многочлен второй степени, в общем виде
это
-это
многочлен второй степени, в общем виде
это![]() ,
т.е.
,
т.е.
![]() .
.
Число
![]() не является корнем характеристического
уравнения, значит,
не является корнем характеристического
уравнения, значит,![]() оставим в выбранном виде. Теперь найдем
неизвестные коэффициенты
оставим в выбранном виде. Теперь найдем
неизвестные коэффициенты![]() .
Так как
.
Так как![]() – есть решение первоначального
дифференциального уравнения, то оно
обращает это уравнение в тождество.
Найдем
– есть решение первоначального
дифференциального уравнения, то оно
обращает это уравнение в тождество.
Найдем![]() и подставим в первоначальное уравнение
и подставим в первоначальное уравнение
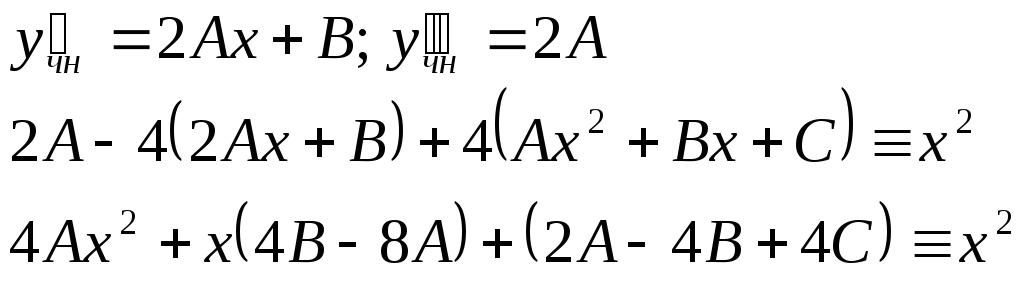
Два многочлена тождественно равны тогда
и только тогда, когда равны их коэффициенты
при одинаковых степенях неизвестного.
Приравняем коэффициенты при
![]() (свободный член) в обеих частях
(свободный член) в обеих частях
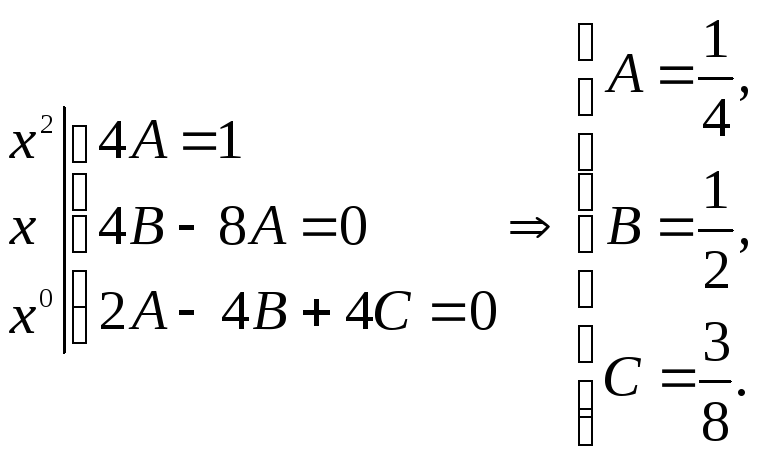
тогда
![]() .
.
Общее решение
![]() .
.
![]() ,
,
а)
![]() -решаем
соответствующее однородное уравнение.
Составим его характеристическое
уравнение.
-решаем
соответствующее однородное уравнение.
Составим его характеристическое
уравнение.
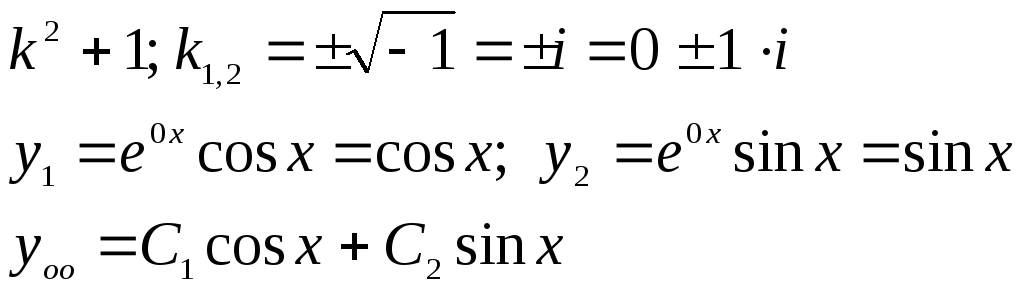
б)
![]() ,
,
![]() -является
корнем характеристического уравнения,
тогда
-является
корнем характеристического уравнения,
тогда![]() домножим наx , так
как пара
домножим наx , так
как пара![]() повторяется
один раз, тогда окончательно
повторяется
один раз, тогда окончательно
![]() .
.
Найдем AиB.
![]()
![]()
![]()
Подставим в первоначальное ДУ
![]()
![]()
Приравниваем коэффициенты при sin x и cos x
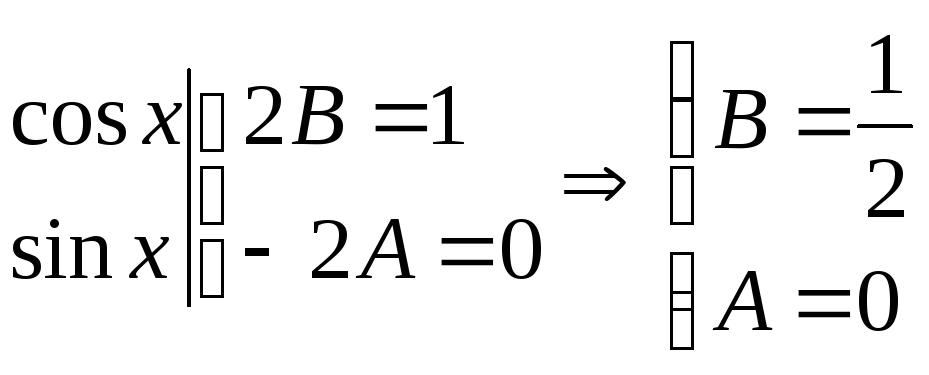
![]() ,
,
тогда
![]() .
.
Замечание.Если в правой части
отсутствуют![]() и
и![]() ,
частное решение ищем все равно в виде
суммы двух слагаемых.
,
частное решение ищем все равно в виде
суммы двух слагаемых.
4.9 Системы дифференциальных уравнений
Во многих прикладных задачах требуется определить сразу несколько функций, связанных между собой несколькими дифференциальными уравнениями. Совокупность таких уравнений называется системой ДУ
В дальнейшем ограничимся рассмотрением систем в нормальной форме (в таких системах правые части уравнений не содержат производных искомых функций).
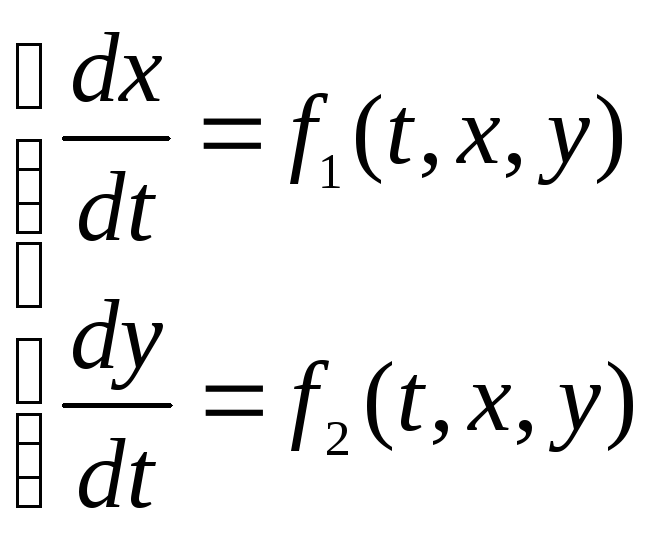
Для интегрирования этой системы применим
метод исключения, с помощью которого
данная система двух уравнений относительно
двух искомых функций
![]() сводится к одному уравнению второго
порядка относительно одной неизвестной
функции.
сводится к одному уравнению второго
порядка относительно одной неизвестной
функции.
Пример
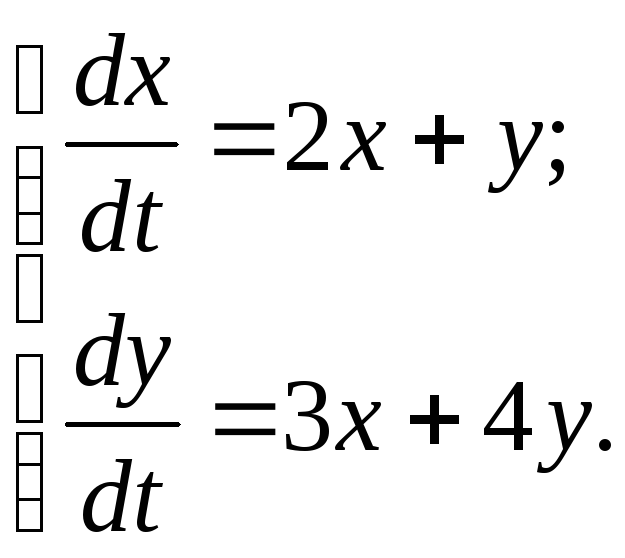
Запишем систему иначе:
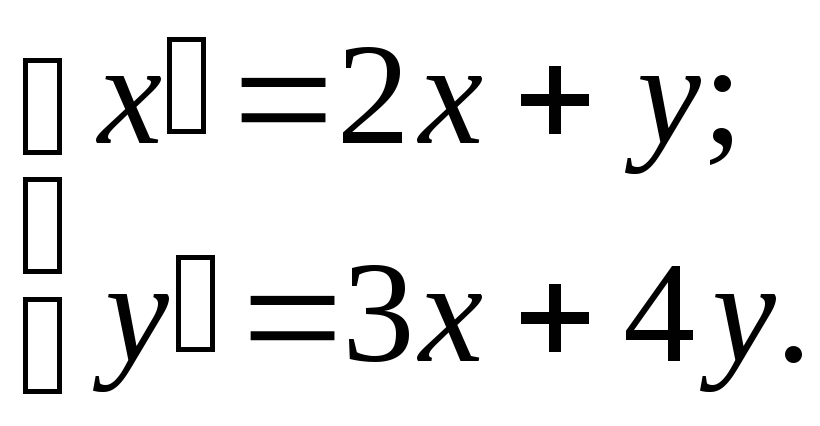
Из первого уравнения, например, выразим y(можно выразитьx):
![]()
Найдем производную:
![]()
Подставим во второе уравнение системы yи y’, выраженные черезx(t).
![]() ,
упростим:
,
упростим:
![]() ,
,
![]() .
.
Получили дифференциальное уравнение второго порядка с постоянными коэффициентами относительно неизвестной функции x(см. предыдущий раздел). Решим его.
![]() :
:
По теореме Виета:
![]()
Найдем другую неизвестную функцию:
![]() =
=
=3С1e5t-C2et,
т. е. решение системы имеет вид:
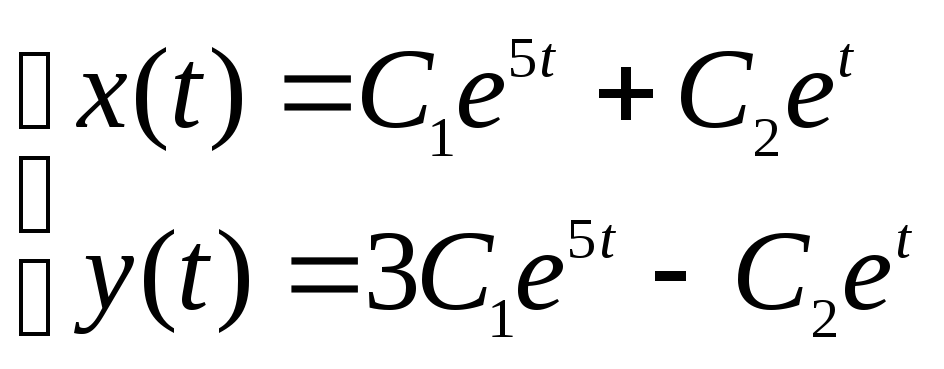 .
.
![]() – произвольные постоянные.
– произвольные постоянные.
5 Ряды
5.1 Ряд, сходимость, сумма.
Пусть дана последовательность чисел
![]()
Числовым рядомназывается выражение
![]() .
(1)
.
(1)
Сумма первых членов называется частичной суммой.
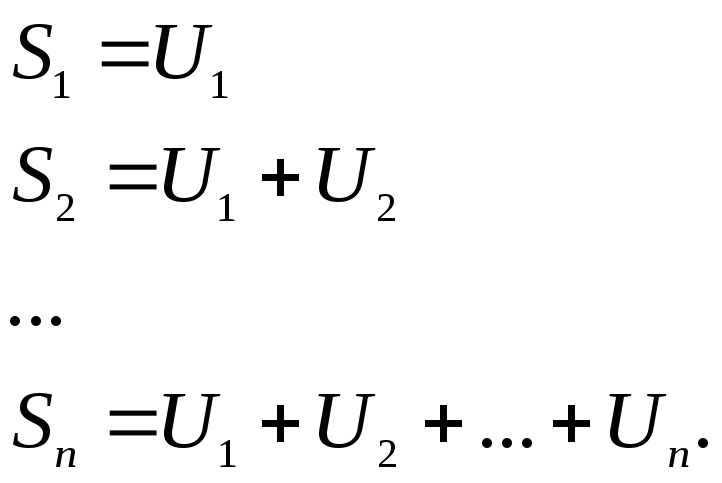
Частичные суммы образуют в свою очередь
последовательность
![]() ,
которая для одних рядов сходится, для
других – расходится.
,
которая для одних рядов сходится, для
других – расходится.
Ряд (1) называется сходящимся, если
существует конечный предел последовательности
частичных сумм![]() .
.
Sназывается суммой ряда. Если этот предел не существует или равен бесконечности, то ряд называетсярасходящимся.
Расходящиеся ряды суммы не имеют.
5.2 Свойства сходящихся числовых рядов.
Если ряд
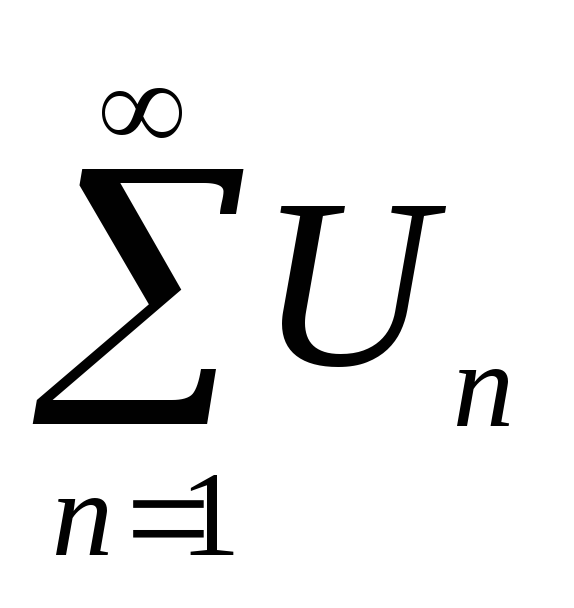 сходится
и имеет суммуS, то
ряд
сходится
и имеет суммуS, то
ряд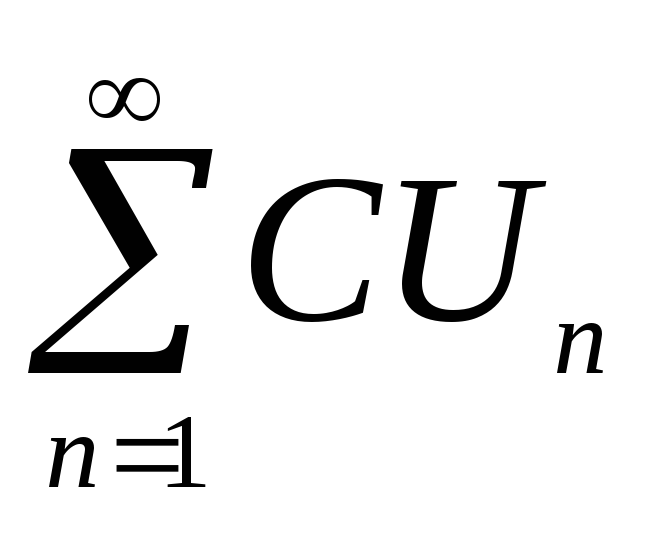 сходится и имеет суммуCS.
сходится и имеет суммуCS.Если ряды
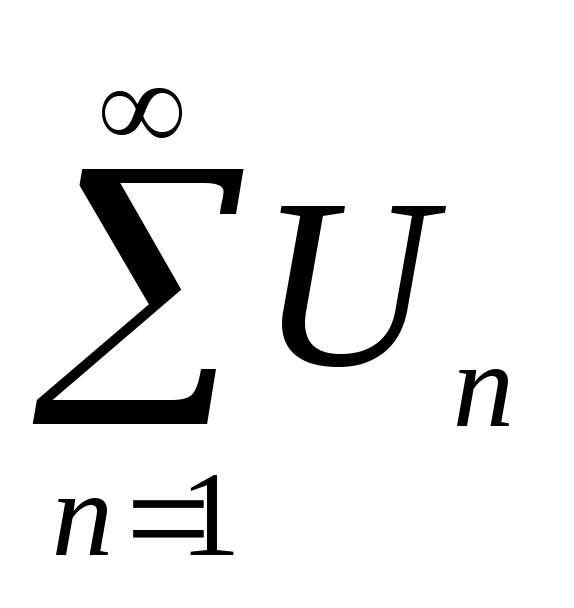 и
и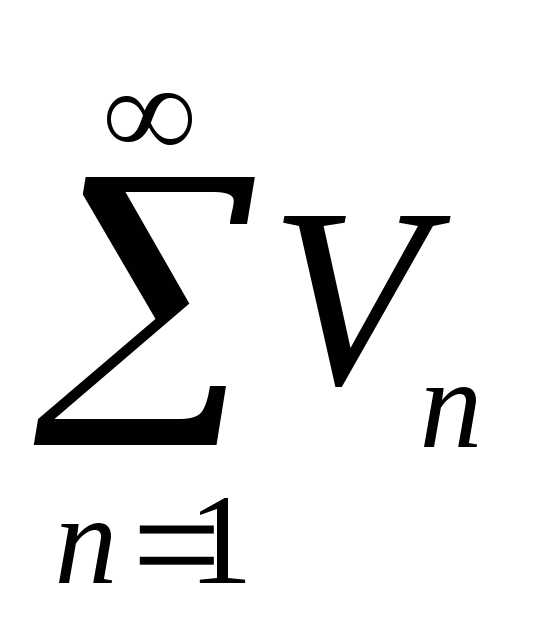 сходятся и имеют суммы
сходятся и имеют суммы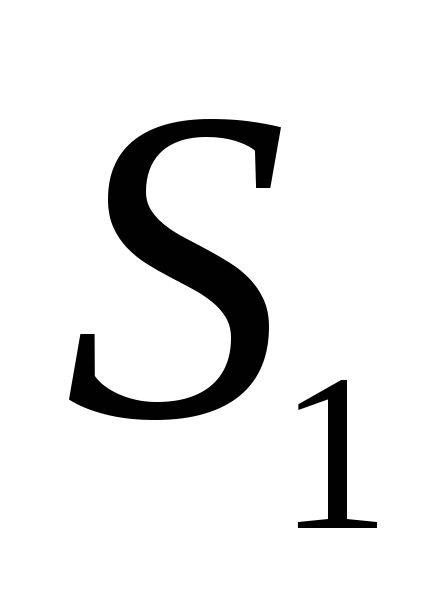 и
и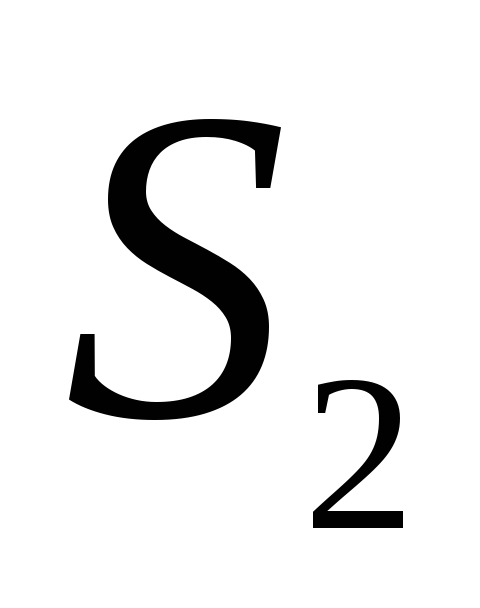 соответственно, то сходятся и ряды
соответственно, то сходятся и ряды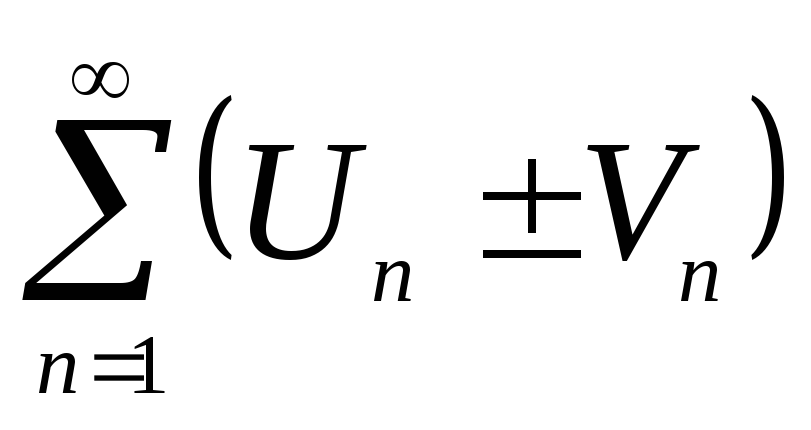 и имеют суммы
и имеют суммы .
.Добавление и отбрасывание конечного числа слагаемых не влияет на характер сходимости ряда.
5.3 Знакоположительные ряды. Необходимый признак сходимости.
Теорема. Если ряд
![]() сходится,
то
сходится,
то![]() .
.
Обратное утверждение неверно: если
![]() ,
то ряд может и сходиться и расходиться.
,
то ряд может и сходиться и расходиться.
Следствие(достаточный признак расходимости ряда):
Если
![]() ,
то ряд
,
то ряд![]() расходится.
расходится.
Примеры.
1)
![]() – ряд расходится.
– ряд расходится.
2)
![]() – ничего нельзя сказать о характере
сходимости ряда. Нужны дополнительные
исследования с помощью других признаков.
– ничего нельзя сказать о характере
сходимости ряда. Нужны дополнительные
исследования с помощью других признаков.
5.4 Достаточные признаки сходимости знакоположительных рядов.
1 Признак сравнения.
Даны два знакоположительных ряда
![]() и
и![]() .
Пусть, начиная с некоторогоn,
может быть и сn=1,
выполняется
.
Пусть, начиная с некоторогоn,
может быть и сn=1,
выполняется![]() ,
тогда:
,
тогда:
а) если
![]() сходится, то сходится и
сходится, то сходится и![]() ;
;
б) если
![]() расходится, то расходится и
расходится, то расходится и![]() .
.
Следствие: если существует![]() ,
конечное число, то ряды сходятся или
расходятся одновременно.
,
конечное число, то ряды сходятся или
расходятся одновременно.
Для использования этого признака удобно
выбирать ряд, составленный из членов
геометрической прогрессии
![]() ,
который сходится при
,
который сходится при![]() и расходится при
и расходится при![]() ,
а также обобщенный гармонический ряд
,
а также обобщенный гармонический ряд![]() ,
который сходится при
,
который сходится при![]() и расходится при
и расходится при![]() .
.
2 Признак Даламбера.
Пусть
![]() и существует
и существует![]() .
Тогда приq<1 ряд
сходится, при q>1
– расходится, приq=1
– сомнительный случай (нужно исследовать
с помощью других признаков).
.
Тогда приq<1 ряд
сходится, при q>1
– расходится, приq=1
– сомнительный случай (нужно исследовать
с помощью других признаков).
3 Радикальный признак Коши.
Пусть
![]() и существует
и существует![]() .
Тогда приp<1 ряд
сходится, при p>1
– расходится, приp=1
– сомнительный случай.
.
Тогда приp<1 ряд
сходится, при p>1
– расходится, приp=1
– сомнительный случай.
4 Интегральный признак Коши.
|
Дан
знакоположительный ряд
|
(1) |
Пусть
![]() – непрерывная, положительная, монотонно
убывающая функция, определенная при
– непрерывная, положительная, монотонно
убывающая функция, определенная при![]() и такова, что члены ряда являются
значениями функции при
и такова, что члены ряда являются
значениями функции при![]() ,
т. е.
,
т. е.![]() ,
,![]() ,
…,
,
…,![]() ,…,
тогда ряд (1) и несобственный интеграл
,…,
тогда ряд (1) и несобственный интеграл![]() сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
План исследования знакоположительных рядов
Находим
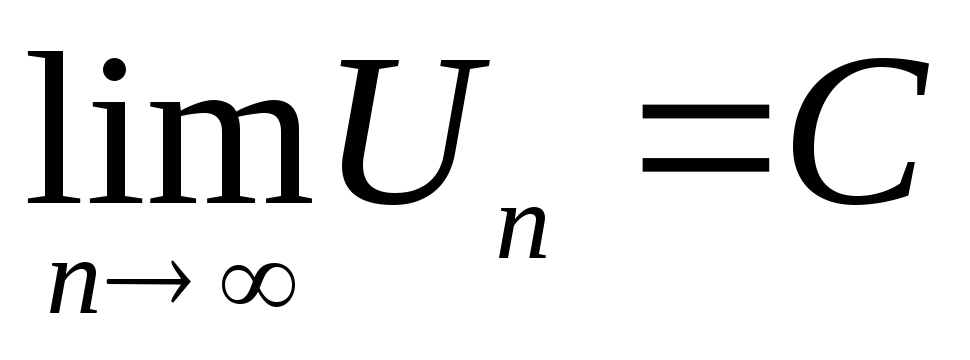 .
Если
.
Если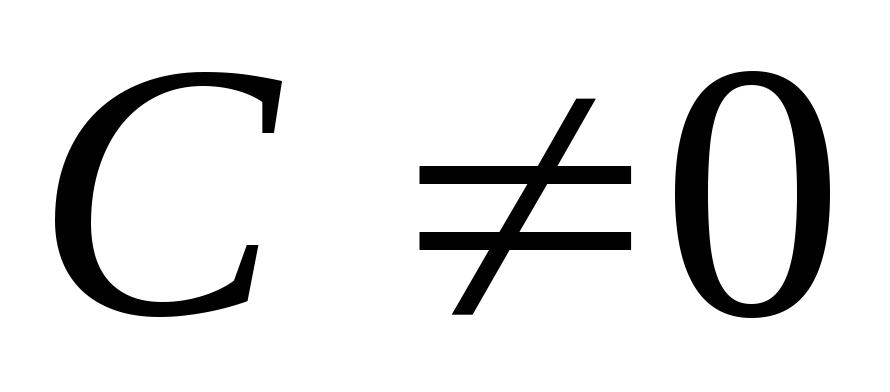 ,
то ряд расходится, исследование
закончено.
,
то ряд расходится, исследование
закончено.Если
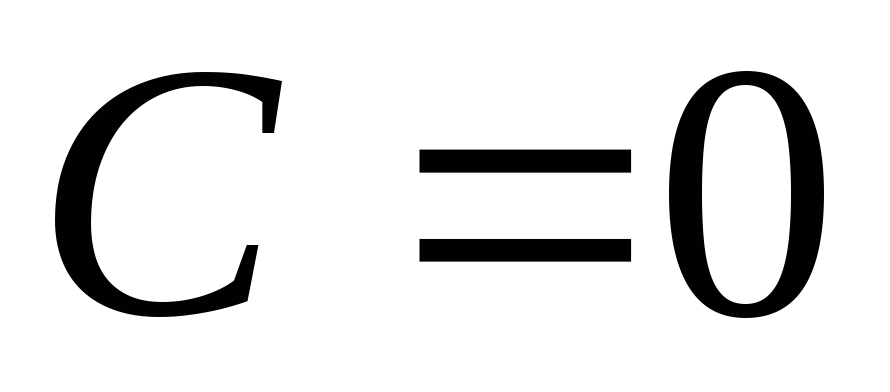 ,
применяем один (подходящий) из достаточных
признаков сходимости.
,
применяем один (подходящий) из достаточных
признаков сходимости.Делаем вывод о сходимости ряда.
Примеры.
1)
![]()
Напоминаем, что
![]() ;
0!=1;
;
0!=1;
![]() .
.
![]() – ряд, расходящийся по признаку Даламбера.
– ряд, расходящийся по признаку Даламбера.
2)
![]() – ряд сходится по радикальному признаку
Коши.
– ряд сходится по радикальному признаку
Коши.
3)
![]() сравним с
сравним с![]() – сходящимся (как обобщенный гармонический
– сходящимся (как обобщенный гармонический![]() приk>1). Используем
следствие из признака сравнения:
приk>1). Используем
следствие из признака сравнения:![]() – конечное, не равное нулю число, тогда
ряды ведут себя одинаково, т. е. сходятся.
– конечное, не равное нулю число, тогда
ряды ведут себя одинаково, т. е. сходятся.
