3.3 Свойства определенного интеграла

1) ; 2);

3) ; 4);

5) ;

6) Если , то;

Если , то.

Следствие. Если, то.

7) Если f(x)непрерывна на [a, b],m, M- ее соответственно наименьшее и наибольшее значение на [a, b], то справедлива оценка

8) (Теорема о среднем) . Если f(x)непрерывна на [a, b], то существует хотя бы одна точкатакая, что

3.4 Формула Ньютона-Лейбница

Пусть f(x)– непрерывна на [a, b],F(x) – первообразная функцииf(x) на [a,b], тогда определенный интеграл равен приращению первообразной (т.е. неопределенного интеграла) на этом отрезке:

Примеры

1) ;

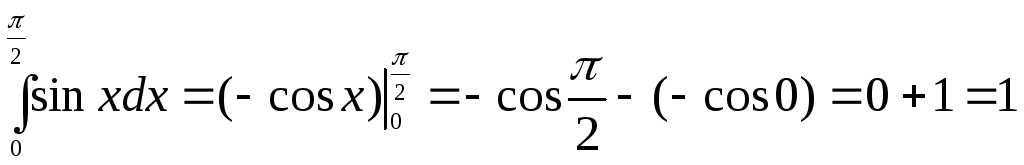2)

3.5 Интегрирование по частям

(см. интегрирование по частям в разделе "Неопределенный интеграл")

Формула интегрирования по частям для определенного интеграла имеет вид

Пример.

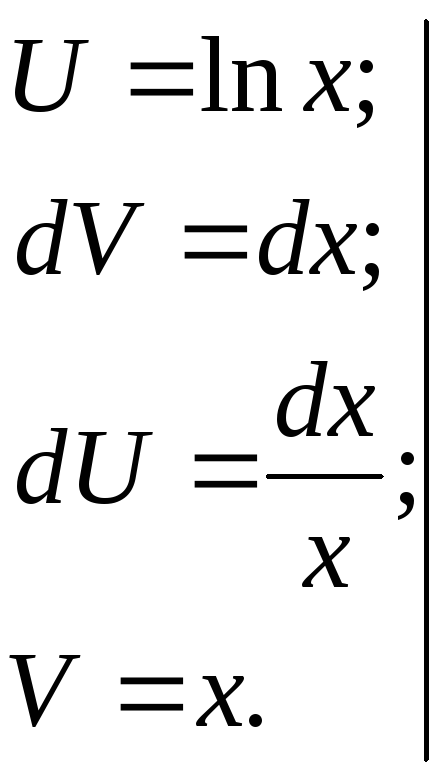
3.6 Замена переменной в определенном интеграле

Теорема. Пусть f(x)непрерывна на [a, b], введем подстановку. Если

1) непрерывны при,

2) при изменении t отдо, функцияизменяется отa доb,, то справедлива формула замены переменной:

Пример (см. задание 2):

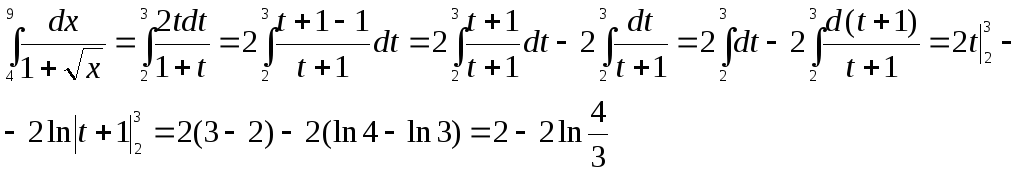
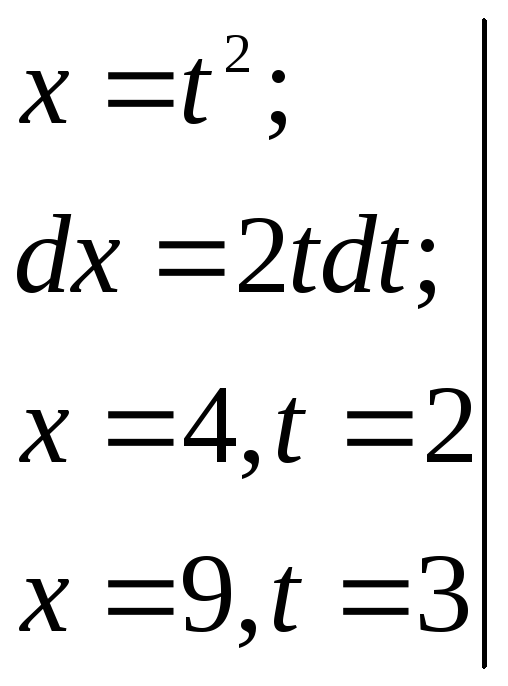
3.7 Вычисление площадей плоских фигур

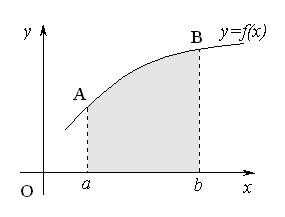– площадь криволинейной трапеции.

П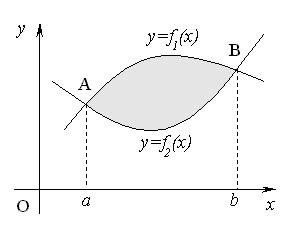лощадь фигуры, ограниченной линиями, находим по формуле

Эта формула остается справедливой при любом расположении рассматриваемой фигуры.

Пример(см. задание 3):

В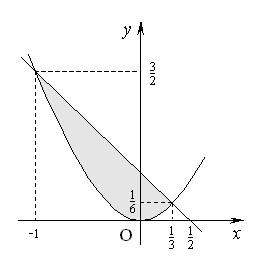ычислить площадь фигуры, ограниченной линиями: ,.

1) Найдем точки пересечения данных кривых.

;

;

;

;.

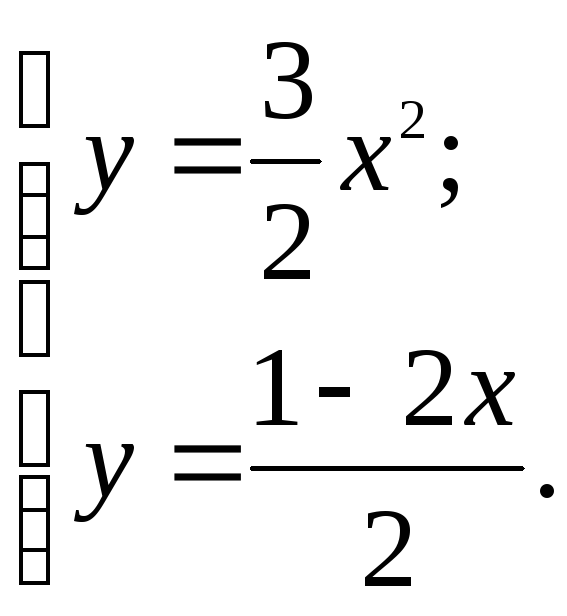
2) Построим графики данных функций.

(для прямой)

(парабола).

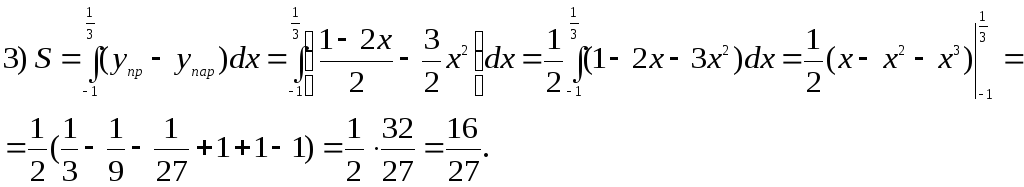4 Дифференциальные уравнения

4.1 Основные понятия

1. Дифференциальным уравнением (ДУ)называется уравнение, связывающее независимую переменную, искомую функцию и ее производные:

.

2. Наивысший порядок производной искомой функции, входящей в ДУ, называется порядком ДУ.

3. Решить ДУ – это значит найти все функции, которые ему удовлетворяют, т. е. при подстановке их в уравнение, оно обращается в тождество.

4. Нахождение решений ДУ называется интегрированием ДУ, график решения ДУ называетсяинтегральной кривой.

4.2 Дифференциальные уравнения 1 порядка

ДУ первого порядка называется уравнение, связывающее независимую переменную, искомую функцию и ее первую производную:

или в явном виде

(1)

Теорема Коши. Если в уравнении (1) функции ,определены и непрерывны в некоторой области изменения переменныхxиy , то какова бы ни была внутренняя точкаэтой области, ДУ имеет единственное решениеy=y(x) , удовлетворяющее начальным условиям

(2)

Геометрически это означает, что через каждую внутреннюю точку проходит единственная интегральная кривая.

Определение .Функцияy=y(x, С), зависящая от аргумента и произвольной постояннойС, называется общим решением ДУ, если

1) при любых значениях Сфункцияy =y(x, С) является решением уравнения (1);

2) Какова бы ни была точка , существует единственное значение постояннойтакое, что– есть решение (1), удовлетворяющее начальным условиям (2).

4.3 Ду с разделяющимися переменными

ДУ называется уравнением с разделяющимися переменными, если его можно представить в виде ,

где правая часть есть произведение сомножителей, каждый из которых является функцией только одной переменной.

Способ решения:разделение переменных по соответствующим дифференциалам (приdx должна стоять функция, зависящая отx, приdy– функция зависящая отy).

Пример:

1) ;

;

;

;

;

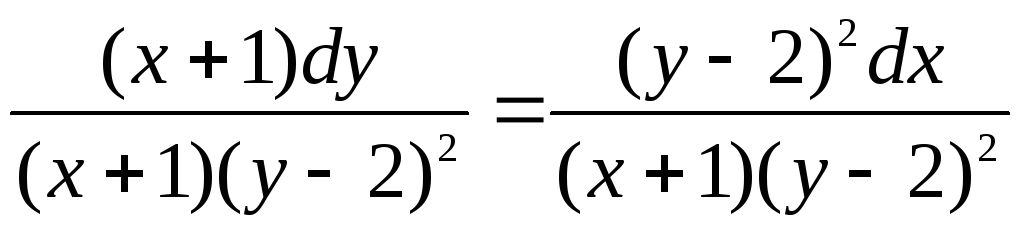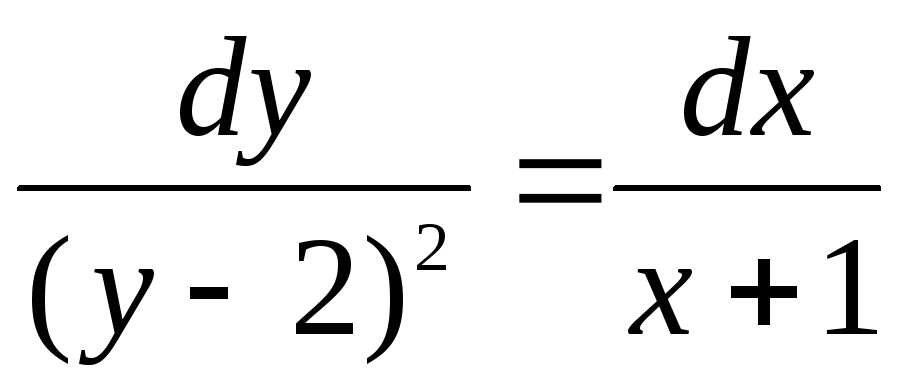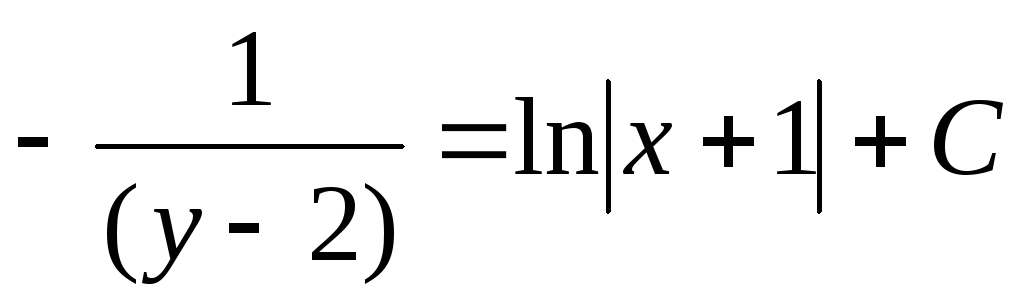– общее решение ДУ.

2) Найти частное решение уравнения , удовлетворяющее начальным условиям.

Найдем общее решение

– общее решение. Выделим из него частное, удовлетворяющее начальным условиям,.

;С=-22, тогда

– из всего семейства интегральных кривых (парабол) выделили одну, проходящую через заданную точку (4; 2).