2 Методы интегрирования

2.1 Метод подведения под знак дифференциала (устная замена переменной)

Если относительно данной переменной интеграл не является табличным, то в некоторых случаях его можно привести к табличному относительно новой переменной с помощью подведения под знак дифференциала нужной функции.

При этом удобно пользоваться следующими формулами, которые получаются из формул дифференцирования при прочтении их в обратном порядке:

…
,n≠-1

Примеры(см. задание 1а)

1) ;

2)

3)

2.2 Метод письменной замены переменной (подстановки)

План

1. Вводим новую переменную (подстановку)

2. Дифференцируем подстановку.

3. Вводим новую переменную в подынтегральное выражение.

4. Вычисляем интеграл.

5. Возвращаемся к старой переменной.

Примеры(см. задание 1а):

1)

.

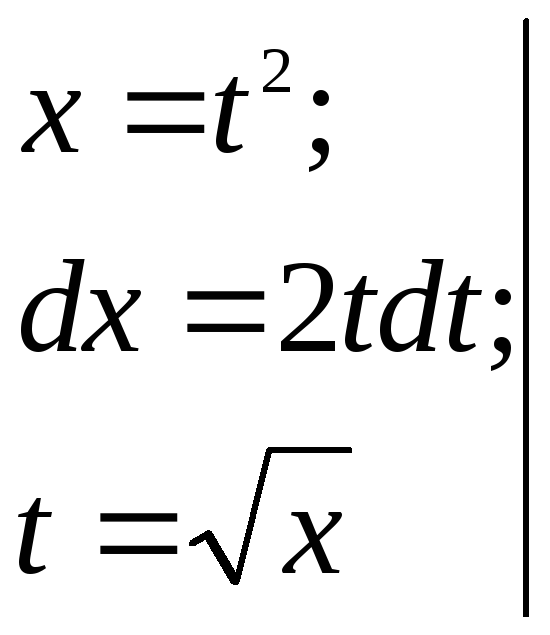
2)

.

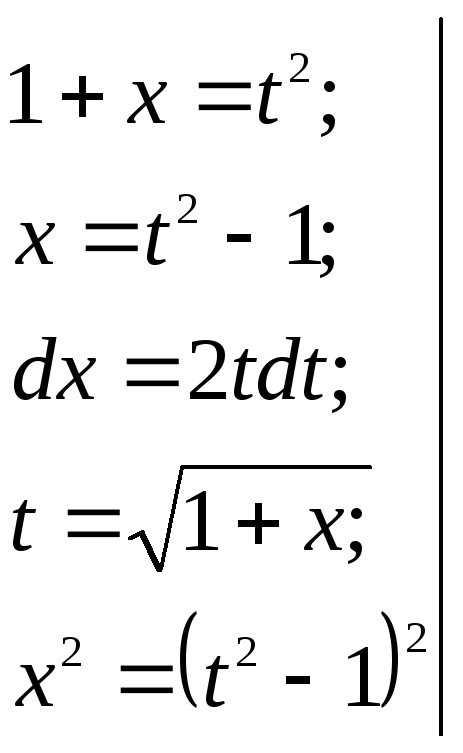
3) .

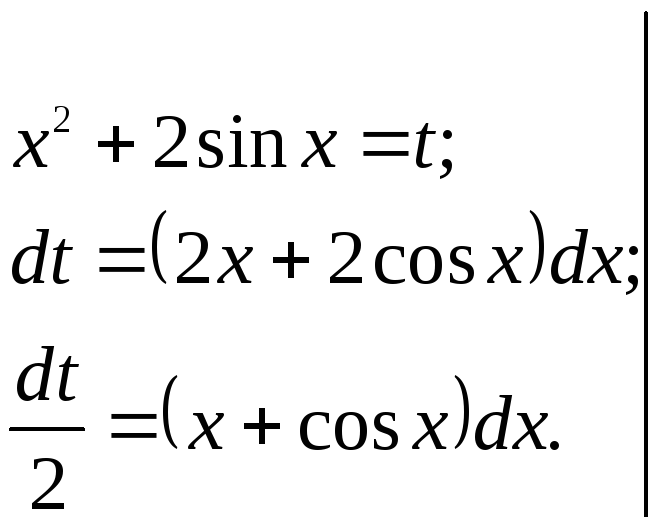
2.3 Метод интегрирования по частям

Этот метод применяют для интегралов вида:

а) ,,;

б) ,,,,;

в) ,;

где - многочлен.

Формула интегрирования по частям имеет вид:

.

1) Для интегралов типа а) принимают U =P(x), все остальное равноdV.

2) Для интегралов типа б) принимают dV =P(x)dx.

3) для интегралов типа в) за Uпринимают любую функцию, метод применяют дважды.

Примеры(см. задание 1б):

1) ;

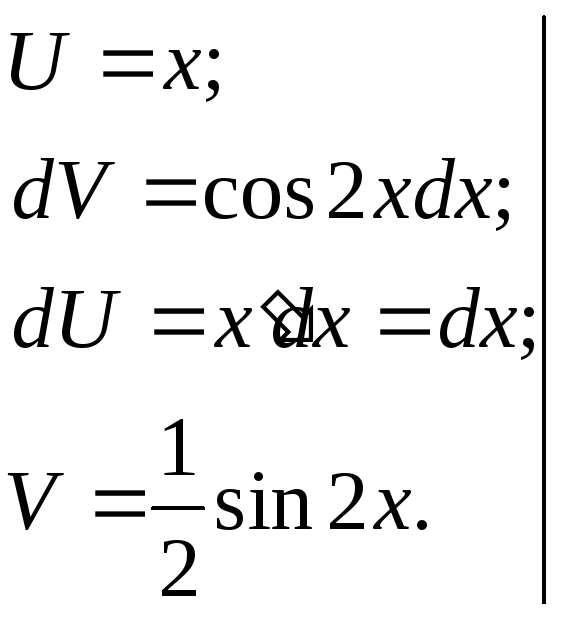
2)

;

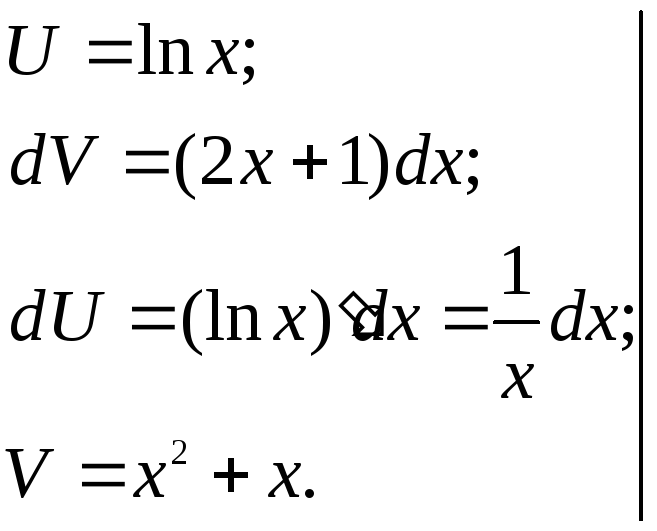
3)

.

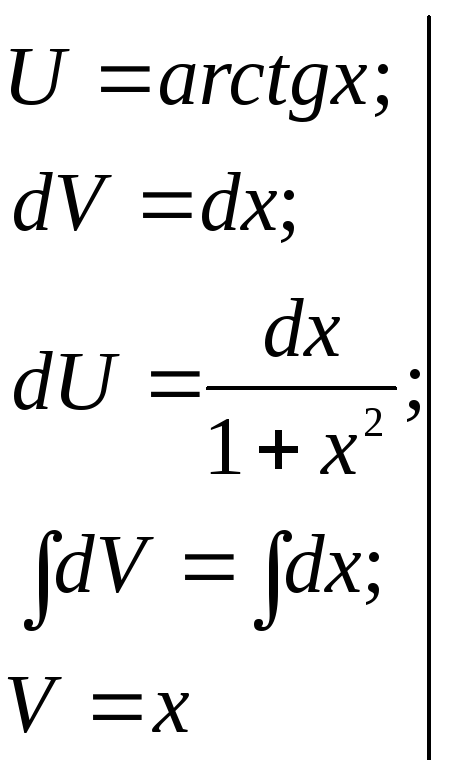
4) можно решение записать иначе:

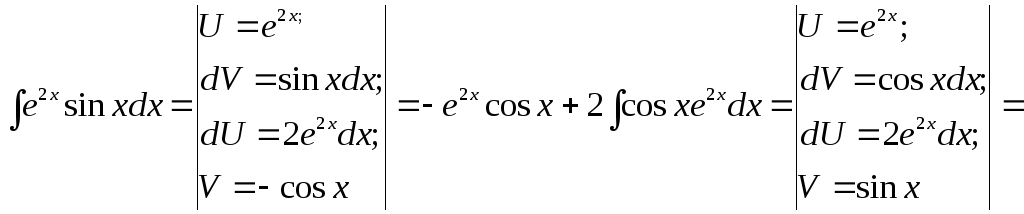
Получили первоначальный интеграл, обозначим его за y

;

;

+С.

3 Определенный интеграл

3.1 Задача о площади.

Вычислим площадь плоской фигуры, ограниченной графиком непрерывной, неотрицательной функции y=f(x), прямымиx=a, x=b, отрезком [a ,b]. Такая фигура называется криволинейной трапецией.

1) Разобьем отрезок [a, b] произвольным образом наnчастей точками. Получимnмаленьких отрезков с длинами;.

2) Через точки деления проведем вертикальные прямые. Трапеция разобьется на nтрапеций. На каждом из элементарных отрезков выберем произвольным образом по точке.

Найдем значения функции в этих точках

.

Примем эти ординаты за высоты прямоугольников.

3) Посчитаем, что площади маленьких криволинейных трапеций приближенно равны площадям прямоугольников с основаниями и высотами. Тогда

.

Чем мельче отрезки деления, тем точнее это равенство. За точное значение площади трапеции примем предел, к которому стремятся площади ступенчатых фигур при неограниченном увеличении числа отрезков деления и стремлении к нулю наибольшей из длин этих отрезков.

.

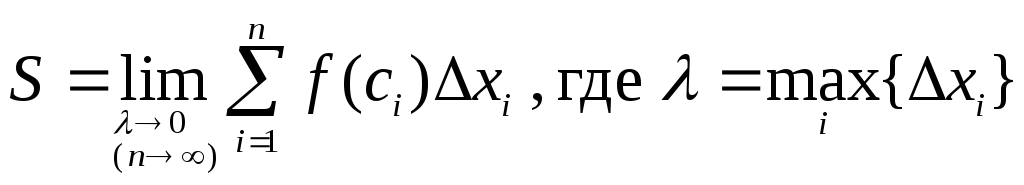3.2 Понятие определенного интеграла

К нахождению предела, рассмотренного в предыдущем пункте, приводит

ряд задач естествознания. Поэтому рассмотрим предел, отвлекаясь от конкретного смысла задачи.

Пусть на [a, b] задана произвольная функцияy=f(x).Применяя для нее схему предыдущей задачи, составим сумму произведений вида

.

Такая сумма называется интегральной суммой функции f(x) на [a, b]. Она

зависит от способа деления [a, b] на элементарные части и от выбора точек

на каждой из этих частей.

Определение. Если существует конечный предел последовательности интегральных сумм при, не зависящий от способа деления [a, b] и выбора точек, то этот предел (число) называется определенным интегралом от функцииf(x) на [a, b] и обозначается

_____________________________

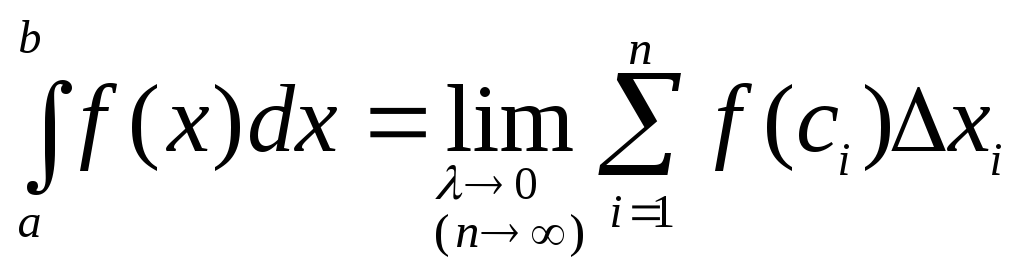
Возвращаясь к задаче о площади криволинейной трапеции, получаем

т.е. при определенный интеграл численно равен площади криволинейной трапеции. В этом состоит геометрический смысл определенного интеграла.

Теорема. Для любой непрерывной на [a,b] функции существует определенный интеграл.