
- •2. Понятие функции. Основные свойства функций.
- •3. Основные элементарные функции (степенная, показательная, логарифмическая, триго-нометрические, обратные тригонометрические).
- •2. Показательная функция:
- •3. Тригонометрические функции:
- •5. Логарифмическая функция.
- •5. Предел переменной величины и его свойства. Бесконечно малая и бесконечно большая величины.
- •6. Нахождение пределов. Замечательные пределы.
- •6.3. Замечательные пределы
- •8. Непрерывность функции в точке и на отрезке (2 определения)
- •9. Дифференциальное исчисление функции 1 переменной. Производная функции Основ-ные правила дифференцирования.
- •10. Производные степенных, тригонометрических, показательных, логарифмических функций. Производная сложной функции.
- •12. Экономический смысл производной. Использование понятия производной в экономике.
- •13. Дифференциал и его свойства. Приложение производной. Правило Лопиталя - Бернулли.
- •Глава 3. Приложения производной.
- •3.1. Правило Лопиталя-Бернулли.
- •I. Раскрытие неопределенностей вида и.
- •II. Раскрытие неопределенностей вида ,,,,.
- •14. Возрастание и убывание функции. Экстремум функции. Н. И д. Условия экстремума. Наибольшее и наименьшее значение функций.
- •15. Выпуклость и вогнутость функций. Н. И д. Условия выпуклости и вогнутости. Асимптоты функции.
- •16. Общая схема исследования функции.
- •17. Неопределенный интеграл и его свойства.
- •4.1. Свойства неопределенного интеграла.
- •18. Методы интегрирования: интегрирование разложением. Метод подстановки.
15. Выпуклость и вогнутость функций. Н. И д. Условия выпуклости и вогнутости. Асимптоты функции.
1.
Функция называетсявыпуклой вверх (вниз)на
промежутке, если для любых двух значенийx1,x2из этого промежутка выполняется
неравенство
называетсявыпуклой вверх (вниз)на
промежутке, если для любых двух значенийx1,x2из этого промежутка выполняется
неравенство
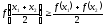
 .
.
Точки, разделяющие интервалы выпуклости, называются точками перегиба.
2.
Если вторая производная f"(x)
функции
f"(x)
функции
 положительна (отрицательна) на промежутке,
то функция являетсявыпуклой вниз
(вверх)на этом промежутке.
положительна (отрицательна) на промежутке,
то функция являетсявыпуклой вниз
(вверх)на этом промежутке.
3.
Еслиx0– точка
перегиба функции и
и f"(x0)существует, то
f"(x0)существует, то f"(x0)
= 0.
f"(x0)
= 0.
4.
Если вторая производнаяf"(x)меняет знак при переходе через точкуx0, то точкаx0
является точкой перегиба функции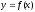 .
.
Таким образом, функция выпукла вниз на всем интервале (- ∞; 1), и точка х = 0 не является точкой перегиба. Нетрудно увидеть, что это точка экстремума (максимума) функции. Точках = 1 является точкой перегиба. На интервале (1; + ∞) функция является выпуклой вниз.
1. Прямаяl называетсяасимптотой графика функцииу = ƒ(х), если расстояние от точки(х, ƒ(х)) до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.
Асимптоты бывают вертикальными, горизонтальными и наклонными.
2. Прямаях = xо являетсявертикальной асимптотой графика
функции
у= ƒ(х), если хотя бы один из пределов ƒ(х) (правосторонний или левосторонний)
равен
ƒ(х) (правосторонний или левосторонний)
равен .
.
Прямая х = xо может быть вертикальной асимптотой функцииy= ƒ(х) в том случае, еслиxо – точка разрыва или граничная точка области определения.
3. Прямаяу = b являетсягоризонтальной асимптотой, еслиlimƒ(х) =b.

Если limƒ(х) =b, тоу = b — правосторонняя горизонтальная асимптота,
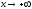
если limƒ(х) =b, то у =b—левосторонняя горизонтальная асимптота.

4.Если =k
=k 0
и
0
и
 =b, то прямаяy
= kx + bявляетсянаклонной асимптотой графика
функцииy = ƒ(х).
=b, то прямаяy
= kx + bявляетсянаклонной асимптотой графика
функцииy = ƒ(х).
16. Общая схема исследования функции.
Исследование функции можно проводить по следующей схеме:
1. Найти область существования функции.
2.
Исследовать изменения функции при
![]() ,
стремящемся к концам промежутков области
существования.
,
стремящемся к концам промежутков области
существования.
3. Найти промежутки возрастания и убывания функции, точки экстремума.
4. Вычислить значения экстремумов.
5. Определить интервалы выпуклости и вогнутости графика, найти точки перегиба.
6. Найти точки пересечения графика с координатными осями.
7. Найти асимптоты графика функции.
По результатам исследования можно построить математически грамотный эскиз ее графика.
Если исследуемая функция четная или нечетная, достаточно исследовать функцию и построить ее график для положительных значений аргумента из области определения.
Иногда порядок исследования целесообразно выбирать, исходя из конкретных особенностей данной функции.
17. Неопределенный интеграл и его свойства.
Неопределенным
интегралом от
непрерывной функции
 или от дифференциального выражения
или от дифференциального выражения называется общее
выражение для всех первообразных функций
называется общее
выражение для всех первообразных функций
 .Обозначение:
.Обозначение:
 (1)
(1)
где .Функция
.Функция
 называетсяподынтегральной
функцией, а
выражение
называетсяподынтегральной
функцией, а
выражение
 - подынтегральным
выражением.
- подынтегральным
выражением.
Свойства неопределенного интеграла.
1. Производная неопределенного интеграла равна подынтегральной функции; дифференциал неопределенного интеграла равен подынтегральному выражению:
 .
(2)
.
(2)
2.
Неопределенный интеграл от дифференциала
некоторой функции равен сумме этой
функции и произвольной постоянной:
 .(3)
.(3)
3. Постоянный множитель можно выносить за знак неопределенного интеграла:
 (4)
(4)
4. Неопределенный интеграл от алгебраический суммы непрерывных функций равен такой же алгебраической сумме неопределенных интегралов от слагаемых:

Таблица простейших неопределенных интегралов
 (5)
(5) (10)
(10)
 (5а)
(5а) (11)
(11)
 (5б)
(5б) (12)
(12)
 (6)
(6) (13)
(13)
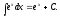 (7)
(7)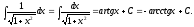 (14)
(14)
 (8)
(8) (15)
(15)
 (9)
(9)
