8. Непрерывность функции в точке и на отрезке (2 определения)

Функция называется непрерывной в точке, если в этой точке бесконечно малому приращению аргументасоответствует бесконечно малое приращение функции, т.е.

Функция называется непрерывной в точке, если при, предел функции существует и равен ее значению в точке, т.е.

Эти два определения непрерывности функции в точке равносильны друг другу.

Функция называется непрерывной в интервале, если она непрерывна во всех точках этого интервала.

9. Дифференциальное исчисление функции 1 переменной. Производная функции Основ-ные правила дифференцирования.

Производнойфункциив точкеназывается предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю: или

Если меняется, то предел (А) будет также меняться (для некоторыхон может не существовать), следовательно, производная данной функции есть некоторая функция.

Функция, имеющая конечную производную называется дифференцируемой. Операция нахождения производной называется дифференцированием.

Геометрическое значение производной.Производная функциядля каждого значенияравна угловому коэффициенту касательной к графику данной функции в соответствующей точке, т.е., где-- угол, образуемый касательной к графику с положительным направлением осипрямоугольной декартовой системы координат; этот угол является функцией аргумента. Механическое значение производной.Для функции, меняющейся со временем, производнаяесть скорость изменения функции в данный момент, т.е.где-- скорость измененияв момент.

Быстрота протекания физических, химических и других процессов выражается с помощью производной.

Если ,,-- дифференцируемые функции от, а-- постоянная величина, то имеют место следующие основные правила дифференцирования:

10. Производные степенных, тригонометрических, показательных, логарифмических функций. Производная сложной функции.

2.1. Производные степенных и тригонометрических функций.

Основные формулы:

2.2. Производная сложной функции.

Если и-- дифференцируемые функции своих аргументов, то производная сложной функциисуществует и равна произведению производной данной функциипо промежуточному аргументуна производную промежуточного аргументапо независимой переменной: или

2.3. Производные показательных и логарифмических функций.

Основные формулы:

Если -- дифференцируемая функция от, то формулы примут вид

2.4. Производные обратных тригонометрических функций.

Основные формулы:

Для сложных функций

11. Производные обратных тригонометрических функций. Производные высших порядков.

Производной второго порядкаили второй производной функцииназывается производная от ее производной. Она обозначается символами:

Аналогично определяются и обозначаются производные третьего, четвертого и других порядков:

Формула Лейбницадля производной-го порядка от произведения двух функций:

Производные п-го порядканазывается производная от производной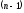-го порядка. Производные высших порядков вычисляются последовательным дифференцированием данной функции:

; …;.(7.28)

Если функция задана параметрически, то

; ; …;.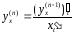