§ 2. Математическая модель случайного опыта.

Пусть G -некоторый случайный опыт, обладающий свойством устойчивости частот, т.е.

опыт, результаты которого не могут быть предсказаны однозначно до проведения испытаний;

возможны повторения испытания с первоначальным комплексом исходных данных сколь угодно большое число раз;

невозможно точное предсказание результата не только первого испытания, но и каждого последующего;

при неограниченном увеличении количества проведенных испытаний частота любого исхода стабилизируется, т.е. в определенном смысле близка к некоторой постоянной, называемой в дальнейшем вероятностью исхода.

Математическая модель такого случайного опыта Gназывается вероятностным пространством и обозначаетсяСокращенно~, где

- множество исходов опытаG;

-множество случайных событий, наблюдаемых в опытеG(класс подмножеств, называемый алгеброй или-алгеброй);

-вероятность случайных событий (вероятностная мера на измеримом пространстве). Связь вероятностной и теоретико-множественной терминологии отражена в таблице 1.

2.1. Алгебра событий.Рассмотрим случайный опытG,множество исходов которогоконечно. В такой модели событием назовем любое подмножество.

Пример.Случайный опыт G -выбор наудачу одной кости из полного набора костей домино. Возможные математические модели данного опыта:

Модель 1.

.

- совокупность всех подмножеств.

,(о вероятности см. ниже).

Модель 2.

гдеозначает, что выбран дубль, а- не дубль.

, где- невозможное событие;- достоверное событие.

Рассмотрим несколько возможных результатов опыта G:

1) А- выбран дубль.

2) В -сумма очков на выбранной кости равна 6.

В первой модели А = {(0.0), (1,1), (2,2), (3,3). (4.4), (5,5), (6,6)};

В={(0,6), (1.5), (2.4), (3,3)}.

Во второй модели А = -элементарное событие.В -не является событием, так как при появлении любого из исходовилимы не можем сказать, осуществлялся или нет результатВ.

Вернемся к наиболее содержательной первой модели. Так как события в модели являются подмножествами, то к ним можно применять все теоретико-множественные операции. Например,

В \ А= {(0,6). (1,5), (2,4)},,{(0,0), (1,1), (2,2), (3,3), (4.4), (5,5), (6,6), (0,6), (1.5), (2,4)},\A- не дубль.

Задачи для самостоятельного решения

1. Мишень состоит из десяти кругов, ограниченных концентрическими окружностями с радиусами . Событие-попадание в круг радиусапри одном выстреле по мишени. Описать множество исходов данного опыта. Что означают события,,,

.

2. Электрическая цепь состоит из элементов. Пусть событиеАозначает, что цепь безотказно работает в течение контрольного промежутка времени, а события- то же для-ого элемента;

А. Выразить событие А и через событиядля цепей с параллельным и последовательным соединением элементов.

В. Выразить через указанные ниже события:В -отказали все элементы,С -отказал хотя бы один элемент,D -безотказно работал один и только один из элементов,Е- отказали только два элемента..

3. Случайный опыт – испытание трех приборов. События: А- хотя бы один из трех проверяемых приборов бракованный;В -все приборы доброкачественные. Что означают событияa);b) c)d).

4. Опыт состоит в однократном бросании игральной кости. Описать возможные для данного опыта множества исходов. В каждой из предложенных моделей указать события: А - число очков, выпавших на верхней грани игральной кости, кратно трем; В -на верхней грани выпало нечетное число очков:С -число очков больше трех;D -число очков меньше семи;Е -число очков 0,5;F -число очков от 0,5 до 1,5. Установить пары совместных событий. Описать события

5. Пусть А и В -произвольные события, наблюдаемые в опытеG.

Проверить следующие равенства

a);

b)

6. Пусть число исходов равно Указать минимальное и максимальное возможные значения для числа всех случайных событий.

7. Может ли быть : a) число исходов конечно, а число всех случайных событий бесконечно; b) число всех случайных событий конечно, а число исходов бесконечно; c) число исходов больше, чем число всех событий.

В последующих пунктах мы рассмотрим примеры вероятностных пространств , объединенных интуитивным понятием равновозможности результатов опыта. .

2.2. Классическая схема(модель). Рассмотрим опытG,число возможных исходов которого конечнои все исходы равновозможны, т.е. непредпочтительны друг перед другом или имеют одинаковые шансы к появлению. Тогда

,

Обратимся к примеру п.2.1. В первой модели вероятность того, что выбранная наудачу кость окажется дублем

т.е. в длинной серии испытаний (каждый раз выбираем случайным образом одну кость из тщательно перемешанного полного набора) примерно четверная часть из них закончится появлением дубля.

В этой же модели

Во второй модели два возможных исхода опыта не являются равновоз-можными, т.е. в длинной серии независимых испытаний не дубль появляется чаще, чем дубль. В этой модели можно воспользоваться только статистическим способом задания вероятностей элементарных событий .

Поучительным примером невозможности выбора и обоснования вероятностной модели на основании априорных не физических соображений является разнообразие вероятностных распределений для различных способов размещения физических частиц по ячейкам, например, электронов по орбитам. До настоящего времени известно три модели:

Максвела-Больцмана - все размещенийразличных частиц поразличным ячейкам равновероятны.

Бозе-Энштейна - все способов заполненияразличных ячеекнеразличимыми частицами равновероятны (в статистической механике показано, что это предположение справедливо для фотонов, атомных ядер и атомов, содержащих четное число элементарных частиц)

Ферми-Дирака - все способов распределения равновероятны (эта модель применима к электронам, нейтронам и протонам).

Задачи для самостоятельного решения

1. Куб, все грани которого окрашены, распилен на тысячу кубиков одинакового размера. Полученные кубики тщательно перемешаны. Определить вероятность того, что наудачу извлеченный кубик будет иметь: а) три окрашенные грани; b) только две окрашенные грани; с) только одну окрашенную грань;d) не имеет окрашенных граней.

2. Ребенок играет с 10 буквами разрезной азбуки А,А,А,Е,И,К,М,М,Т,Т. Какова вероятность того, что при случайном расположении букв в ряд он получит слово МАТЕМАТИКА ?

Для решения задачи рекомендуем построить две модели: в одной все десять карточек считать различными, в другой - карточки с одинаковыми буквами неразличимы. Получив, естественно, одно и то же значение вероятности, объясните это.

3. У человека N ключей, из которых только один подходит к его двери. Он последовательно испытывает их, выбирая случайным образом (без возвращения), найти вероятность того, что этот процесс закончится на k-ом испытании.

4. Абонент забыл две последние цифры номера телефона и потому набрал их наудачу, помня лишь то, что а) эти цифры различны; в) эти цифры нечетные. Найти вероятность того, что номер набран правильно.

5. В шахматном турнире участвуют 20 человек, которые по жребию распределяются на две группы по 10 человек. Найти вероятность того, что а) двое наиболее сильных игроков будут играть в разных группах; в) четверо наиболее сильных игроков попадут по два в разные группы.

6. Из урны, содержащей шары с номерами 1,2,.....9, пять раз наугад вынимают шар и каждый раз возвращают обратно. Найти вероятность того, что из номеров вынутых шаров можно составить возрастающую последовательность.

7. Десять студентов договорились о поездке за город, но не договорились о вагоне. Поэтому каждый из них выбирает для себя вагон случайным образом. Найти вероятность того, что а) все попадут в разные вагоны; в) все попадут в первый вагон; с) все попадут в один вагон, считая число вагонов .

8. В отделение связи поступило шесть телеграмм. Телеграммы случайным образом распределяют по четырем каналам, причем каждая телеграмма может быть передана по любому из четырех каналов. Найти вероятность того, что на первый канал попадут три телеграммы, на второй - две телеграммы, на третий - одна телеграмма и четвертый канал не будет загружен.

2.3. Геометрическая схема.Геометрическое определение вероятности обобщает классическое на случай бесконечного множества исходов, считаянекоторым подмножествомRⁿ , например, промежуток дляп= 1; круг, прямоугольник для= 2; шар, параллелепипед для= 3. Математическое описание опытаG -бросание случайным образом идеальной частицы (точки) в областьили выбор наудачу точки из области- принято называть геометрической схемой. В этой модели- ограниченное множествоRⁿ, имеющееn-мерный объем ( меру Лебега),и;- класс измеримых подмножеств;- вероятностная мера наи вероятность попадания точки в область А считается равной

.

Таким образом, вероятность попадания "случайно брошенной"точки в определенное подмножествопропорциональна мере этого подмножества и не зависит от его расположения и формы.

Пример. В круг единичного радиуса бросается случайным образом точка. Найти вероятность того, что эта точка попадает в круг радиуса 0,5: а) с тем же центром; в) с центром в точке С и ОС =OD,гдеO- центр окружности,OD-радиус окружности.

a) 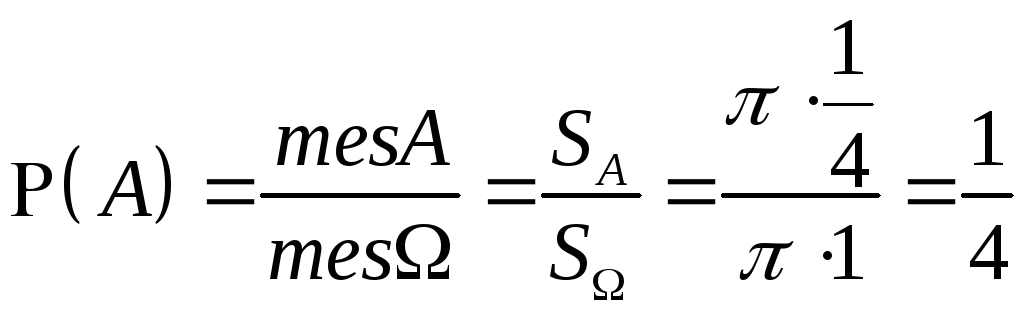;b)

т.е. очевидно , так как

Задачи для самостоятельного решения.

1. Поступления каждого из двух сигналов в приемник равновозможны и независимы в любой момент промежутка времени Т. Определить вероятность того, что приемник будет "забит", что происходит в том случае, когда промежуток времени между моментами поступления обоих сигналов меньше .

2. Два парохода должны в течение суток подойти к одному и тому же причалу. Определить вероятность того, что одному из пароходов придется ожидать освобождения причала, если время стоянки первого парохода один час, второго - два часа, и каждый из них независимо друг от друга появляется у причала в случайный момент времени в течение данных суток.

3. В круг вписан квадрат. Точка наудачу бросается в круг. Найти вероятность того, что она попадет в квадрат.

4. В квадрат с вершинами (0;0), (0;1), (1;0), (1;1) наудачу брошена точка М. Пусть будут ее координаты. Найти вероятность того, что корни уравнения= 0 а) действительны; в) оба положительны.

5. Какова вероятность того, что сумма двух независимым образом наугад взятых положительных чисел, каждое из которых не больше единицы, не превзойдет единицы, а их произведение будет не больше 2/9?

6. Пусть иопределены так же, как в задаче 4. Длянайти вероятность того, что: а); в); c) ;

d) ; е).