36

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Теория вероятностей

Пособие для студентов по специальностям 010100 и 510100

ВОРОНЕЖ

2003

Утверждено научно-методическим советом математического

факультета ( 2 сентября 2003г., протокол №2 )

Составители: Михайлова И. В.

Баркова Л. Н.

Пособие подготовлено на кафедре уравнений в частных производных и теории вероятностей математического факультета Воронежского государственного университета.

Рекомендуется для студентов 3 курса дневного и 5 курса вечернего отделений.

§1. Элементы комбинаторики.

Центральной задачей комбинаторной теории (комбинаторики) можно считать задачу размещения (распределения) объектов в соответствии со специальными правилами. Если эти правила просты, то основным в этой задаче является подсчет числа возможностей для осуществления искомого размещения. Задачи такого типа принято называть задачами перечисления. Если же правила распределения объектов сложны, то главной проблемой становится вопрос существования таких распределений и нахождения методов их осуществления.

Нас будут интересовать только перечислительные задачи. В том случае, когда интересующих нас вариантов размещения немного, мы можем все эти варианты перебрать. В других случаях это невозможно из-за большого числа вариантов и тогда на помощь приходят основные правила подсчета: принципы

(правила) сложения и умножения.

Принцип суммы.Пусть множество А содержитпэлементов, а множествоB - kэлементов, причем. Тогда множествосодержитп+kэлементов.

Замечание 1. Если обозначить - число элементов множества А, то в формализованном виде правило суммы можно сформулировать следующим образом: еслито .

Замечание 2. При решении задач удобной бывает следующая формулировка: элемент из А или элемент из Вможно выбратьп+ kчислом способов, гдеп -количество способов выбрать элемент из А,k –элемент изВ .

Принцип произведения.Пусть заданы два множестваи.Тогда декартово произведение

содержит элементов, т.е., если

Подводя итог сказанному, подчеркнем, что если выбирается или то или другое, то нужно применять правило суммы, а если и то, и другое, то правило произведения. Например, на тарелке лежат 5 яблок и 3 груши. Если выбираем яблоко или грушу, то число способов 5+3=8. Если выбираем и яблоко, и грушу, то 5 • 3 == 15.

Замечание 1. Пусть необходимо выполнить одно за другим какие-то действий (2). Если первое действие можно выполнитьспособами, после чего второеспособами, после чего и т.д. -ое действие можновыполнить способами,то вседействий можно выполнитьспособами.

Замечание 2. Если на выполнение какого-либо из действий наложены ограничения (т.е. некоторое действие необходимо выполнить по-особому, не так, как другие), то обычно бывает целесообразно подсчет начинать именно с этого действия.

Пример. В автомашине семь мест. Сколькими способами семь человек могут сесть в эту машину, если занять место водителя могут только трое из них?

Решение. Для размещения семи человек в автомашине необходимо выполнить семь действий (заполнить семь мест), то есть = 7. На одно из этих действий (заполнение места водителя) наложены ограничения. Поэтому это действие будем считать первым и тогда= 3, после чего заполнение любого из оставшихся можно осуществить= 6 способами и т.д. Заполнение последнего места можно выполнить только одним способом, то есть= 1. Согласно принципу умножения, все семь действий можно выполнить 3способами.

Принципы умножения и сложения дают нам общий метод решения задач. Помимо этого общего метода, полезными оказываются следующие понятия и формулы.

Рассмотрим сначала следующую задачу. Из трех букв нужно выбрать какие-то две. Сколько способов выбора? Оказывается здесь спрятаны четыре задачи.

Считать ли abиодинаковыми вариантами? Если порядок выбора существенен, то варианты выбора будем называть размещениями. Если порядок выбора безразличен, то варианты выбора будем называть сочетаниями.

Другой важный вопрос - возможны ли повторения? То есть можем ли мы выбирать два раза одну какую-либо букву? Если да, то мы говорим о размещениях или сочетаниях с повторениями, а если нет - то о размещениях или сочетаниях без повторений.

Итак, пусть - множество произвольной природы, содержащеепэлементов, n.

Размещениями без повторенийили просторазмещениямииз nэлементов множестваВпо элементов будем называть всевозможные упорядоченные подмножестваВ, содержащиеразличных элементов множестваВ.Число размещений из nпо

ипри

Размещениями с повторениемизпэлементов множествапоэлементов будем называть упорядоченные наборы поэлементов множества ,среди которых могут быть и одинаковые элементы. Число таких размещений

.

Перестановкамиизпэлементов множестваВназовем размещения изпэлементов множествапоnэлементов. Число перестановок изпразличных элементов.

Сочетаниямиизn элементов множествапоэлементов называются подмножества множестваВ,содержащиеразличных элементов множестваВ.Число сочетаний из nпо

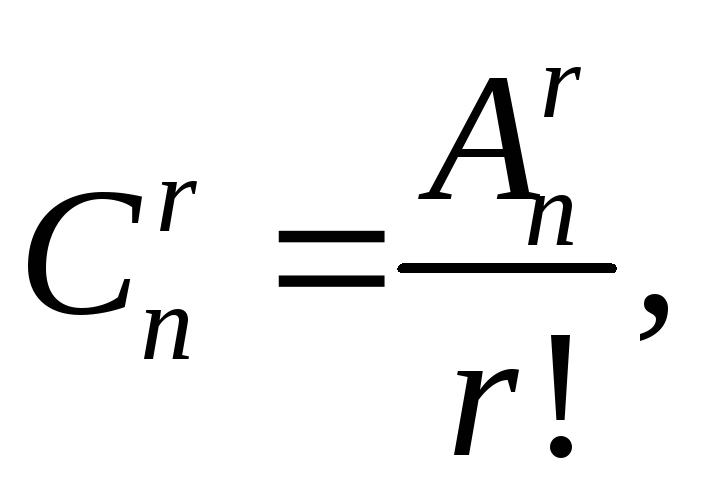
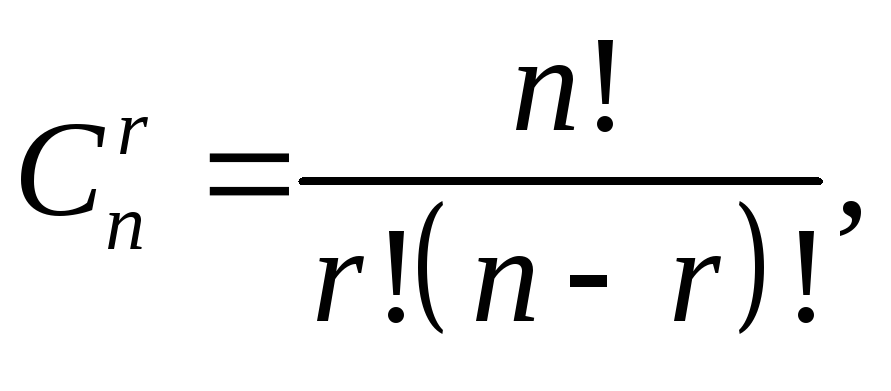
Сочетаниями с повторениямиизпэлементов множестваВ по элементов называются всевозможные наборы, содержащиеэлементов множестваВ, среди которых могут быть одинаковые. Число сочетаний с повторениями из по

,

Замечания. Различные размещения из пэлементов множестваВ поэлементов (с повторениями и без повторений) отличаются друг от друга составом (хотя бы одним из элементов) или порядком (роль элементов в размещении различна).

Различные перестановки из n элементов множестваВотличаются друг от друга только порядком следования элементов.

Различные сочетания из n элементов множестваВ поэлементов отличаются друг от друга только составом.

Возвратимся к поставленной задаче и найдем число способов выбора двух букв из указанных.

В том случае, когда осуществляется выбор без возвращения выбранного элемента в исходную совокупность, т.е. речь идет о размещениях без повторений, число вариантов равно Перечислим их.

Если же осуществляется выбор с возвращением, то число вариантов равно. Это - .

В другом случае, если порядок букв не существенен и буквы не повторяются, то, используя формулу сочетаний без повторений, имеем

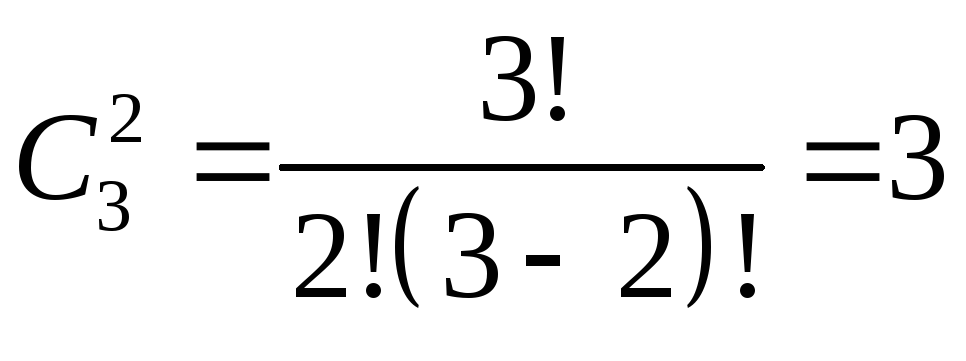. Здесь варианты.

И, наконец, число сочетаний с повторениями 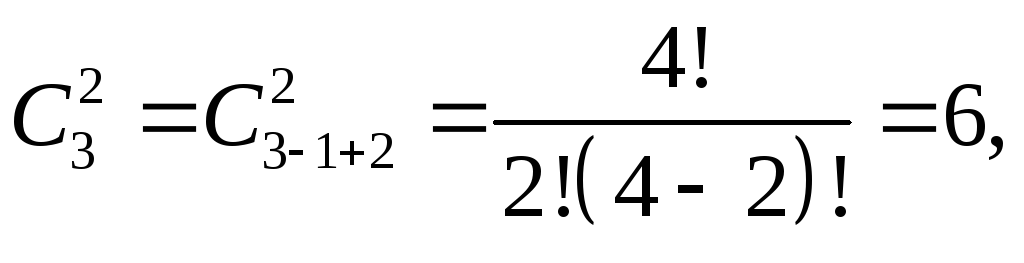а варианты:.

Задачи для самостоятельного решения

1. На окружности выбрано десять точек. Сколько существует хорд с концами в этих точках? Сколько ненулевых векторов с концами в этих точках? Сколько векторов с концами в этих точках? Сколько треугольников с вершинами в этих точках? Сколько выпуклых пятиугольников, выпуклых десятиугольников?

2. Даны три карточки с цифрами 1,2,3. Сколько чисел можно составить из этих трех карточек?

3. Десять спортсменов разыгрывают золотую, серебряную и бронзовую медали. Сколькими способами эти медали могут быть распределены между спортсменами?

4. Сколькими способами девушек могут образовать хоровод?

5. Сколькими способами различных шаров можно разместить поразличным ячейкам, предполагая, что а) в ячейке может быть более одного шара; в) не может быть более одного шара.

6. Сколько различных подмножеств, включая само множество и пустое, можно выделить из множества, содержащего элементов.

7. В розыгрыше лотереи участвуют 3 человека. Каждому из них присвоен порядковый номер. Участники лотереи должны вытащить одну карточку из трех с номерами 1,2,3. Призы выдаются тем, кто вытащит карточку со своим порядковым номером. Каково число вариантов, в которых выигрыш только у одного участника лотереи? В которых ни один не выигрывает? Ответить на вопросы для произвольного

8. Сколько пятибуквенных слов (перестановок), каждое из которых состоит из трех согласных и двух гласных, можно образовать из букв слова УРАВНЕНИЕ.