1.3. Представлення вектора в дск, сск і дск

Вектор в довільній СК має стандартне представлення:

.

Оскільки вектор є інваріантним об’єктом, то між його компонентами в різних СК можна встановити певні співвідношення. Розглянемо їх на прикладах ДСК і ССК, та ДСК і ЦСК.

В першому випадку

. (1.9)

Для встановлення зв’язку між декартовими () і сферичними () компонентами вектора, скористаємось наступним загальним способом. Помножимо обидві частини останнього рівняння на орт. Внаслідок ортогональності ортів ДСК отримуємо:

. (1.10)

Так само виражаються через сферичні компоненти і .

Для побудови оберненого перетворення, ліву і праву частини (1.9) потрібно множити на один з ортів ССК. Знову ж таки, внаслідок ортогональності ССК будемо отримувати рівняння вигляду:

. (1.11)

Як бачимо, в обох випадках потрібно знати скалярні добутки між всіма парами ортів ДСК і ССК.

а) Проекція ортів ССК на орти ДСК. З означення кутів і Рис.3 випливає, що

(1.12)

Перше з цих співвідношень встановлюється безпосередньо. Для орту враховується, що він утворює з віссю кут, а азимутальний кут є таким же, як і для орту. Орт лежить у площині, паралельній до (), і утворює з віссюкут.

б) Обернена побудова: проекція ортів ДСК на орти ССК. Перейдемо до допоміжної ДСК, вісь співпадає з віссю, а вісіілежать в площині () і утворюють кутиз осямиі. Зрозуміло, що площина () співпадає з меридіональною площиною ССК і мають місце наступні співвідношення:

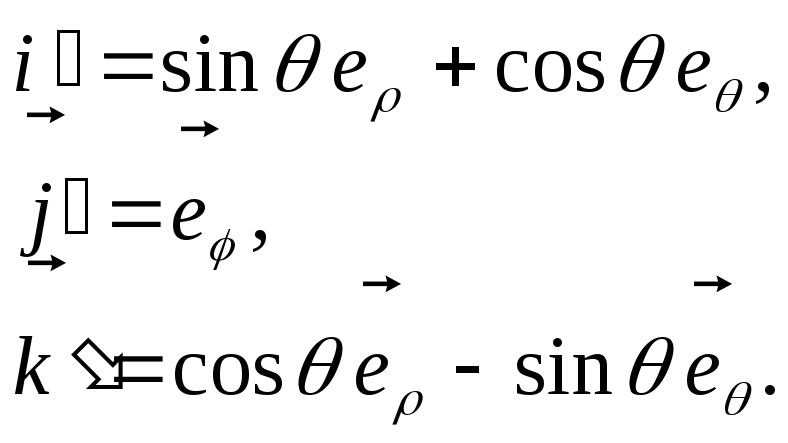
Разом з тим, орти () пов’язані з допоміжними ортами () стандартним перетворенням, яке відповідає повороту навколо вісіна кут:

Комбінуючи ці перетворення, знаходимо:

(1.13)

в) Зв'язок декартових координат вектора з його сферичними координатами. Виходячи зі співвідношень типу (1.10), отримуємо:

(1.14)

г) Зв'язок сферичних координат вектора з його декартовими координатами.

З (1.11) і (1.13) випливає:

(1.15)

д) Відмітимо, що матриця оберненого перетворення () співпадає з транспонованою матрицеюпрямого перетворення ():

,

що безпосередньо випливає з їх означення (див. (1.10) і (1.11)):

і .

Формули (1.14) і (1.15) повністю узгоджуються з цією умовою. Фактично, формули (1.15) можна було б побудувати, виходячи тільки з цієї умови і вигляду матриці , яка задається перетвореннями (1.14).

е) Прямі і обернені перетворення в ЦСК. Тут вихідною є формула:

.

Орти перетворюються за формулами:

Матриці іпрямого і оберненого перетворень компонентів вектору, які визначаються співвідношеннями:і, дорівнюють:

і .

Вони задовольняють тим самим вимогам симетрії, що і для ССК.