
Для студентов / Методички / (1)Методичка - ВЕД / ЧI_Р4
.docРОЗДІЛ 4. ЕЛЕКТРОСТАТИКА
4.1 Загальні положення
У загальному випадку рівняння Максвела у вакуумі мають вигляд:
![]()
![]()
(4.1)


У випадку, коли поля не залежать від часу система розпадається на дві підсистеми. Перша з них описує постійне електричне поле (електростатика):
![]() (4.2)
(4.2)
![]() .
.
Друга - постійне магнітне поле (магнітостатика):
![]() (4.3)
(4.3)

Друге з рівнянь (4.2) можна тотожно задовільнити, якщо покласти:
![]() . (4.4)
. (4.4)
Тоді
маємо одне рівняння, загальний розв’язок
якого включає довільні константи. Для
визначення цих констант треба
використовувати граничні умови. Для
нормальних та тангенціальних складових
вектора
![]() :
:
![]() ;
;
(4.5)
![]() ,
,
де
![]() -поверхнева
густина заряду.
-поверхнева
густина заряду.
Враховуючи (4.4), першому рівнянню системи (4.2) можна придати вигляд:
![]() . (4.6)
. (4.6)
Це є рівняння Пуасона. Його розв’язок включає довільні константи. Граничні умови:
![]() (4.7)
(4.7)
 ,
,
де
![]() -
похідна за напрямком, який перпендикулярний
до границі.
-
похідна за напрямком, який перпендикулярний
до границі.
4.2 Методи розв’язування задач электростатики
До методів точного розв’язування задач електростатики належать такі методи:
-
безпосереднє підсумування;
-
використання теореми Остроградського-Гауса;
-
інтегрування рівняння Пуассона;
-
інтегрування рівнянь Максвела;
Задача.
Сфера радіуса
 рівномірно заряджена. Густина поверхневого
заряду
рівномірно заряджена. Густина поверхневого
заряду
 .
Визначити потенціал і напруженість
електричного поля, яке утворюється
сферою.
Одержати
розв’язок
усіма методами.
.
Визначити потенціал і напруженість
електричного поля, яке утворюється
сферою.
Одержати
розв’язок
усіма методами.
1) безпосереднє підсумування.
а) для просторового розподілу заряду:
 (4.8)
(4.8)
де
![]() -просторова
густина заряду.
-просторова
густина заряду.
б) для поверхневого розподілу заряду:
 , (4.9)
, (4.9)
де
![]() -поверхнева
густина заряду.
-поверхнева
густина заряду.
в) для лінійних зарядів:
 , (4.10)
, (4.10)
де
![]() -
лінійна густина зарядів.
-
лінійна густина зарядів.
г) для точкових зарядів:
 . (4.11)
. (4.11)
В даній задачі реалізується випадок (б).
Інтегрування виконується по всій поверхні сфери. Відповідно з симетрією задачі інтегрування слід виконувати в сферичних координатах. Справедливі співвідношення:
![]() ;
;
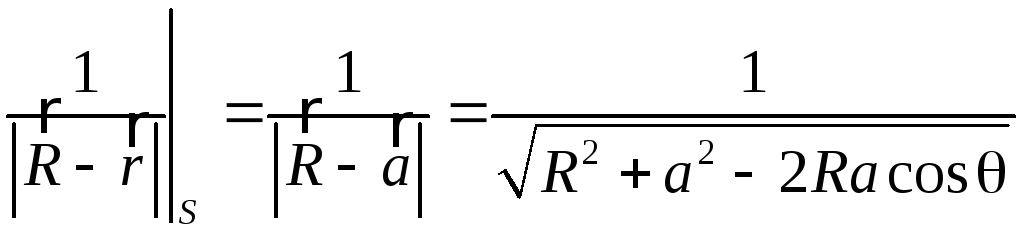 .
.
Безпосереднім інтегруванням одержуємо:

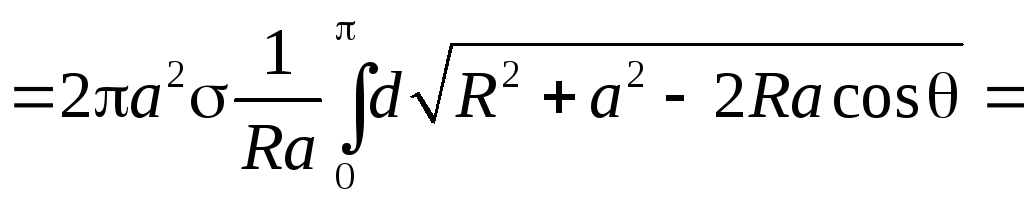
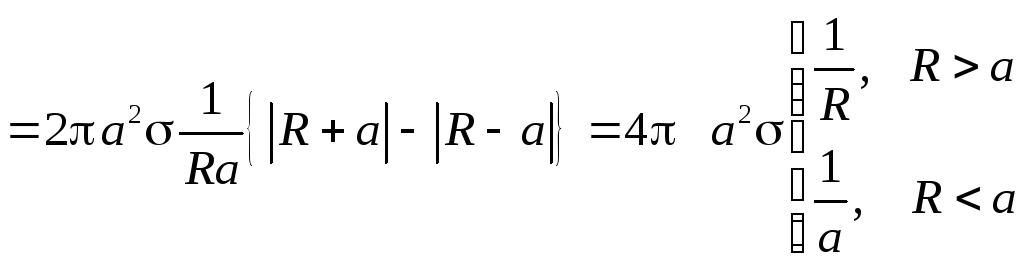 .
.
Враховуючи,
що
![]() ,
остаточно одержуємо:
,
остаточно одержуємо:
 . (4.12)
. (4.12)
Використовуючи
(4.4), та співвідношення:
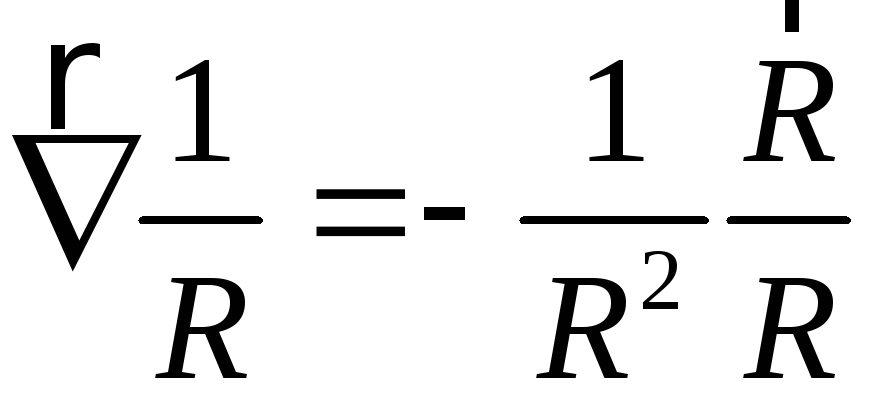 ,
знаходимо напруженість електричного
поля
,
знаходимо напруженість електричного
поля
![]() .
Вона дорівнює:
.
Вона дорівнює:
 . (4.13)
. (4.13)
2) використання теореми Остроградського-Гауса:
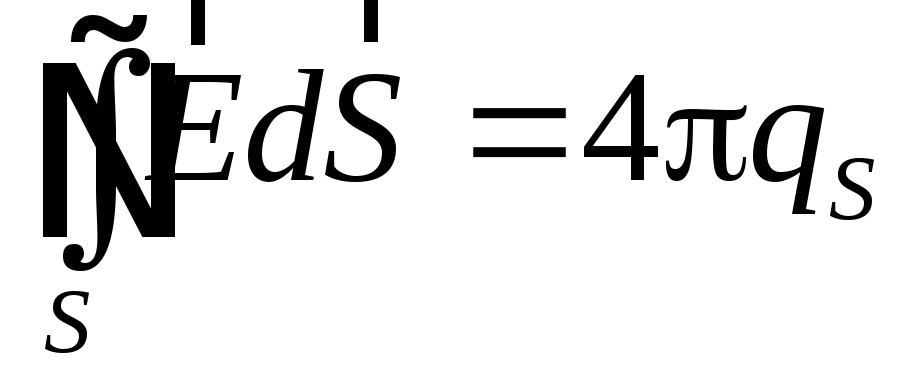 , (4.14)
, (4.14)
де
![]() -
заряд,
якій охоплюється поверхнєю
-
заряд,
якій охоплюється поверхнєю
![]() :
:
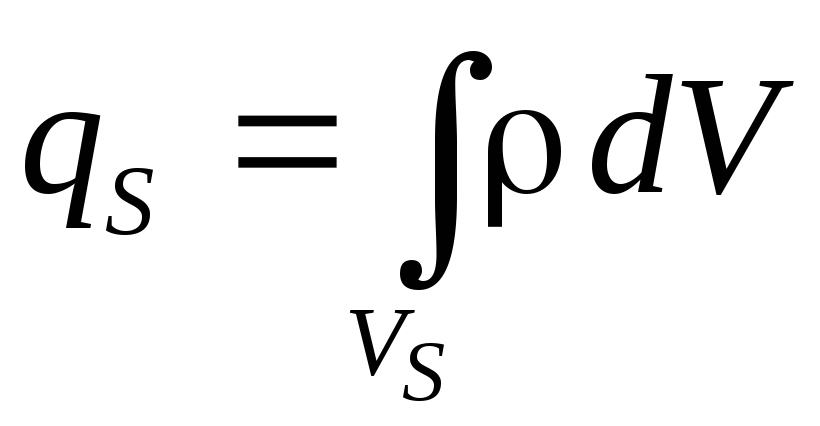 ,
,
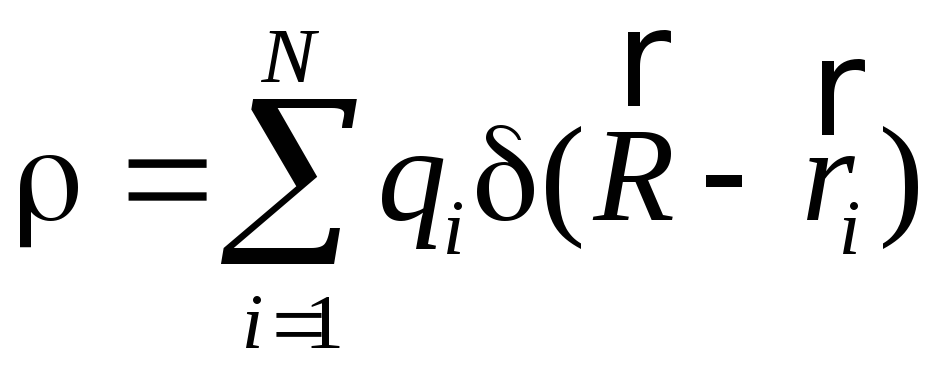 .
.
В нашій
задачі розподіл заряду має сферичну
симетрію. Тому модуль вектора напруженості
електричного поля в точці
![]() ,
може залежити тільки від модуля
радіус-вектора
,
може залежити тільки від модуля
радіус-вектора
![]() :
:
![]() .
.
Вектор
напруженості
![]() може бути направленим тільки вздовж
единого характерного напрямку - напрямку
радіус-вектора
може бути направленим тільки вздовж
единого характерного напрямку - напрямку
радіус-вектора
![]() :
:
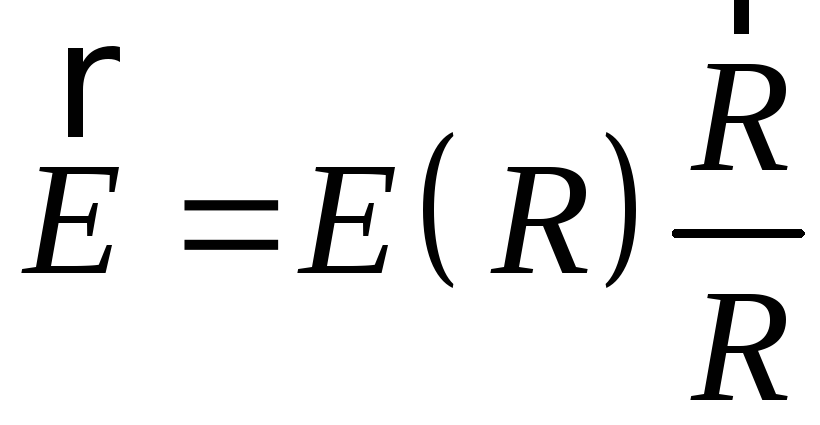 .
.
Поверхню
![]() вибираємо у вигляді сфери радіуса
вибираємо у вигляді сфери радіуса
![]() (Рис.7). Тоді
(Рис.7). Тоді
![]() .
.
Якщо
![]() ,
то
,
то
 та
та
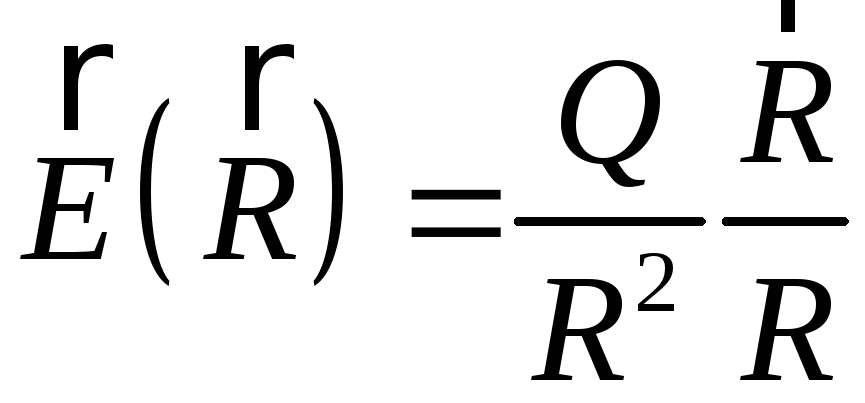 .
Якщо
.
Якщо
![]() ,
то
,
то
![]() ,
що приводить до
,
що приводить до
![]() .
.
3)
інтегрування рівняння Пуассона:
![]() .
.
В задачі, яка розглядається є дві області:
-
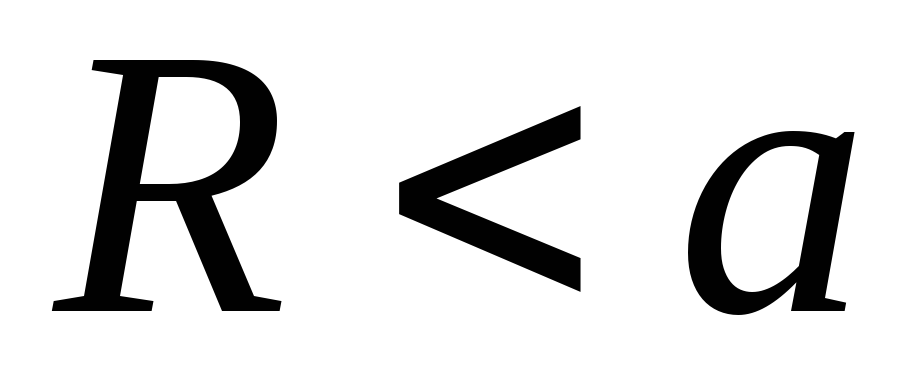 ,
(у сфері),
,
(у сфері), -
 ,
(поза сферою).
,
(поза сферою).
Границєю між ними є заряджена сфера і на ній повинні виконуватись граничні умови (4.7), які в даній задачі мають вигляд:
![]()
(4.15)
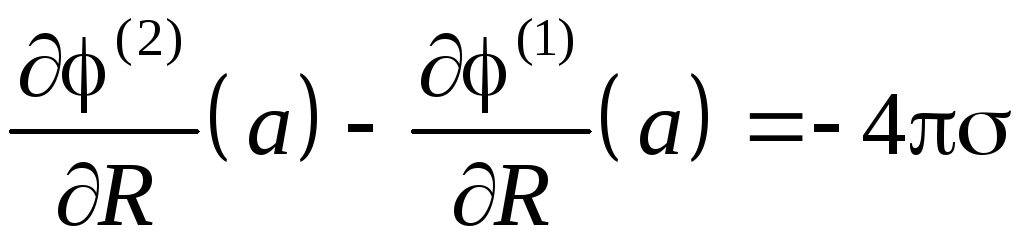
Об'ємна
густина заряду в обох цих областях
дорівнює нулеві. Тому потенціали
![]() і
і
![]() задовольняють рівнянням Лапласса:
задовольняють рівнянням Лапласса:
![]() ,
, ![]() . (4.16)
. (4.16)
Оскільки
і
![]() є функцією тільки відстані, то
є функцією тільки відстані, то
![]() ,
,
де
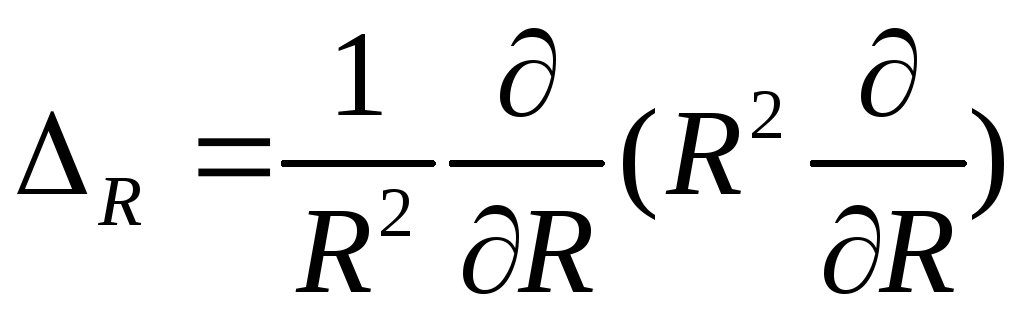 -радіальна
частина оператора Лапласа.
-радіальна
частина оператора Лапласа.
Рівнянням Лапласа (4.16) відповідають розв'язки:
 ;
;
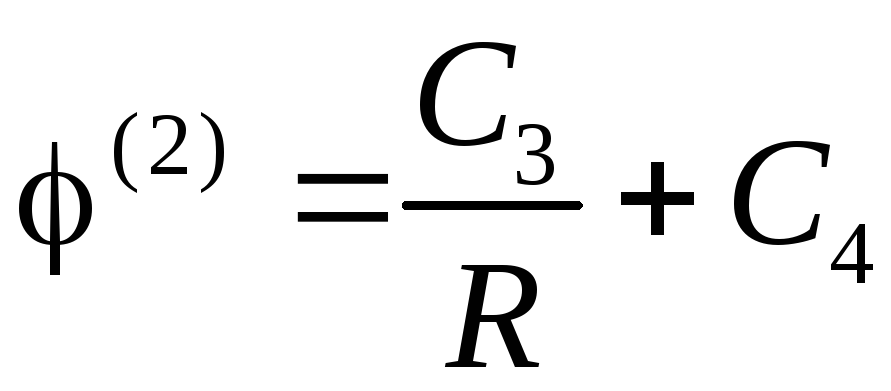 .
.
Вони
включають в себе чотири невідомі
константи, для визнячення яких ми маємо
дві граничні умови. Два додаткових
співвідношення можуть бути вибрані у
такій спосіб. Оскільки заряд розташований
в обмеженій області простору, то при
![]() значення потенціала
значення потенціала
![]() має бути прирівняним нулеві. Звідци
випливає, що
має бути прирівняним нулеві. Звідци
випливає, що
![]() .
.
При
![]() ,
,
![]() .
Оскільки в точці
.
Оскільки в точці
![]() відсутні точкові та лінійні заряди,
потенціал
відсутні точкові та лінійні заряди,
потенціал
![]() у цій точці повинен бути обмеженим. Це
можливо тільки при умові, що
у цій точці повинен бути обмеженим. Це
можливо тільки при умові, що
![]() .
.
Константи
![]() і
і
![]() знаходяться з рівнянь (див.(4.15)):
знаходяться з рівнянь (див.(4.15)):
 ;
;
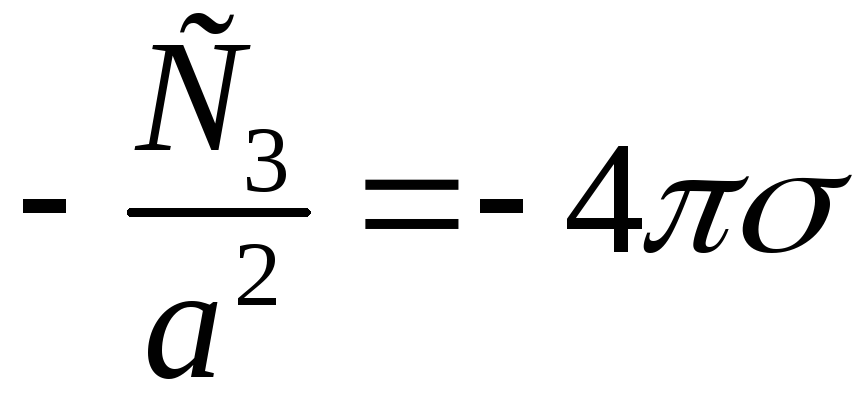 ,
,
і дорівнюють
![]() ;
;
![]() .
.
Таким чином,

4) Інтегрування рівнянь Максвела.
Рівняння Максвелла (4.2) і граничні умови (4.5) приймають таку конкретну форму:
1)
![]()
![]() ;
;![]()
2)
![]()
![]() ;
;![]()
3)
![]()
![]() ;
;
![]() ;
;![]() ;
;
Завдяки сферичної симетрії у розподілі зарядів

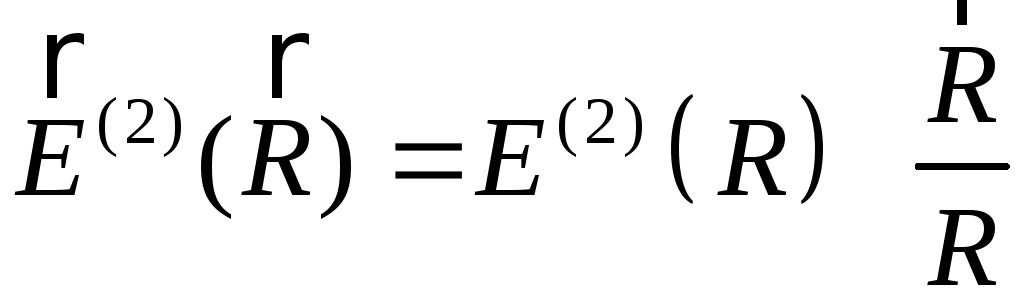 .
.
Як наслідок, рівняння для ротора напруженості в областях 1 і 2 та граничні умови для тангенціальних складових задовольняються тотожно. Рівняння для дивергенції напруженості


в областях 1 і 2 мають розв’язки:
 ,
,
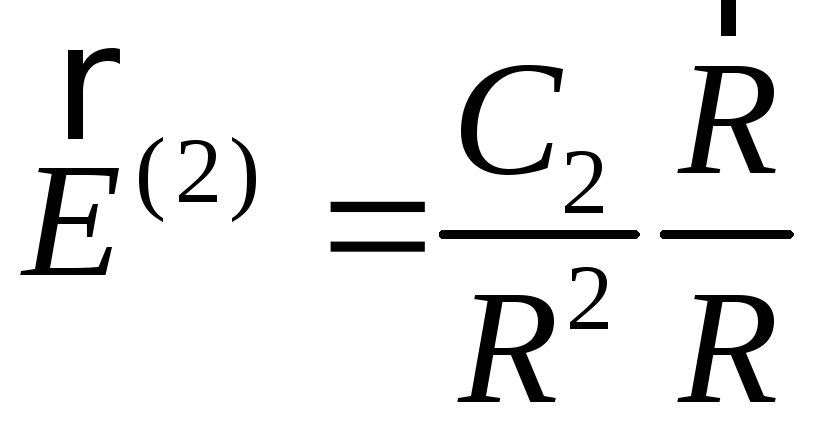 .
.
При
![]() напруженість поля
напруженість поля
![]() повинна
бути обмеженою, тому
повинна
бути обмеженою, тому
![]() і
і
![]() .
Із
граничної умови для
нормальних складових знаходимо, що,
.
Із
граничної умови для
нормальних складових знаходимо, що,
![]() ,
так що
,
так що
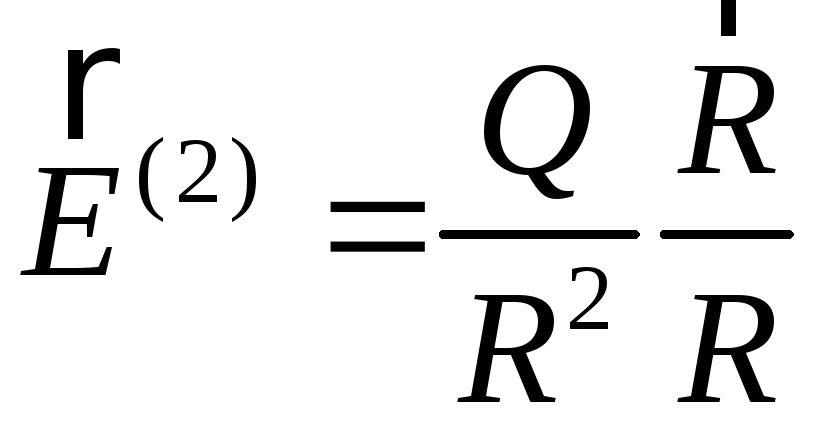 .
.
Задача.
Сфера радіуса![]() рівномірно
заряджена з поверхневою густиною
рівномірно
заряджена з поверхневою густиною
![]() .
Визначити енергію електричного поля і
тиск кулонівських сил на поверхню сфери.
Визначимо енергію
.
Визначити енергію електричного поля і
тиск кулонівських сил на поверхню сфери.
Визначимо енергію
![]() двома
способами.
двома
способами.
а) Перший
спосіб:
 ,
де
,
де
![]() визначається формулою (54).
визначається формулою (54).
Завдяки
сферичній симетрії електричного поля
інтегрування доцільно виконувати по
сферичним слоям для яких
![]() .
У такий спосіб одержуємо
.
У такий спосіб одержуємо
 . (4.17)
. (4.17)
б) Другий
спосіб:
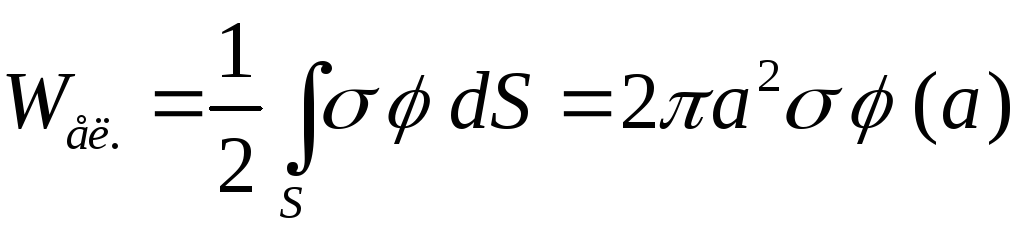 .
.
Потенціал
поля, напруженість якого змінюється
згідно (4.13), визначається виразом (4.12),
і при
![]() приймає значення
приймає значення
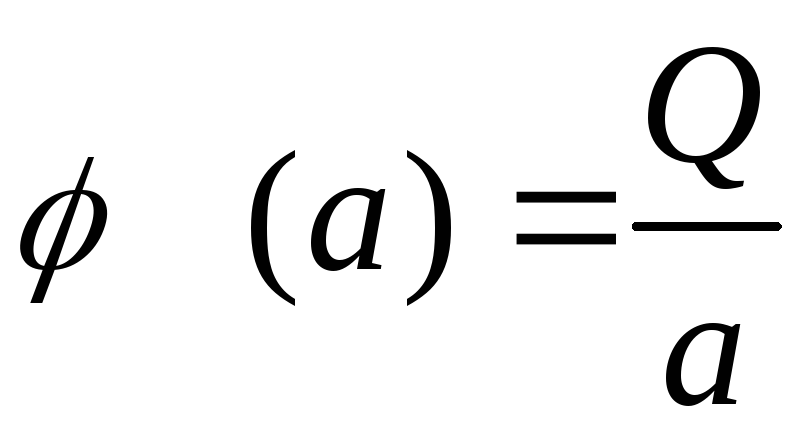 .
.
Тоді
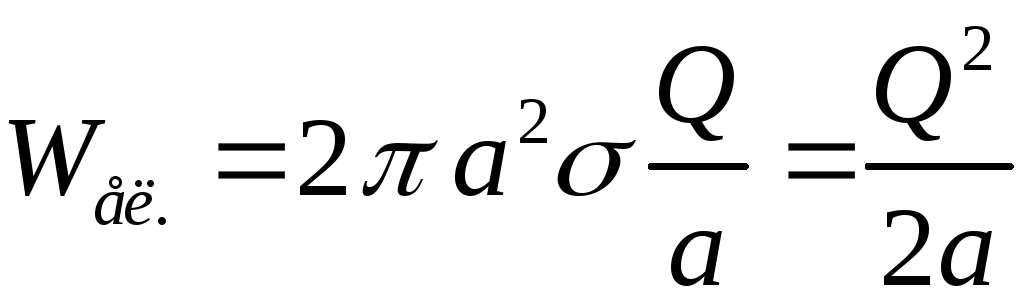 .
.
Для визначення тиску на поверхню сфери розглянемо роботу кулонівських сил при збільшенні радіуса сфери:
![]() ,
,
де
![]() -
тиск на поверхню сфери. Знак (-) враховує
зменшення енергії сфери при зростанні
її радіуса.
-
тиск на поверхню сфери. Знак (-) враховує
зменшення енергії сфери при зростанні
її радіуса.
Звідки
![]() .
.
Задачі для самостійного розв’язування.
-
Нескінченно протяжний циліндр радіуса
 заряджений:
а) по об’єму;
заряджений:
а) по об’єму;
б) по
поверхні. Заряд, який приходиться на
одиницю довжини циліндра дорівнює
![]() .
Визначити: потенціал
.
Визначити: потенціал
![]() і напруженість поля
і напруженість поля
![]() та
енергію електричного поля (на одиницю
довжини циліндра).Розглянути граничний
випадок
та
енергію електричного поля (на одиницю
довжини циліндра).Розглянути граничний
випадок
![]() (заряджена
нитка).
(заряджена
нитка).
2) В
середині рівномірно зарядженої кулі
радіуса
![]() вирізана
сферична порожнина радіуса
вирізана
сферична порожнина радіуса
![]() ,
,
![]() .
Сумарний початковий заряд кулі дорівнює
.
Сумарний початковий заряд кулі дорівнює
![]() .
Визначити характеристики електричного
поля (
.
Визначити характеристики електричного
поля (![]() і
і
![]() )
та його енергію.
)
та його енергію.
3) Площина заряджена з густиною
![]() ,
,
де
![]() ,
,![]() ,
,![]() - сталі. Знайдіть потенціал
- сталі. Знайдіть потенціал
![]() цієї системи зарядів поблизу площини.
цієї системи зарядів поблизу площини.
4) Об'єм
між двома концентричними сферами з
радіусами
![]() і
і
![]() заряджений з об’ємною густиною:
заряджений з об’ємною густиною:
а)
![]() ,
б)
,
б)
 ,
в)
,
в)
![]() .
.
Знайти
параметри поля (![]() ,
,
![]() ),
повний заряд
),
повний заряд
![]() і енергію
і енергію
![]() електростатичного
поля.
електростатичного
поля.
5) На
відстані
![]() від зарядженої нитки знаходиться
рівномірно заряджена сфера радіуса
від зарядженої нитки знаходиться
рівномірно заряджена сфера радіуса
![]() .
Густина заряду на сфері
.
Густина заряду на сфері
![]() та заряд одиниці довжини нитки
та заряд одиниці довжини нитки
![]() сталі. Знайти параметри поля (
сталі. Знайти параметри поля (![]() ,
,
![]() )
і силу взаємодії між ниткою та сферою.
)
і силу взаємодії між ниткою та сферою.
6) Яким повинен бути розподіл зарядів, щоб потенціал, який вони утворюють мав вигляд:

7) Заряд електрона розподілений в атомі водню, який знаходиться в нормальному стані, з густиною
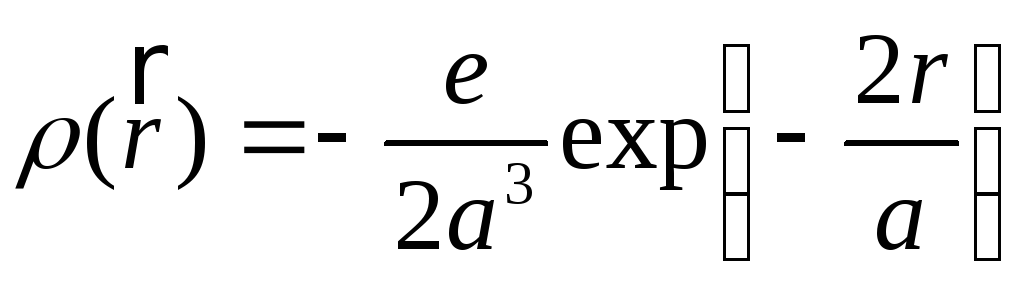 ,
,
де
![]() - боровський радіус атома,
- боровський радіус атома,
![]() -заряд
електрона.
-заряд
електрона.
Знайти
потенціал
![]() і напруженість поля
і напруженість поля
![]() в атомі, вважаючи, що протон знаходиться
на початку координат.
в атомі, вважаючи, що протон знаходиться
на початку координат.
8)
Потенціал електричного поля дається
формулою
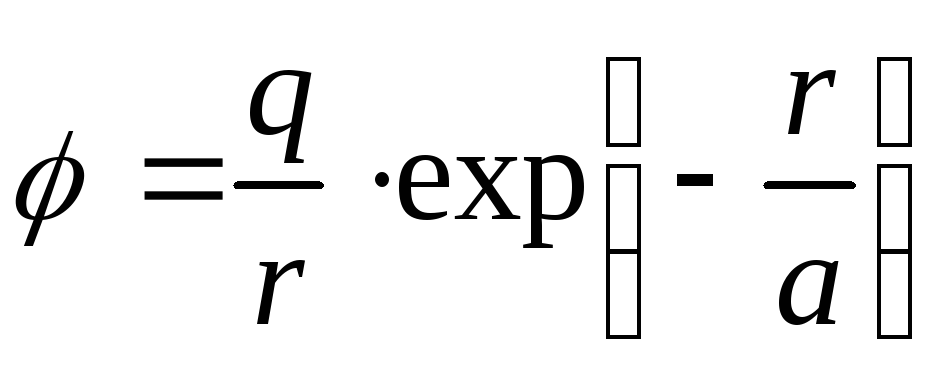 (потенціал Юкави). Знайти розподіл заряду
(потенціал Юкави). Знайти розподіл заряду
![]() .
.
4.3 Мультипольний розклад в електростатиці
Якщо відстань до точки, в якій потрібно визначити електричне поле значно перебільшує розмір системи, яка утворює поле, можна використовувати мультипольний розклад:
 , (4.18)
, (4.18)
де
![]() -повний
заряд системи (скаляр);
-повний
заряд системи (скаляр);
![]() -дипольний
момент системи (вектор);
-дипольний
момент системи (вектор);
![]() -квадрупольний
момент системи (симетричний, безслідовий
тензор другого рангу),
-квадрупольний
момент системи (симетричний, безслідовий
тензор другого рангу),
![]() -декартові
компоненти радіуса-вектора
-декартові
компоненти радіуса-вектора
![]() .
.
Для системи точкових зарядів:
![]() ;
;
 , (4.19)
, (4.19)
де
![]() -декартові
координати радіуса-вектора
-декартові
координати радіуса-вектора
![]()
![]() -го
заряду.
-го
заряду.
Для просторового розподілу заряду:
 ;
;
 , (4.20)
, (4.20)
де
![]() -
декартові координати радіуса-вектора
-
декартові координати радіуса-вектора
![]() .
.
Задача.
Знайти потенціал поля, яке утворюється
трьома точковими зарядами:
![]() ;
;
![]() ;
;
![]() ,
розташованими у точках
,
розташованими у точках
![]() ;
;
![]() ;
;
![]() .
.
Повний заряд системи:
![]() .
.
Компоненти вектора дипольного момента:
![]() ;
;
![]() ;
;
![]() .
.
Очевидно, що всі недіагональні компоненти тензора квадрупольного момента дорівнюють нулеві. Напроти:
![]() ;
;
![]() .
.
Оскільки тензор безслідовий, то
![]()
Таким чином, маємо:

Задачі.
1) В
попередній задачі визначити напруженість
поля
![]() .
.
2) Довести,
що при
![]() ,
,
![]() не залежить від вибору початку координат.
не залежить від вибору початку координат.
3) Знайти потенціал поля, яке утворюється чотирма точковими зарядами, розташованими у вершинах квадрата. Значення зарядів:
![]() ;
; ![]() .
.
4)
Використовуючи мультипольний розклад
знайти потенціал поля, яке утворюється
відрізком нескінчено тонкої нитки,
одиниця довжини якої має заряд
![]() .
Довжина відрізка
.
Довжина відрізка
![]() .
.
5)
Використовуючи мультипольний розклад
знайти потенціал поля, яке утворюється
нескінченно тонким кільцем, радіуса
![]() .
.
6) Сфера
радіуса
![]() заряджена за законом:
заряджена за законом:
а)
![]() ;
;
![]() б)
б)
![]() .
.
Знайти мультипольні моменти такого розподілу зарядів.
Знайти
характеристики поля (![]() ,
,![]() ,
,![]() ).
).
7) Знайти
силу
![]() та обертальний момент
та обертальний момент
![]() ,
які діють на електричний диполь
,
які діють на електричний диполь
![]() :
:
а) у
зовнішньому полі з напруженостю
![]() ;
;
б) у полі точкового заряду.
8) Диполь
![]() закріплений на початку координат. Другий
диполь
закріплений на початку координат. Другий
диполь
![]() знаходиться у точці
знаходиться у точці
![]() і може вільно обертатися. Визначити:
і може вільно обертатися. Визначити:
а) енергію взаємодії диполів;
б) рівноважну орієнтацію.
9)
Визначити квадрупольний момент еліпсоїда,
який рівноважно заряджений з об’ємною
густиною
![]() .
.
