Для студентов / (1)Векторы / 1Вектори

Вектори

За означенням, вектор є направлений відрізок прямої, який починається а точці і закінчується в точці :

Таке означення не є пов’язаним з тією чи іншою системою координат і тому можна твердити, що вектор є інваріантним об’єктом.

Як правило, вектори позначаються однією літерою: і т.п. Вектор характеризується направленням, величиною або модулем, який позначається як або і, якщо це важливо, то і точкою прикладення (точкою, з якої вектор виходить).

Добутком вектора на число є вектор , який має той же напрямок, що і вектор , а модуль якого дорівнює .

Вектор , модуль якого дорівнює одиниці, прийнято називати одиничним вектором. равен единице, принято называть единичным вектором. Довільний вектор , очевидно, може бути представлений у вигляді:

, (1)

де є одиничний вектор, направлений вздовж .

Сумою двох векторів і є вектор , пов'язаний з вихідними векторами правилом паралелограма:

Природнім шляхом означення суми узагальнюється і для сукупності більшого числа векторів: . Спочатку за правилом паралелограма будується вектор , потім таким же чином будується вектор і т.д.

Вектор , який в сумі з дає вектор нульової довжини, називають зворотнім вектором і позначають як : . Введення зворотного вектора означає, що різниця векторів і не є незалежною операцією, а повинна розглядатись як сума вектора і вектора , зворотного до , тобто .

Добуток скалярного множника на суму векторів задовольняє умові асоціативності:

. (2)

Користуючись правилом паралелограма, довільний вектор у вимірному просторі можна розкласти на складові, направлені вздовж взаємно-непаралельних одиничних векторів ,…,, які виходять з однієї точки:

Таким чином, довільний вектор може бути записаний у вигляді:

. (3)

Враховується, що по двох однакових індексах, що повторюються, виконується сумування: (у випадку трьох або більшого числа однакових індексів сумування не передбачається). Числа ,…, называють компонентами вектора в базисі . Зокрема, вектор , який з’єднує точку , в якій перетинаються всі базисні вектори, з довільною точкою в просторі, називають радіус-вектором цієї точки. Як і для вектора , має місце представлення:

, (4)

де - координати радіус-вектора.

Скалярним добутком векторів і називають число , яке утворюється наступним чином:

. (5)

У згоді з означенням, скалярний добуток векторів не змінюється при перестановці векторів і місцями, тобто задовольняє умові комутативності:

=. (6)

Скалярний добуток на суму векторів узгоджується з вимогою асоціативності:

. (7)

Якщо , де не обов’язково дорівнює , то користуючись правилами асоціативності і комутативності скалярних добутків, знаходимо:

=. (8)

Якщо , ,…, , і , ,…, , то з (9) випливає:

=. (10)

Важливим окремим випадком є той, коли всі одиничні вектори є взаємно-ортогональними:

,

де символ Кронекера:

. (11)

В цьому випадку з (10) випливає, що

. (12)

Квадрат вектора у згоді з (12) задовольняє теоремі Піфагора:

, (13)

тобто для модуля вектора , очевидно, можна написати .

Порівнюючи (5) і (12), знаходимо наступний вираз для косинуса кута між векторами і :

. (14)

Векторний добуток векторів і , який позначається як , за означенням, дорівнює: , де

,

а одиничний орт є ортогональним площині, яка спирається на вектори і , і направленим так, щоб співпадати з напрямком руху буравчика, коли його ручку повертають від напрямку до .

Напрямок векторного добутка векторів і можна визначати і дещо іншим способом. З кінця вектора поворот від вектора до повинен відбуватися проти напрямку руху часової стрілки.

З означення випливає, що векторний добуток двох паралельних векторів, зокрема двох однакових векторів, дорівнює нулю.

Завдяки такому означенню орта , векторний добуток векторів і є анти- комутативним:

. (15)

Важливу формулу для векторного добутку можна отримати у тривимірному просторі, коли орти є взаємно-ортогональними. Нехай орти зорієнтовані наступним чином:

Тоді, у згоді з означенням векторного добутку можна написати:

, , . (16)

Тут порядок розташування індексів відповідає їх циклічним (парним) перестановкам, починаючи з . Іншим ненульовим векторним добуткам ортів:

, , . (17)

відповідають непарні перестановки тих самих індексів. Дійсно, відповідні комбінації можна отримати, виконуючи наступні перестановки сусідніх пар чисел:

, ,

,

Хоча векторний добуток є не комутативним, але він залишається асоціативним. Враховуючи цю властивість, можна написати:

.

Векторний добуток двох ортів в залежності від значень індексів співпадає з однією з можливостей (16) чи (17), або зводиться до комбінації , що дорівнює нулю внаслідок паралельності множників. Таким чином знаходимо:

. (18)

Комбінація з правого боку рівняння (18), фактично, співпадає з розкладом детермінанта третього порядку за елементами його першої строки , так що

. (19)

Можна також впевнитись, що кожний з доданків в правій частині (18) утворюється за правилом:

, (20)

де є, так званий, повністю антисиметричний тензор третього порядку, який задається співвідношенням

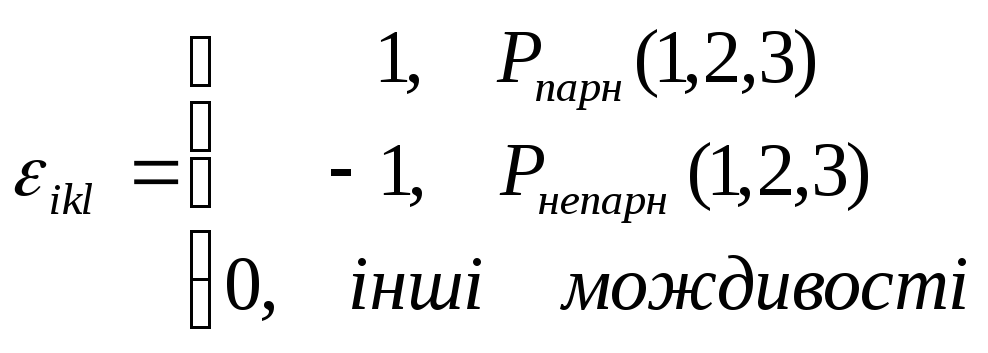, (21)

де - оператор парного числа перестановок індексів , - оператор непарного числа перестановок індексів . «Інші можливості» включають комбінації індексів, серед яких два чи більше дорівнюють одне одному.

У згоді з (21):

,

,

.

Отримані результати дають можливість перейти до розгляду найбільш вживаних скалярних і векторних добутків трьох і чотирьох різних векторів.

Розрахунок , ,

Розглянемо властивості скаляра в тривимірному просторі з ортогональною трійкою базисних векторів .

Утворимо скалярний добуток , використовуючи для векторного добутку формулу (18). Неважко бачити, що

=, (22)

або

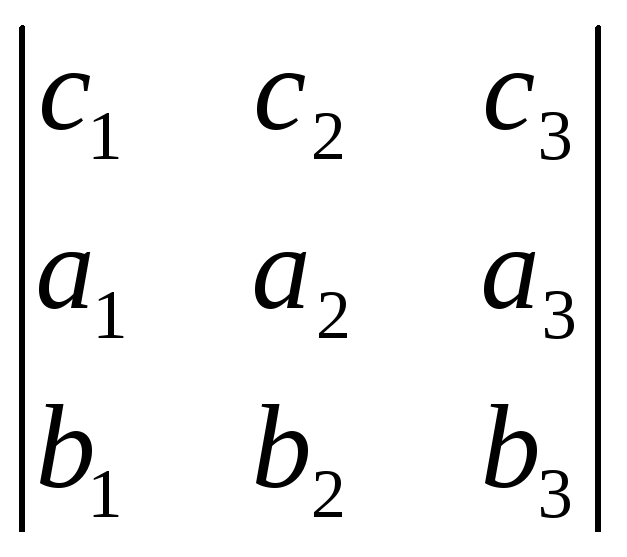=. (23)

Якщо ми скористаємось формулою (20), то знайдемо:

. (24)

Виконаємо одну з циклічних перестановок індексів , а саме . Оскільки , то

.

У такий самий спосіб знаходимо, що змішаний скалярно-векторний добуток є інваріантним відносно всіх циклічних перестановок векторів, тобто

. (25)

Якщо перестановка векторів є ациклічною, то знак відповідного змішаного добутку є протилежним знаку .

Перейдемо тепер до спрощення подвійного змішаного добутку . Перш за все відмітимо, що вектор лежить в площині, утвореній векторами і . Дійсно, вектор є перпендикулярним до площини, яка задається векторами і . Але вектор, перпендикулярний до , повинен бути паралельним площині, утвореній векторами і .

Внаслідок цього повинен бути лінійною комбінацією векторів і :

.

Для знаходження коефіцієнтів і помножимо ліву і праву частини цього рівняння на вектор . Оскільки , то

.

Це рівняння має місце при довільних векторах , і , з чого випливає, що

, ,

де - довільний чисельний множник, який не залежить від вихідних векторів. Таким чином,

. (26)

Для знаходження візьмемо , і . Прямим розрахунком знаходимо, що . В той же час, з (26) випливає, що , тобто .

Таким чином,

=. (27)

Для знаходження позначимо . Виконаємо ланцюжок перетворень:

.

Ключовою ланкою тут є циклічна перестановка: . Далі, розкриваємо подвійний векторний добуток: і остаточно, отримуємо

. (28)

Формула (29) приводить до корисного співвідношення між компонентами повністю антисиметричного тензора. Дійсно, з (20) випливає, що і , тобто . Для того, щоб цей результат узгоджувався з (28), потрібно покласти

. (29)

З (28) випливає, що

. (30)

Використовуючи важливе співвідношення для компонентів повністю антисиметричного тензора (див. ())

= ---+-, (31)

можна суттєво спростити також скалярну комбінацію з шести векторів: . Дійсно, спираючись на вище встановлені співвідношення і та формулу (31), отримуємо:

(32)

Аналогом (30) є формула:

. (33)

Найпростіші застосування скалярного і векторного добутків

Проекція вектора на напрямок, який задається вектором , пов’язана зі скалярним добутком формулою:

, (34)

де - одиничний вектор, паралельний вектору .

Довільний вектор завжди можна представити у вигляді:

, (35)

де і є складові вектора , направлені вздовж і перпендикулярно якомусь другому

вектору . Оскільки , де , то можна надати вигляд:

. (36)

Перпендикулярна або поперечна складова вектора знаходиться як різниця між і :

. (37)

Площа трикутника, побудованого на векторах і як на сторонах, дорівнює:

. (38)

Рівняння площини, яке в декартових координатах має вигляд

,

переходить у

(39)

де - радіус-вектор точки, яка належить площині, а - вектор, проекції якого на вісі координат дорівнюють: . Довільний вектор , який лежить у площині, очевидно, задовольняє рівнянню: