Вектори в довільних криволінійних системах координат

Розглянемо вимірну криволінійну систему координат . Система координат буде називатись криволінійною, якщо її координатні лінії, тобто лінії вздовж яких змінюється тільки одна з координат, в загальному випадку не є прямими.

Величини

, (1)

де е вектор зміщення точки при зміні тільки його ї координати на величину , називають коваріантними базисними векторами. З означення випливає, що базисні вектори в загальному випадку не є нормованими на одиницю і не утворюють сукупність взаємно-ортогональних векторів.

Спираючись на правило паралелограма довільний вектор зміщення точки можна розкласти в ряд по базисним векторам:

. (2)

Так само можна розкласти і довільний вектор :

. (3)

Компоненти прийнято називати контраваріантними компонентами вектора .

За означенням, сукупність скалярних добутків базисних векторів:

(4)

називають коваріантними компонентами метричного тензора. Він є симетричним відносно перестановок індексів:

.

Контраваріантні компоненти метричного тензора утворюються згідно означенню:

, (5)

де - обернена матриця, . В явному вигляді

,

де є алгебраїчним доповненням до елемента матриці , а - детермінант матриці. Згідно правилам побудови:

, (6)

де - символ Кронекера. Таким самим чином можна впевнитись, що

. (7)

За означенням, контраваріантні базисні вектори дорівнюють:

. (8)

Найважливішою властивістю сукупностей коваріантних і контраваріантних базисних векторів є їх взаємна ортогональність:

, (9)

що є безпосереднім наслідком (6). Дійсно, .

Коваріантні компоненти вектора утворюються за правилом:

, (10)

завдяки якому вектор може бути представленим наступним симетричним чином:

. (11)

Підкреслимо, що в криволінійних координатах опис довільного вектора за допомогою його контраваріантних і коваріантних компонентів є абсолютно рівнозначним. Виключення складає тільки диференціал радіус-вектора точки: він задається тільки контраваріантними компонентами: .

Введення контраваріантних і коваріантних компонентів вектора, дозволяє скалярний добуток векторів і представити в одному із чотирьох виглядів:

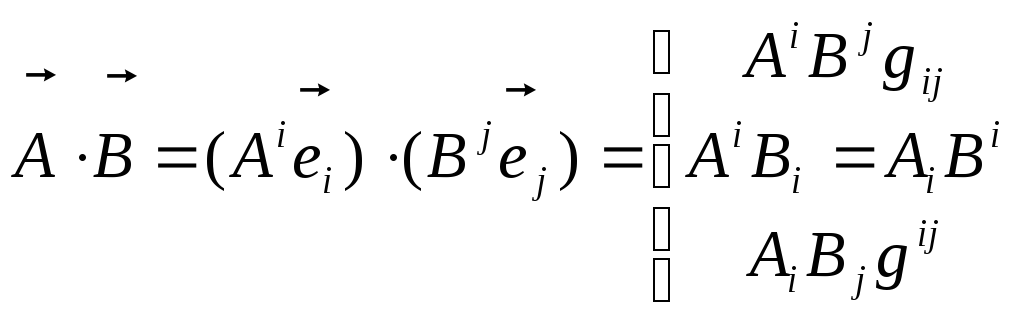. (12)

Як бачимо, найбільш просту і зручну форму має скалярний добуток у змішаному представленні, коли компоненти одного з векторів є контраваріантними, а другого – коваріантними.

Розглянемо тепер закони перетворення контраваріантних і коваріантних

компонентів вектора при переході від одної криволінійної системи координат до другої. Почнемо з його контраваріантних компонентів.

Оскільки вектор є інваріантним об’єктом, то ми можемо написати

,

де штрих вказує на приналежність величини до другої системи координат. Утворюючи скалярний добуток вектора і базисного вектора , знаходимо:

.

Таке ж саме співвідношення має місце між компонентами приросту радіус-вектора :

.

Якщо серед компонентів відмінною від нуля буде тільки компонента , то скалярний добуток , фактично, буде зводитись до похідної:

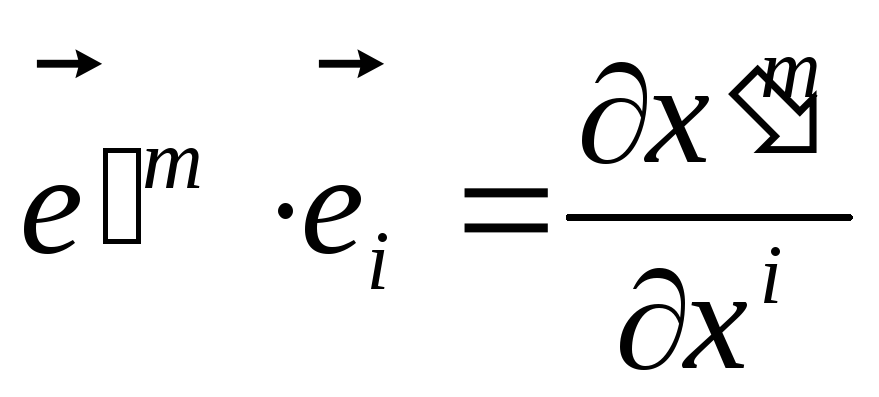. (13)

Таким чином

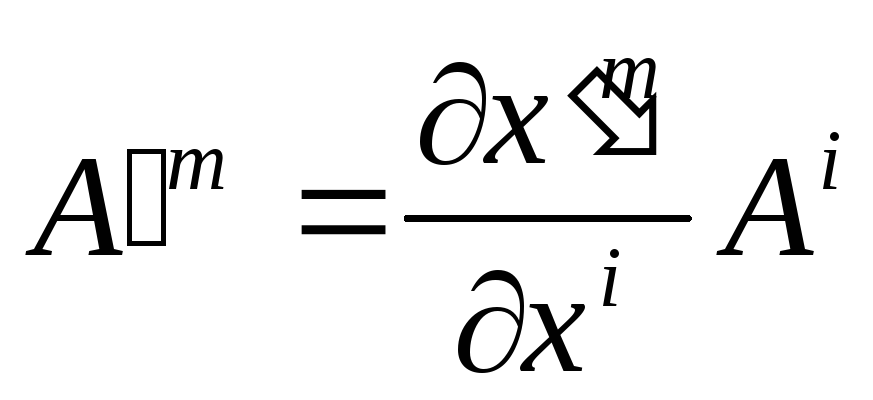. (14)

Потрібно зазначити, що у такий самий спосіб перетворюються компоненти диференціала зміщення точки:

;

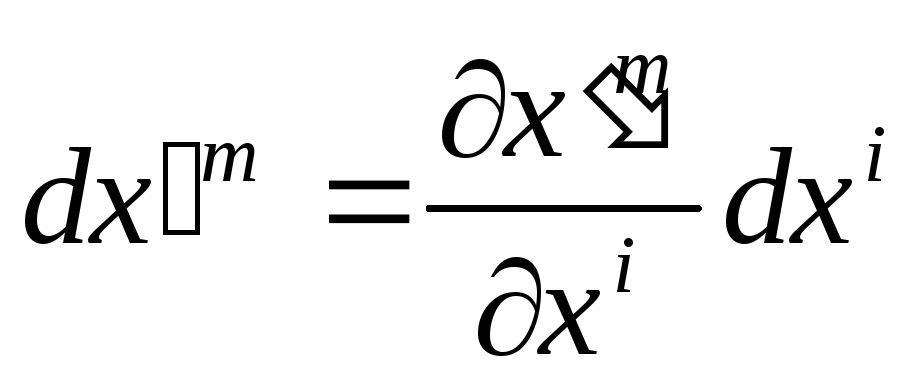Побудуємо тепер закон перетворення коваріантних компонент вектора , для чого скористаємось змішаним представленням скалярного добутку :

.

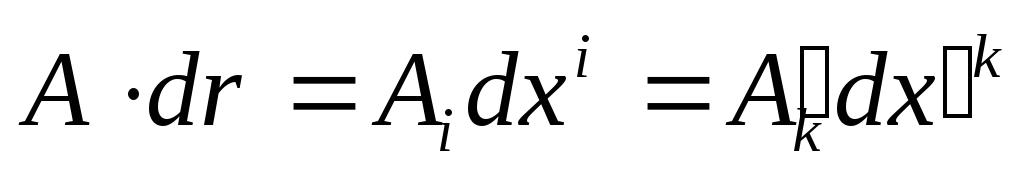Тут враховано, що описується тільки контраваріантними компонентами. Розглядаючи випадок, коли тільки , отримуємо наступний закон перетворення коваріантних компонентів вектора :

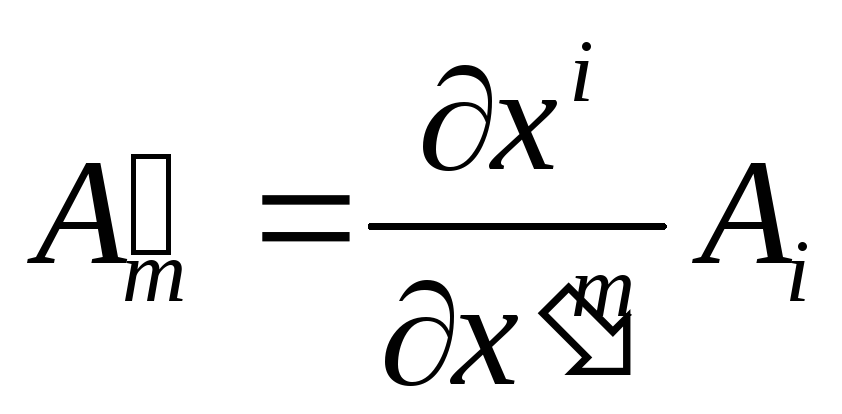. (15)

Закони перетворення базисних векторів будуються цілком аналогічно. Так, виходячи з представлення , безпосередньо знаходимо:

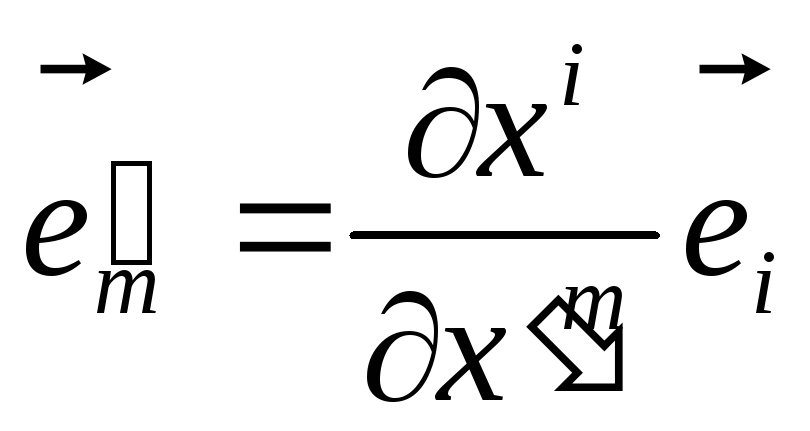. (16)

Закон перетворення контраваріантних базисних векторів має вигляд:

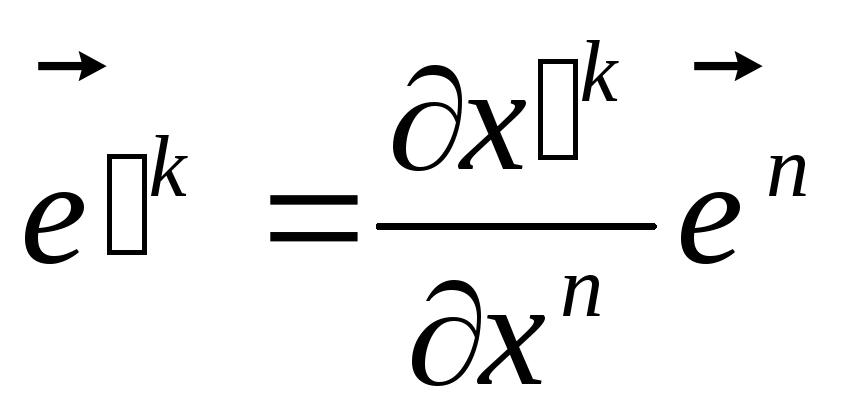. (17)

В цьому можна переконатись, утворюючи скалярний добуток . Переходячи в ньому за формулами (16) і (17) до не штрихованих базисних векторів, отримуємо:

.

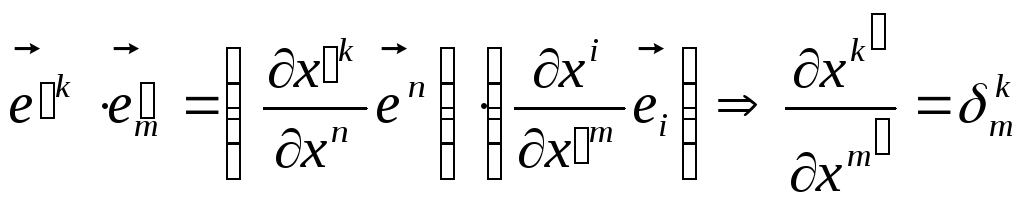Це означає, що (16) і (17) є не протирічними законами перетворення базисних векторів.