Для студентов / (1)Векторы / 4Перетворення компонентів векторів при поворотах

Перетворення компонентів векторів при поворотах системи координат

В загальному випадку поворот ДСК є комбінацією трьох елементарних поворотів, які описуються кутами Ейлера. Як перший крок, розглянемо поворот ДСК на кут навколо вісі вихідної системи координат.

Компоненти радіус-вектора перетворюються стандартним чином:

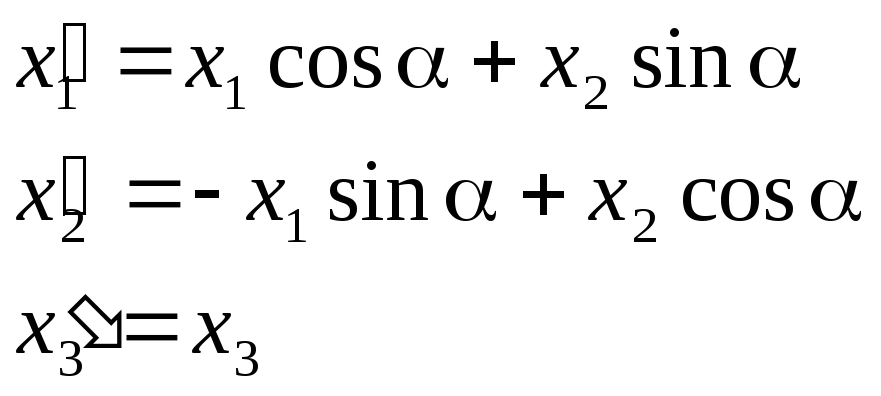. (1)

Скориставшись формулами Ейлера:

,

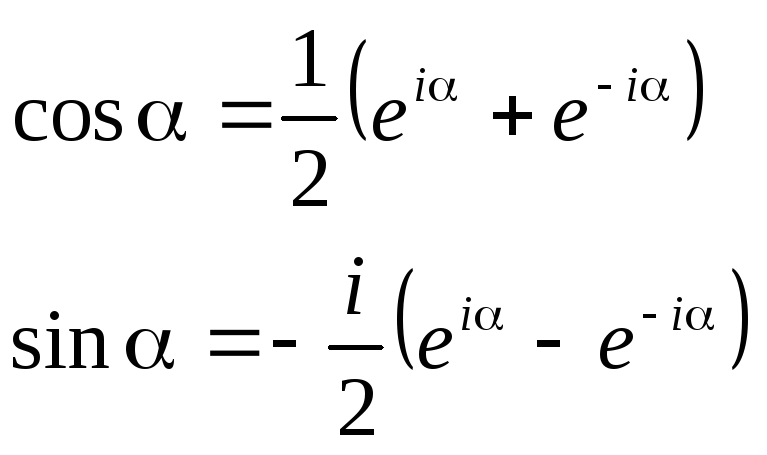перетворення (1) можна переписати у вигляді:

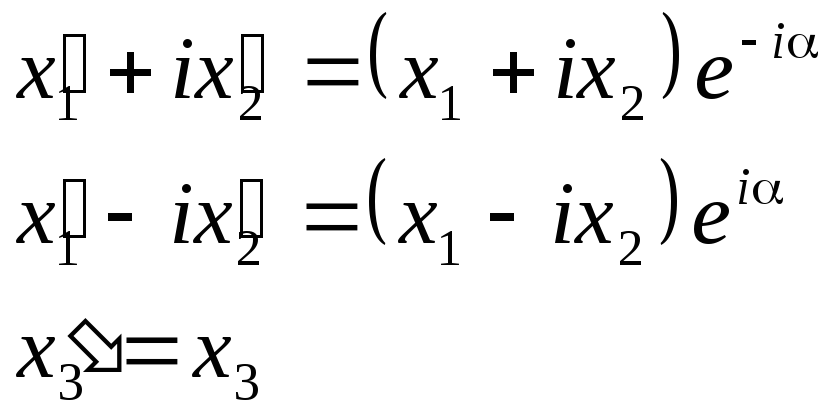. (2)

За означенням, комбінації:

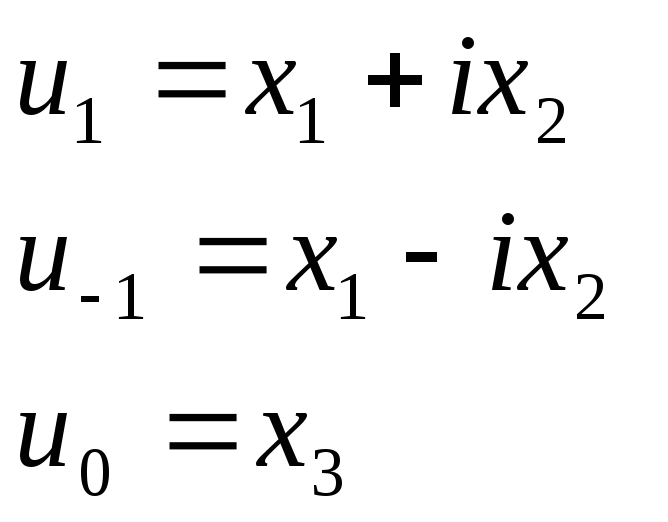(3)

прийнято називати циркулярними компонентами радіус-вектора точки. Обернене перетворення компонентів радіус-вектора описується формулами:

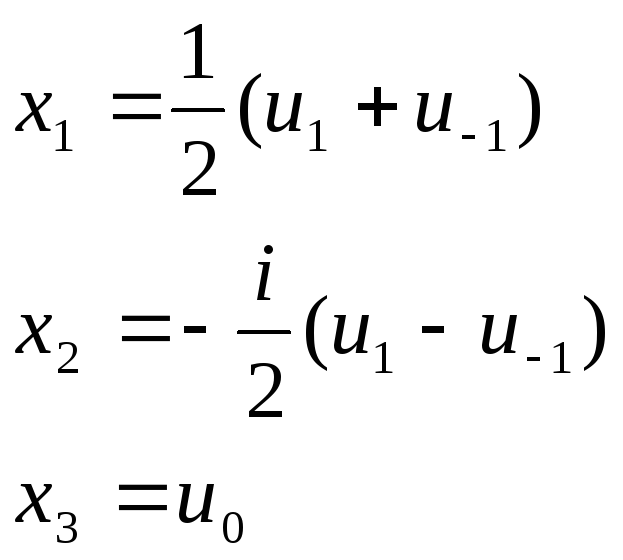(4)

Окрім циркулярних компонентів радіус-вектора можна ввести також циркулярні базисні вектори. Для цього замість компонентів в представлені радіус-вектора підставимо його циркулярні компоненти. У такий спосіб отримуємо:

, (5)

де

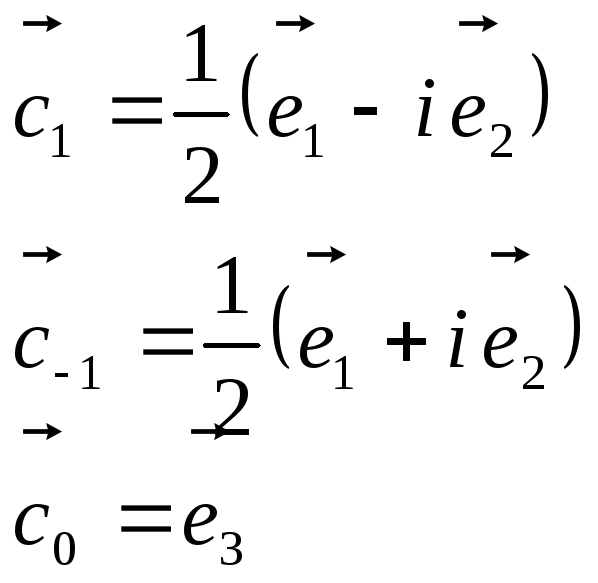(6)

є циркулярні базисні вектори. На відміну від ортів вихідної ДСК базисні вектори не є ні ортогональними, ні нормованими. Завдяки уявній одиниці, взагалі, .

Перетворення можна подати також в матричній формі:

, (7)

де

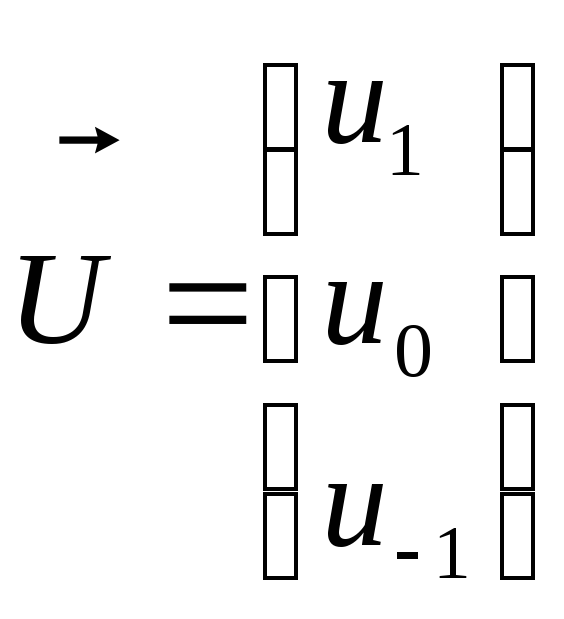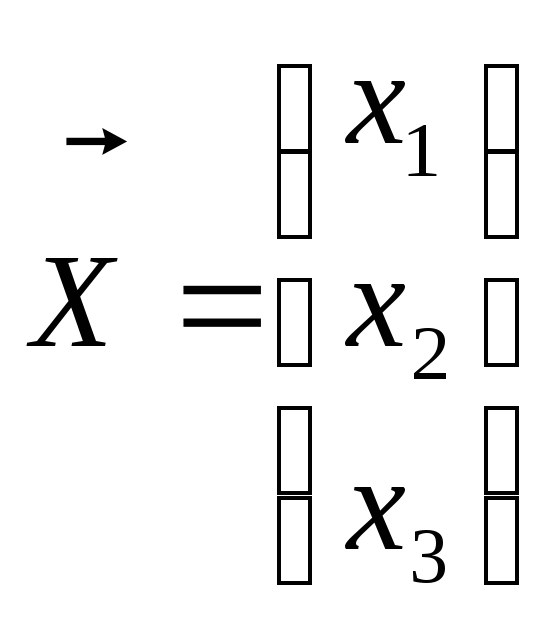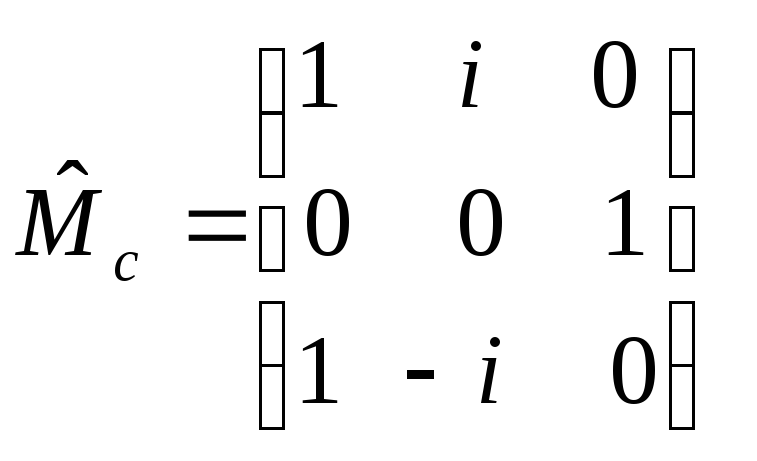, , . (8)

Оберненому перетворенню

(9)

Відповідає матриця:

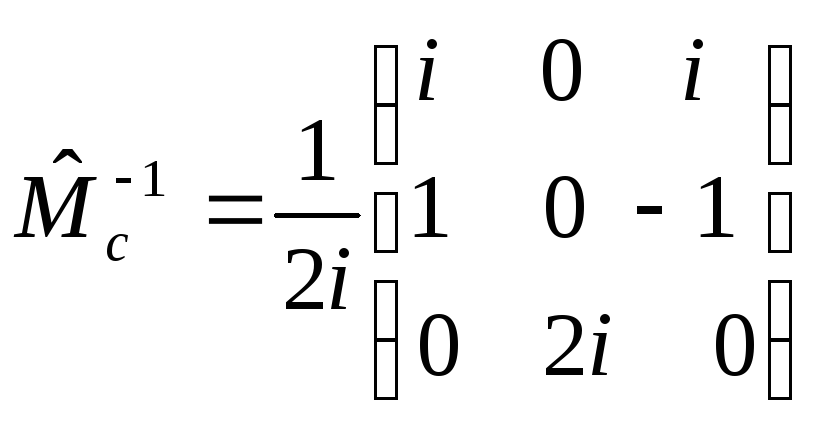. (10)

Довільний поворот ДСК можна описати сукупністю трьох послідовних елементарних поворотів:

1) навколо осі на кут ; 2) навколо осі на кут ; 3) навколо осі на кут .

Тут - вісь нової ДСК, утвореної в результаті другого поворота. Кути є відомими кутами Ейлера.

Компоненти радіус-вектора в ДСК, утвореній внаслідок першого елементарного поворота на кут , визначаються рівнянням:

,

де

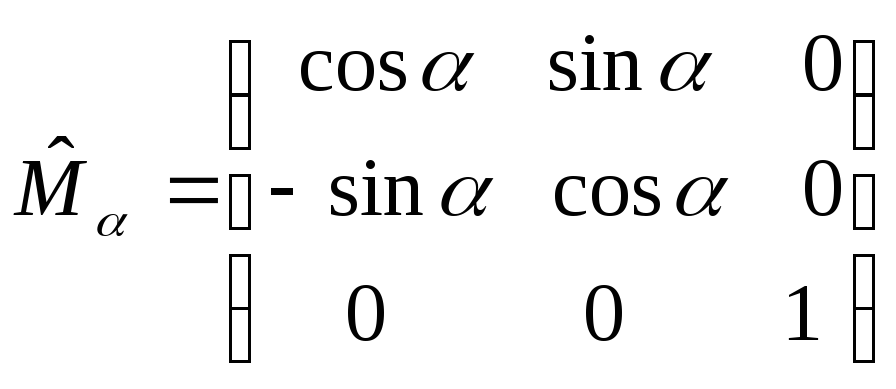. (11)

Після другого поворота компоненти радіус-вектора в новій ДСК є пов’язаними з аналогічним рівнянням:

, (12)

де

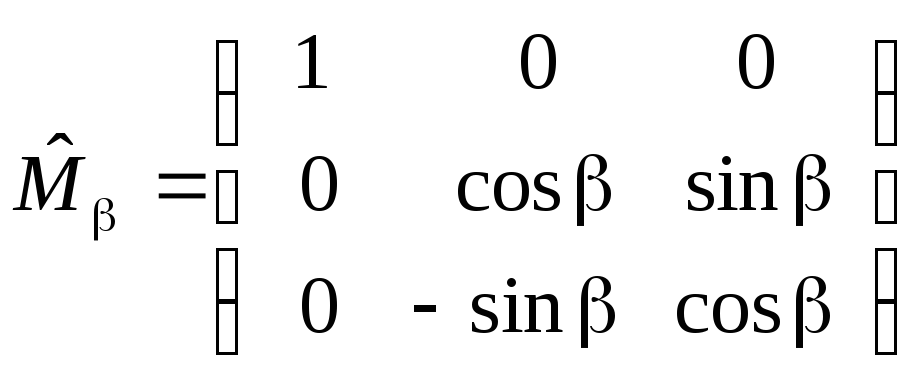. (13)

Третій поворот на кут виконується навколо осі . Йому відповідає наступне перетворення компонентів радіус-вектора:

, (14)

де

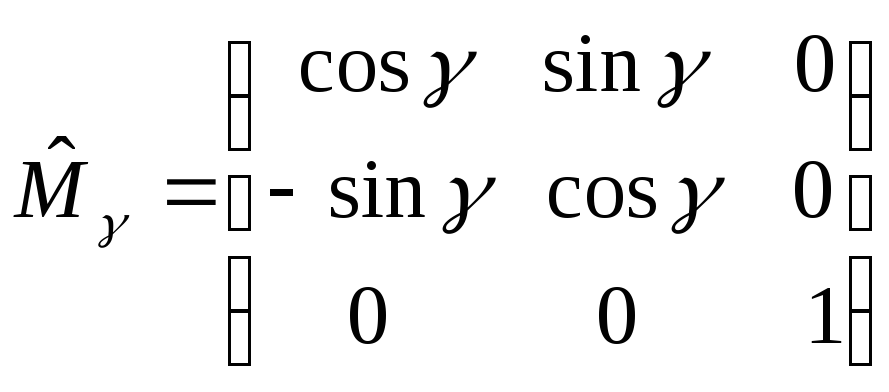. (15)

Остаточно, результатом трьох послідовних перетворень компонентів радіус-вектора буде рівняння:

, (16)

де матриця дорівнює:

Використовуючи формули (7), (9) і (16), неважко зрозуміти, що перехід від вихідних циркулярних компонентів до кінцевих виконується за допомогою перетворення:

. (17)

Надаючи формулі (17) вигляд

, (18)

ми приходимо до означення функцій Вігнера першого порядку. Безпосереднім розрахунком за формулою (17) можна впевнитись, що

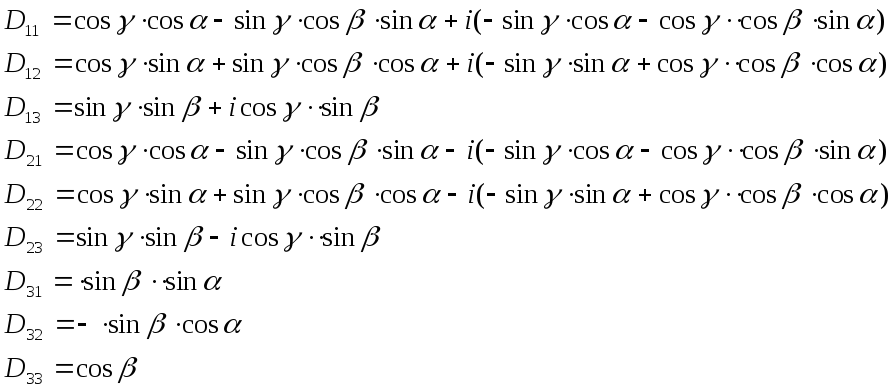
Зазначимо, що формули Вігнера знаходять широке застосування в теорії обертального руху, особливо в квантовій механіці.

Циркулярні компоненти довільного вектора утворюються цілком аналогічно (4):

=, (19)

де - його декартові компоненти. Зв'язок між декартовими і циркулярними компонентами вектора описується формулами, які є структурно тотожні (16) і (18):

ДСК: , , (20)

і

ЦСК: , . (21)

З умови інваріантності вектора відносно довільних поворотів систем координат:

,

можна знайти також матрицю , яка описує перетворення циркулярних базисних векторів:

. (22)

Неважко бачити, що компоненти матриці задовольняють рівнянню:

. (23)

Зокрема, якщо поворотам навколо осі відповідає (див. (2))

,

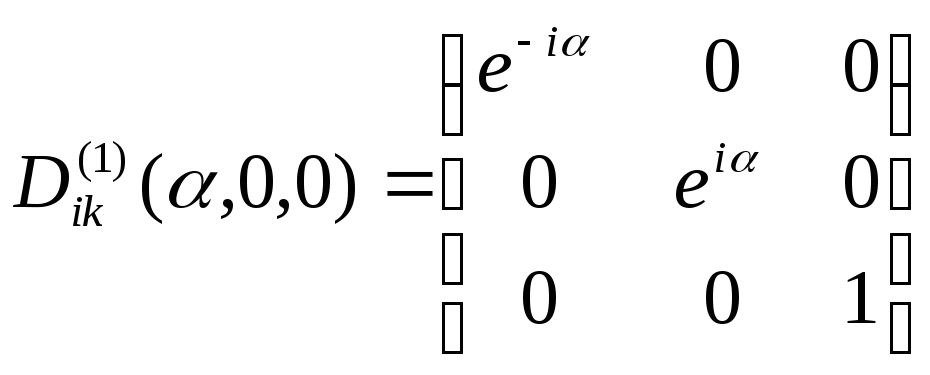то компоненти матриці дорівнюють:

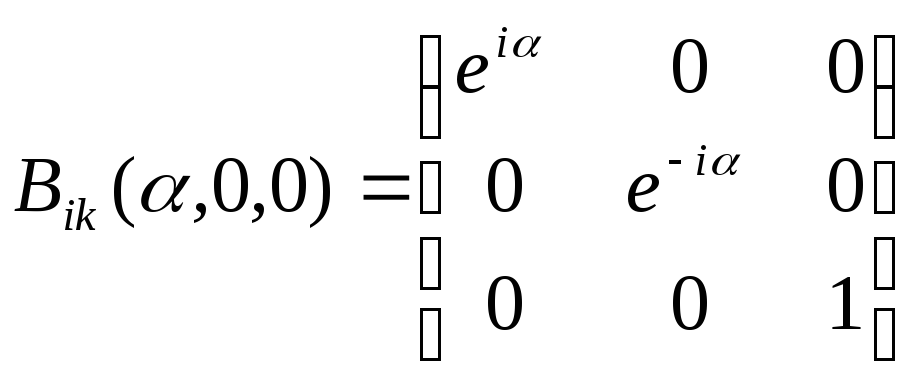. (24)