Для студентов / Лекции / (2)ВЕД / (10)Запізнюючі потенціали

10. Рішення неоднорідних хвильових рівнянь для електромагнітних потенціалів. Запізнілі потенціали

В цьому розділі ми розглянемо характер рішень неоднорідних хвильових рівнянь для електромагнітних потенціалів:

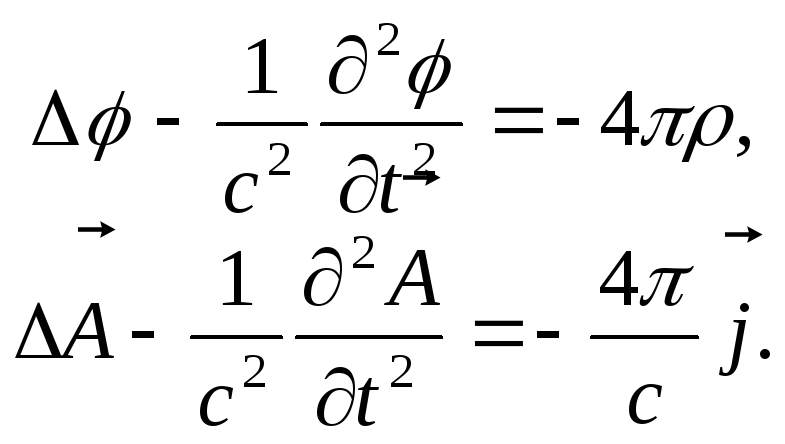(10.1)

З теорії лінійних диференціальних рівнянь в часткових похідних відомо, що в загальному випадку рішення рівнянь (10.1) мають структуру:

, (10.2)

де і є загальними рішеннями однорідних хвильових рівнянь:

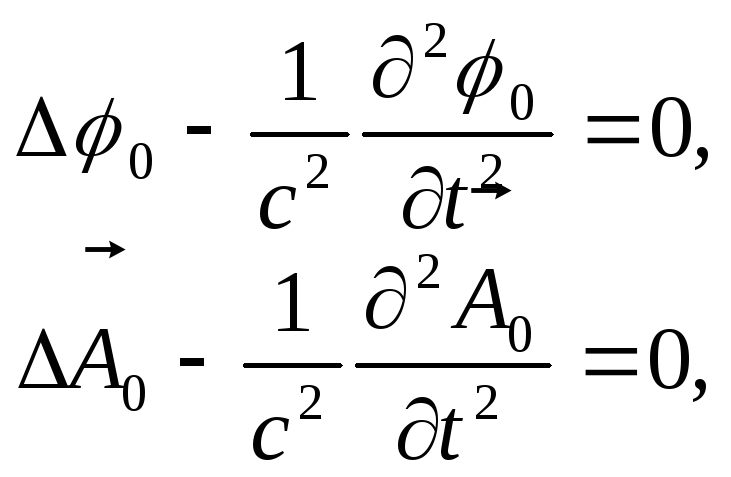(10.3)

а і є частковими рішеннями неоднорідних хвильових рівнянь:

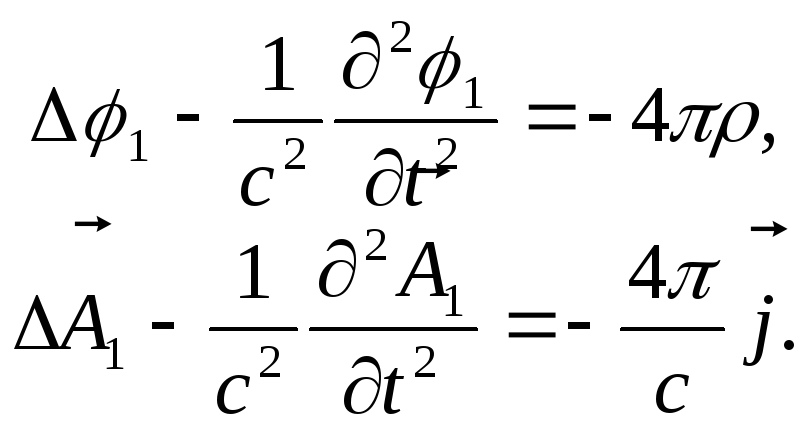(10.4)

Така побудова рішень вихідних рівнянь (10.1) передбачає, що рішення і однорідних хвильових рівнянь (10.3) задовольняють загальним граничним умовам:

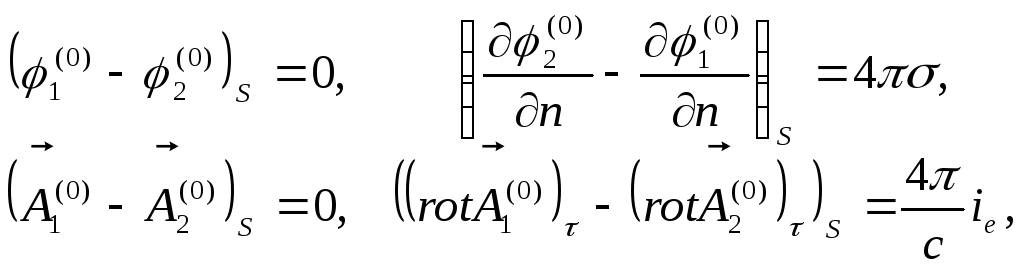(10.5)

а і - тривіальним граничним умовам:

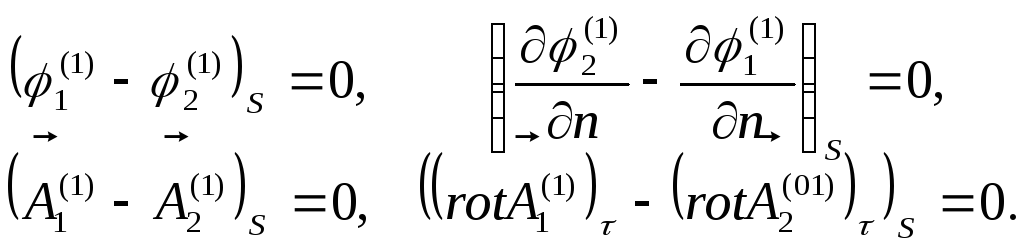(10.6)

Тут індекс «» при потенціалах піднято вгору.

Перейдемо тепер до побудови часткових рішень для неоднорідних хвильових рівнянь (10.4). Як завжди, будемо вважати, що заряди і токи розподілені по об’єму .

а) Запізнілий скалярний потенціал зовні малої однорідно зарядженої кулі

Нехай електричне поле утворюється однорідно зарядженою кулею радіусу , центр якої співпадає з початком системи координат. Будемо вважати, що заряд кулі змінюється з часом: . Зовні кулі () скалярний потенціал

задовольняє рівнянню:

. (10.7)

В подальшому для спрощення опису нижній індекс «» будемо опускати.

Оскільки куля є однорідно зарядженою, потенціал повинен бути сферично симетричним, тобто залежати тільки від відстані від центру кулі: . По тій же причині в операторі Лапласа треба залишити тільки його радіальну частину: . Використовуючи стандартну заміну змінної , тривимірне хвильове рівняння (10.7) можна перетворити в одномірне хвильове рівняння:

. (10.8)

В загальному випадку його рішення має структуру:

,

де і - довільні функції. Вони описують дві хвилі, одна з яких () розповсюджується від зарядженої кулі, друга () – в зворотному напрямку. Дійсно, фіксовані значення функції для першої хвилі спостерігаються в точках (), яким відповідають постійні значення фази () хвилі:

,

де є константою розмірності часу. Звідси випливає, що постійні значення функції не є фіксованими у просторі, а віддаляються від зарядженої кулі зі швидкістю :

. (10.9)

Інакше кажучи, фазовими поверхнями хвилі є сферичні поверхні, які віддаляються від центра за законом (10.9). фазовими поверхнями хвилі є сферичні поверхні, які віддаляються від центра. Навпаки, фазові поверхні хвилі , які також є сферами, сходяться до центра за подібним законом:

. (10.10)

Як наслідок, скалярний потенціал є сумою розбіжної і збіжної хвиль:

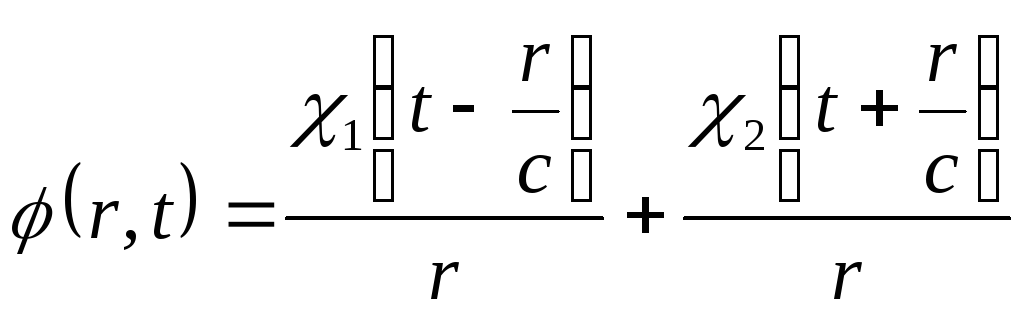, (10.11)

амплітуди яких зменшуються і зростають за законом відповідно.

Тут важливо звернути увагу на те, що внесок 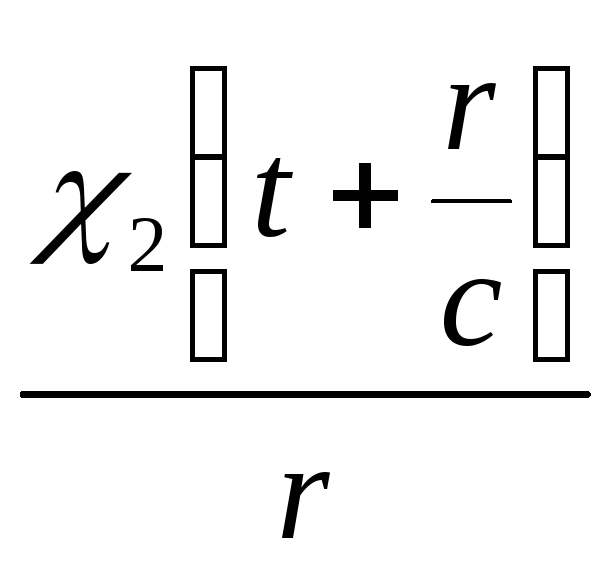суперечить принципу причинності (див. розділ 4), оскільки значення потенціалу в момент визначаються значеннями функції , які беруться в момент часу , майбутньому по відношенню до . Внаслідок цього він повинен бути відкинутим. На відміну від цього, момент часу , який відповідає хвилі , передує моменту спостереження і цілком узгоджується з принципом причинності.

Для знаходження явного вигляду функції розглянемо значення потенціалу поблизу зарядженої кулі. В цьому випадку часом запізнення електромагнітного сигналу можна знехтувати і його потенціал представити у вигляді:

. (10.12)

З другого боку, з фізичної точки зору зрозуміло, що поблизу однорідно зарядженої кулі значення потенціалу повинно визначатись законом Кулона:

. (10.13)

Порівнюючи, (10.12) і (10.13), можна заключити, що функція дорівнює: , тобто потенціал однорідно зарядженої кулі зовні неї дорівнює:

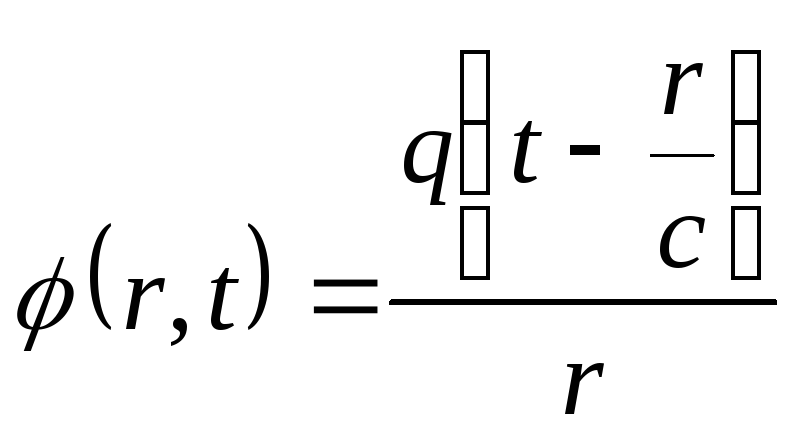. (10.14)

Як бачимо, він зберігає структуру потенціалу електростатичного поля зарядженої кулі і відрізняється тільки тим, що значення заряду береться в попередній момент часу, який відрізняється від часу спостереження на величину часу запізнення електромагнітного сигналу. Рішення однорідного хвильового рівняння (10.7) у такій формі прийнято називати запізнілим потенціалом.

Якщо центр однорідно зарядженої кулі не співпадає з початком координат, а знаходиться в точці , в формулі (10.14) достатньо зробити тривіальні заміни: в лівій частині , а в правій частині . Це пояснюється тим, що значення потенціалу в точці спостереження, згідно (10.14), залежить тільки від відстані до центру зарядженої кулі. Тоді

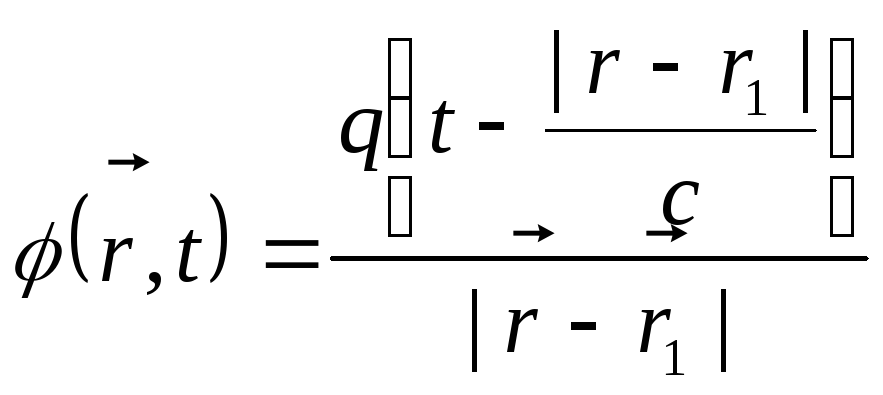. (10.15)

б) Запізнілий скалярний потенціал, утворений зарядженою системою

Нехай заряд системи розподілений за законом по об’єму . Для знаходження її запізнілого потенціалу скористаємось наступними міркуваннями:

1. на першому кроці розіб’ємо систему на сукупність сферичних областей, радіус яких є набагато меншим від характерного масштабу зміни густини заряду;

2. знайдемо внесок у потенціал, утворений кожною кулеподібною областю;

3. скориставшись принципом суперпозиції, перейдемо від суми потенціалів сферичних областей до запізнілого потенціалу системи.

У згоді з цим планом і (10.15), напишемо явний вигляд потенціалу, утвореного ю сферичною областю:

.

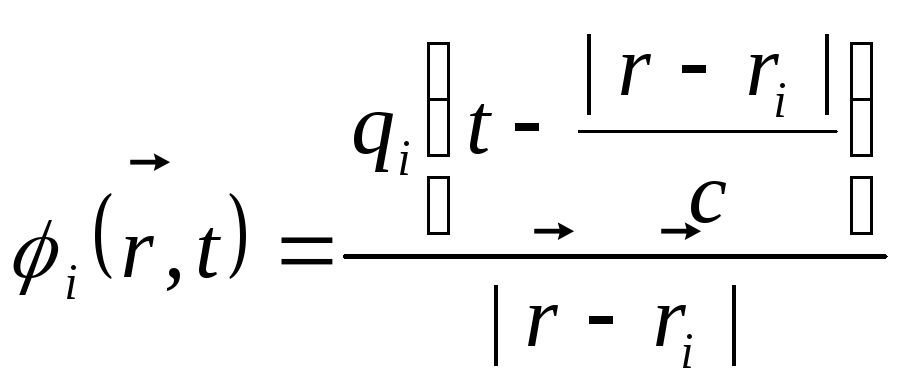Величина заряду ї сферичної області пов’язана з густиною розподілу зарядів стандартним співвідношенням:

,

де - об’єм ї області. Таким чином, попередня формула переходить у

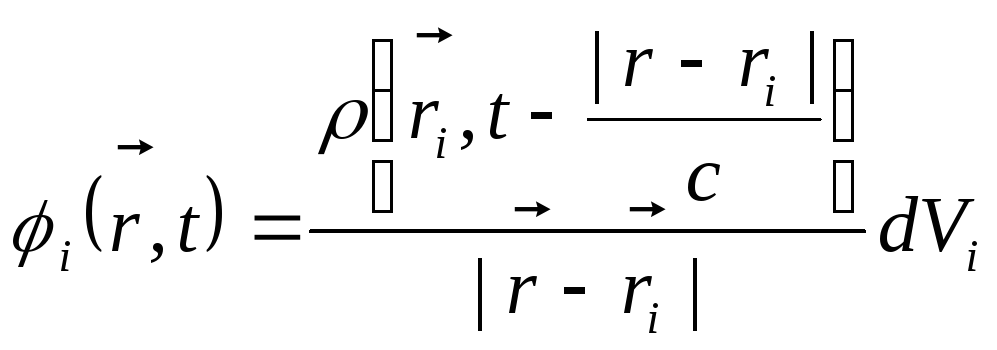. (10.16)

Згідно пункту 3) нашого плану, запізнілий потенціал системи у довільній точці зовні неї повинен дорівнювати:

.

При цю суму можна розглядати як інтегральну суму і переписати її у вигляді інтегралу:

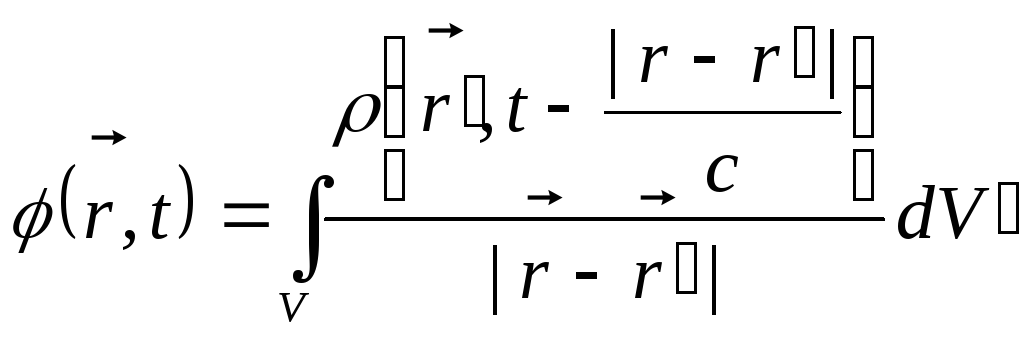. (10.17)

Давайте тепер впевнимось, що потенціал (10.17) задовольняє рівнянню (10.4) як зовні, так і всередині системи. Для цього, перш за все, розрахуємо результат дії оператора Лапласа на запізнілий потенціал (10.17):

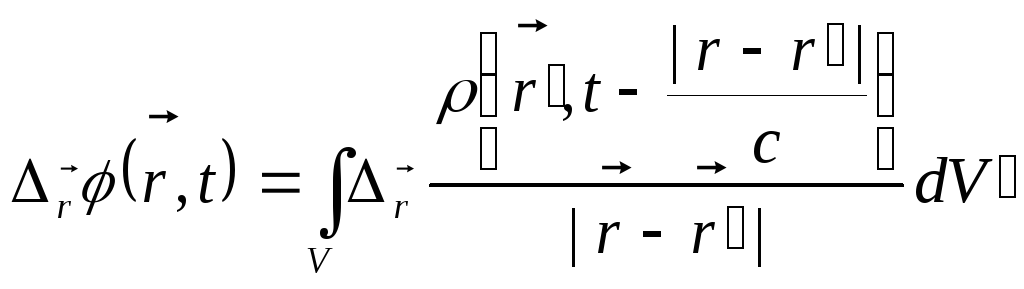. (10.18)

Тут враховано, що операції диференціювання за змінною та інтегрування за змінною є комутативними. Оскільки, , то розрахунок дії оператора Лапласа на функцію, яка стоїть справа від нього, зводиться до розрахунку послідовних дій двох операторів набла. На першому кроці:

.

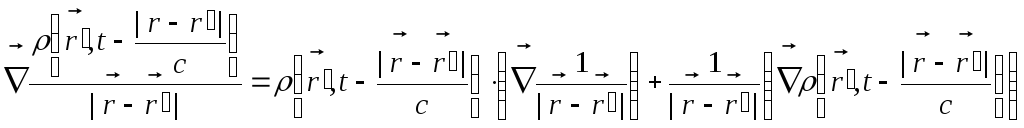Застосовуючи оператор набла вдруге, отримуємо:

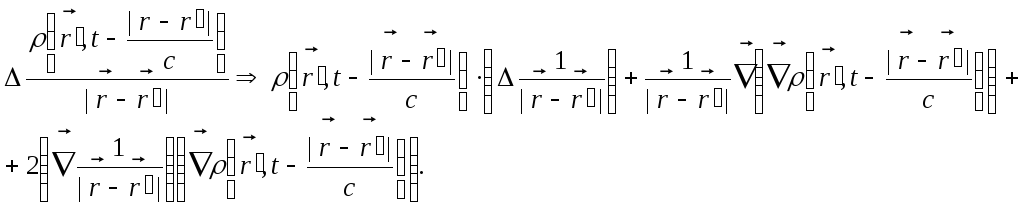
Тепер врахуємо, що мають місце наступні співвідношення:

,

,

і

.

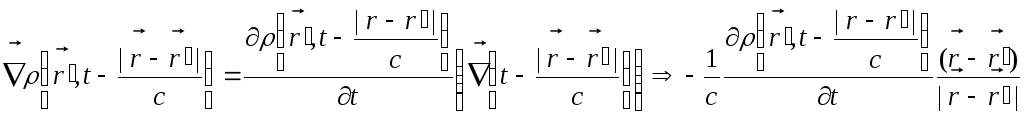За їх допомогою знаходимо:

. (10.19)

Підставимо (10.18) в (10.19). Скориставшись властивостями дельта-функції Дірака і комутативністю операцій інтегрування за просторовою змінною і диференціюванням за часом, , приходимо до наступного результату:

Таким чином, запізнілий потенціал (10.17), побудований на основі не строгих фізичних міркувань, дійсно, задовольняє 1) однорідному хвильовому рівнянню (10.7) зовні області і 2) неоднорідному хвильовому рівнянню (10.4) всередині області . Тобто, формула (10.17) є математично коректним частковим рішенням неоднорідного хвильового рівняння (10.4).

в) Запізнілий векторний потенціал, утворений системою розподілених токів

Рівняння (10.4) для скалярного і векторного потенціалів мають абсолютно однакову структуру. Тому, запізнілий векторний потенціал повинен бути цілком подібним до скалярного потенціалу (10.17):

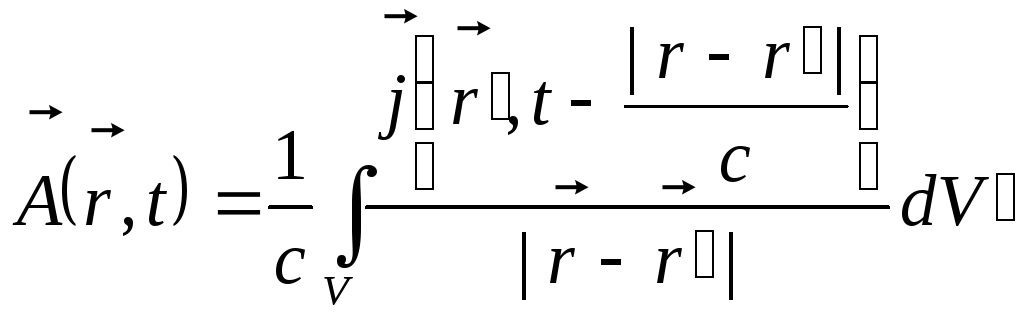. (10.20)

Тут доречно задати питання, а чи задовольняють запізнілі потенціали калібрувальній умові Лоренца (9.5)? З цією метою обчислимо :

.

Скористаємось перетворенням Лежандра:

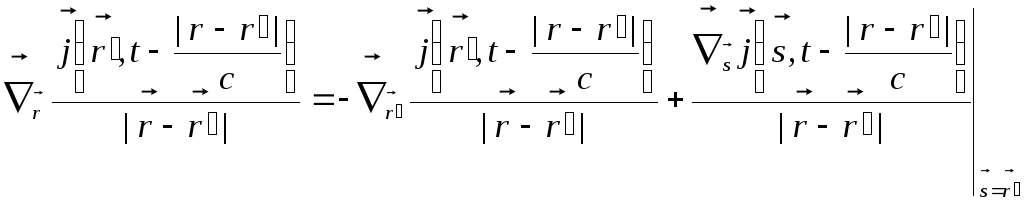(10.21)

Внесок першого додатку в (10.21) прямує до нуля. Дійсно, за теоремою Гауса-Остроградського

,

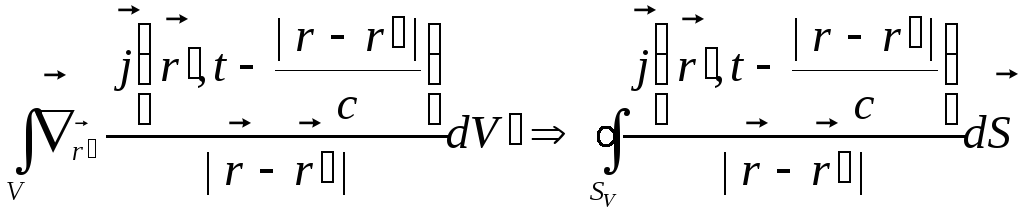де поверхня співпадає з поверхнею, яка обмежує об’єм . Але її можна і віддалити від границь об’єму . На віддалених поверхнях , тому поверхневий інтеграл приймає нульове значення. Звідси знаходимо:

.

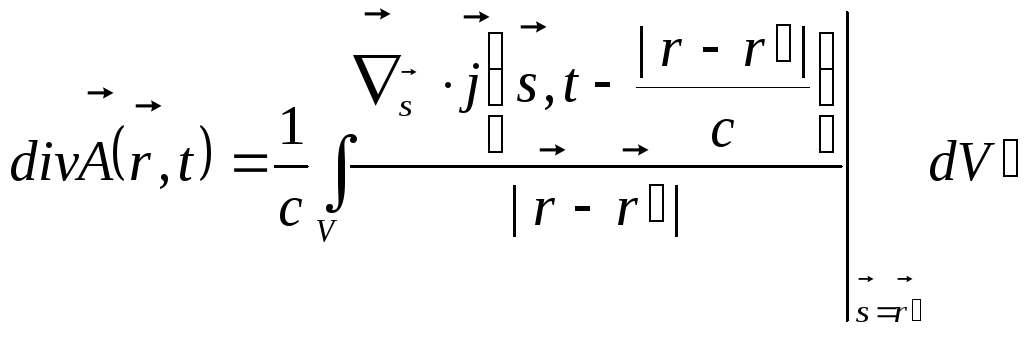З диференціальної форми закону збереження заряду випливає:

,

тому

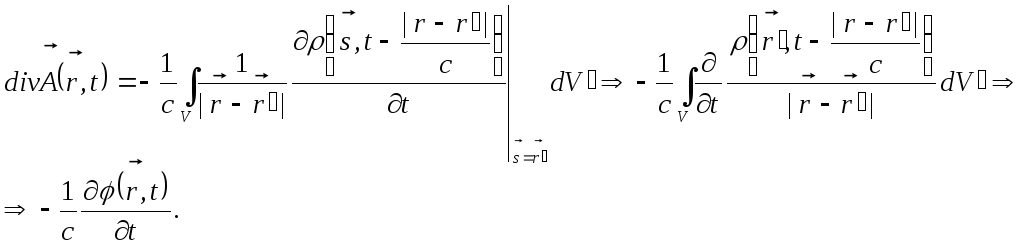
Бачимо, що запізнілі скалярний і векторний потенціали електромагнітного поля задовольняють калібрувальній умові Лоренца.

г) Функція Гріна електромагнітного поля в ССК

Представимо скалярний потенціал електромагнітного поля у вигляді:

. (10.22)

Зіставляючи його з виразом (10.17) для запізнілого скалярного потенціалу, знаходимо:

. (10.23)

Оскільки дельта-функція має властивість (див. ()), то функцію можна переписати також у вигляді:

. (10.24)

Неважко впевнитись, що вона задовольняє хвильовому рівнянню:

. (10.25)

Дійсно, якщо густину заряду у вихідному хвильовому рівнянні (10.4) для скалярного потенціалу взяти у вигляді , то , як випливає з формули (10.22), буде співпадати з функцією :

, (10.26)

тобто, повинна задовольняти тому ж самому рівнянню.

Згідно означення (10.22), функція є функцією Гріна хвилевого рівняння для скалярного потенціалу в нескінченому просторі в ССК. За своїм смислом, функція Гріна описує скалярний потенціал електромагнітного поля, утворений точковим позитивним зарядом, який виникає на одну мить в точці в момент часу . Потенціал такого поля є відмінним від нуля в нескінченно тонкому сферичному шарі, який віддаляється від точки зі швидкістю :

. (10.27)

Запізнілий векторний потенціал допускає аналогічне представлення:

. (10.28)

Якщо тік утворюється точковим позитивним зарядом, який виникає на одну мить в точці в момент часу і має миттєву швидкість , то

і

. (10.29)

Зазначимо, що характер залежності функції Гріна (10.24) від просторових координат і часу повністю узгоджується з властивостями симетрії. Дійсно, якщо простір, в якому розповсюджується електромагнітна хвиля, є однорідним і ізотропним, а час однорідним, то функція Гріна

повинна залежати від модуля різниці радіус-векторів і різниці значень часу:

. (10.29)

Саме такий характер залежності від змінних і є властивим функції Гріна (10.24).

д) Електромагнітні потенціали на великих відстанях від системи

Розглянемо скалярний і векторний потенціали на відстанях , де - діаметр системи зарядів і токів. У згоді з (10.17) і (10.20) асимптотична поведінка потенціалів визначається внесками:

, (10.30)

де , - заряд системи,

-

її дипольний момент і

.

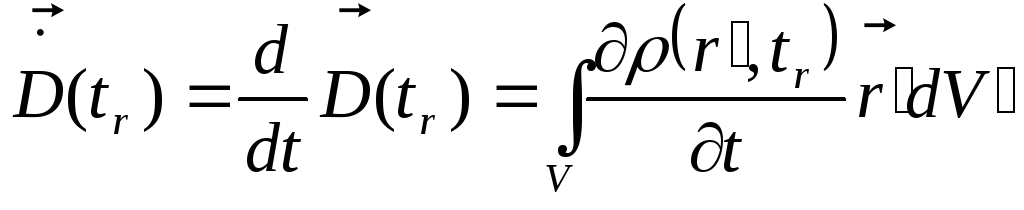Оскільки із закону збереження заряду випливає, що , то

.

Тут враховується, що з допомогою теореми Гауса-Остроградського об’ємний інтеграл можна перетворити в поверхневий:

.

Обернення останнього інтегралу в нуль пов’язано з тим, що нормальна складова току через поверхню, яка обмежує систему, дорівнює нулю. Крім того, приймається до уваги, що , де - - орт ДСК. Остаточно,

. (10.31)

Приймаючи до уваги (10.31), асимптотичну поведінку векторного потенціалу можна представити аналогічною формулою:

. (10.32)