
Для студентов / Лекции / (2)ВЕД / (12)Мультипольні розклади в електростатиці
.doc12. Мультипольні розклади в електростатиці
В цьому розділі будуються мультипольні розклади для наступних задач електростатики: 1) потенціалу компактної системи зарядів на великих відстанях від неї (систему зарядів називають компактною, якщо відстань між найвіддаленішими один від одного зарядами є скінченою); 2) енергії взаємодії компактної сукупності зарядів із зовнішнім електричним поле, яке плавно змінюється на протязі системи і 3) енергії взаємодії між двома компактними системами зарядів на відстанях, які набагато перевищують значення діаметрів систем.
В
усіх цих випадках можна написати точні
вирази для і для потенціалу систему і
для енергій взаємодії. Так потенціал
системи
![]() зарядів на довільних відстанях від неї
задається стандартним співвідношенням:
зарядів на довільних відстанях від неї
задається стандартним співвідношенням:
![]() .
(12.1)
.
(12.1)
Але
на великих відстанях від системи, в
нульовому наближені вона може розглядатись
як точково-подібна, а її потенціал
апроксимуватись сумарним зарядом
системи
![]() :
:
![]() ,
(12.2)
,
(12.2)
де
![]() .
Це є наближення, в якому всі заряди
системи знаходяться в одній і тій же
точці – на початку координат. Зрозуміло,
що невеличкий зсув зарядів з початку
координат бути призводити до появи
внесків, які будуть убувати з відстанню
за більш високими степенями
.
Це є наближення, в якому всі заряди
системи знаходяться в одній і тій же
точці – на початку координат. Зрозуміло,
що невеличкий зсув зарядів з початку
координат бути призводити до появи
внесків, які будуть убувати з відстанню
за більш високими степенями
![]() :
:
![]() ,
(12.3)
,
(12.3)
де
![]() -
певні коефіцієнти, які будуть визначені
нижче. Така ж сама обставина буде
проявлятись і в інших сформульованих
вище задачах.
-
певні коефіцієнти, які будуть визначені
нижче. Така ж сама обставина буде
проявлятись і в інших сформульованих
вище задачах.
а) Мультипольний розклад потенціалу компактної системи зарядів
Нехай
![]() позначає
діаметр системи зарядів. В цьому випадку
всі
позначає
діаметр системи зарядів. В цьому випадку
всі
![]() .
Розглянемо асимптотичну поведінку
потенціалу
.
Розглянемо асимптотичну поведінку
потенціалу
![]() ,
який задається формулою (12.1)
на
відстанях
,
який задається формулою (12.1)
на
відстанях
![]() від системи, які задовольняють нерівності:
від системи, які задовольняють нерівності:
![]() .
Завдяки нерівності
.
Завдяки нерівності
![]() ,
обернену
відстань
,
обернену
відстань
![]() можна
розкласти в нескінчений ряд за степенями
компонентів вектора
можна
розкласти в нескінчений ряд за степенями
компонентів вектора
![]() .
Згідно
(Д.10)
відповідний розклад має структуру:
.
Згідно
(Д.10)
відповідний розклад має структуру:
![]() .
(12.4)
.
(12.4)
Підставляючи його в (12.1), знаходимо:
![]() ,
,
або
![]() ,
(12.5)
,
(12.5)
де коефіцієнти розкладу дорівнюють:
 (12.6)
(12.6)
Як
бачимо, вони мають смисл тензорів
нульового, першого, другого і т.п. рангу,
оскільки за структурою є суперпозиціями
тензорних комбінацій
![]() ,
утворених з добутків компонентів
радіус-вектора
,
утворених з добутків компонентів
радіус-вектора
![]()
![]() го
заряду. Прийнято називати:
го
заряду. Прийнято називати:
![]() - компонентами вектора дипольного
моменту,
- компонентами вектора дипольного
моменту,
![]() -
компонентами тензора квадрупольного
моменту і т.д. Вирази (12.6) побудовані за
тим же принципом, що і моменти сили, що
діє на систему.
-
компонентами тензора квадрупольного
моменту і т.д. Вирази (12.6) побудовані за
тим же принципом, що і моменти сили, що
діє на систему.
Формулу (12.5) часто записують у вигляді:
![]() ,
(12.7)
,
(12.7)
де
![]() -
(12.8)
-
(12.8)
вектор дипольного моменту,
![]() -
-
компоненти модифікованого тензору квадрупольного моменту. Його характерною властивістю є те, що сума його діагональних елементів – слід матриці – дорівнює нулю:
![]() .
.
Еквівалентність
двох різних означень
![]() витікає
з того, що їх згортки з тензором
витікає
з того, що їх згортки з тензором
![]() є однаковими:
є однаковими:
![]() .
.
Завдяки цьому, в залежності від ситуації ми будемо користуватись то одним, то другим означень тензора квадрупольного моменту зарядів.
Якщо електричне поле утворюється не дискретними, а розмазаними зарядами, означення мультипольних моментів розподілу зарядів змінюються тривіальним чином (замість сум з’являються інтеграли):
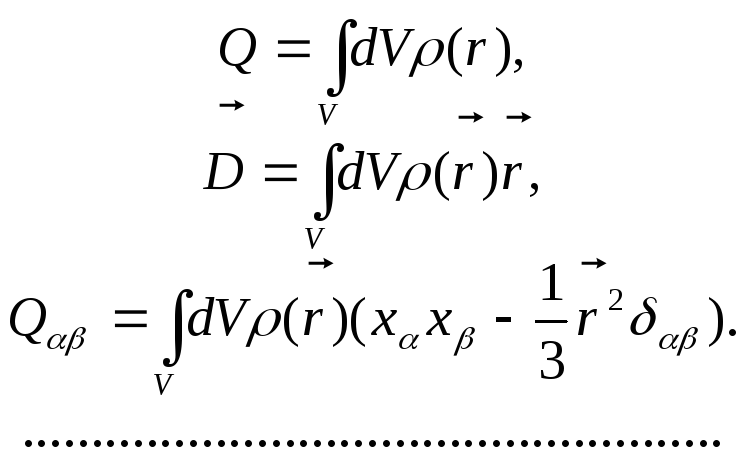 (12.9)
Проілюструємо
застосування
отриманих формул на прикладі простої
задачі, в якій стандартний метод
розрахунку потенціалу виявляється
нетривіальним.
(12.9)
Проілюструємо
застосування
отриманих формул на прикладі простої
задачі, в якій стандартний метод
розрахунку потенціалу виявляється
нетривіальним.
Задача.
Визначити
потенціал електричного поля, утвореного
рівномірно зарядженим кругом на великих
відстанях від нього. Радіус круга
![]() ,
густина заряду
,
густина заряду
![]() .
.
Розв’язок: Загальна відповідь тут може бути написаною без утруднень:
![]() .
.
Але при довільній орієнтації диска значення інтегралу зводиться до еліптичної функції.
Проте, на великих відстанях від круга значно природніше скористатись розкладом потенціалу в ряд за мультиполями:
![]() ,
(12.10)
,
(12.10)
де
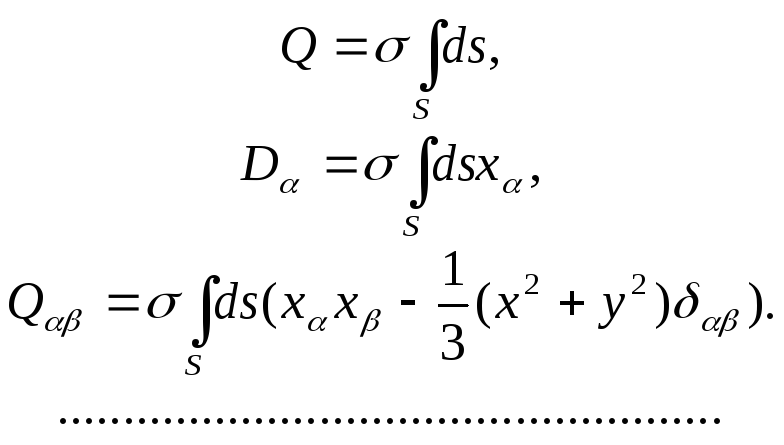 (12.11)
(12.11)
є
мультипольними моментами у власній
системі координат круга, коли вважається,
що круг знаходиться в площині (![]() ),
а його центр співпадає з початком
координат. Значення нульового
мультипольного моменту – заряду –
знаходиться тривіально:
),
а його центр співпадає з початком
координат. Значення нульового
мультипольного моменту – заряду –
знаходиться тривіально:
![]() .
.
Для
визначення мультипольних моментів
більш високого порядку бажано, перш за
все, скористатись властивостями симетрії
у розподілі заряду. Очевидно, що
![]() .
Оскільки в площині (
.
Оскільки в площині (![]() )
розподіл заряду є ізотропним, а початок
координат є водночас і центром інверсії,
то
)
розподіл заряду є ізотропним, а початок
координат є водночас і центром інверсії,
то
![]() -
компоненти дипольного моменту повинні
задовольняти співвідношенню:
-
компоненти дипольного моменту повинні
задовольняти співвідношенню:![]() .
З
тих самих причин можна стверджувати,
що
дорівнюють
нулю
і
всі непарні мультипольні моменти більш
високого порядку.
.
З
тих самих причин можна стверджувати,
що
дорівнюють
нулю
і
всі непарні мультипольні моменти більш
високого порядку.
Що
стосується компонентів квадрупольного
моменту, то внаслідок симетрії у розподілі
заряду відмінними від нуля повинні бути
тільки діагональні моменти матриці
![]() :
:
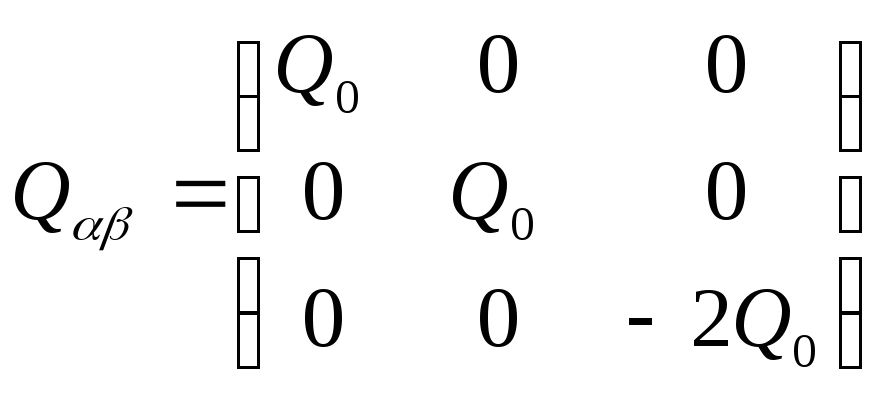 .
(12.12)
.
(12.12)
Більш
конкретно, рівняння
![]() є наслідком ізотропії у розподілу заряду
в площині (
є наслідком ізотропії у розподілу заряду
в площині (![]() ),
а рівняння
),
а рівняння
![]() є
наслідком обернення сліду матриці
є
наслідком обернення сліду матриці
![]() до
нуля. Безпосередньо з (12.11) випливає, що
до
нуля. Безпосередньо з (12.11) випливає, що
![]() .
.
Діагональну матрицю (12.12), очевидно, можна переписати у вигляді:
![]() .
(12.13)
.
(12.13)
Підставляючи (12.13) і отримані вище значення заряду і дипольного моменту у (12.10), для потенціалу електричного поля у квадрупольному наближенні знаходимо:
 .
.
Оскільки
![]() ,
де
,
де
![]() -
одиничний
вектор, перпендикулярний до площини
кругу, то для потенціалу остаточно
знаходимо:
-
одиничний
вектор, перпендикулярний до площини
кругу, то для потенціалу остаточно
знаходимо:
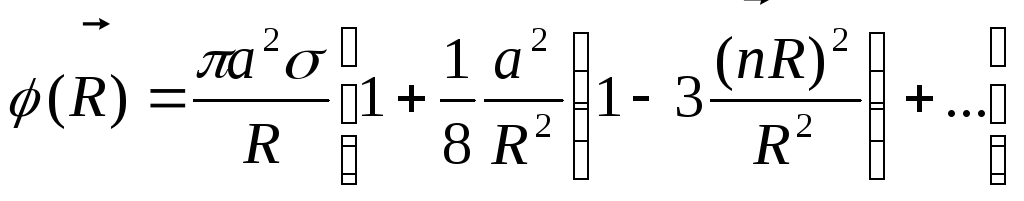 .
(12.14)
.
(12.14)
б) Енергія взаємодії компактної сукупності зарядів із зовнішнім електричним поле, яке плавно змінюється на протязі системи
Енергія
взаємодії сукупності зарядів із зовнішнім
електричним полем, яке описується
потенціалом
![]() ,
визначається стандартним виразом:
,
визначається стандартним виразом:
![]() ,
(12.15)
,
(12.15)
в
якому![]() позначає певну фіксовану точку всередині
системі, а
позначає певну фіксовану точку всередині
системі, а
![]() є
радіус-вектором
є
радіус-вектором
![]() -го
заряду
відносно точки
-го
заряду
відносно точки
![]() .
Якщо діаметр системи
.
Якщо діаметр системи
![]() є
малим у порівнянні з характерним
масштабом
є
малим у порівнянні з характерним
масштабом
![]() зміни
зовнішнього поля, то його потенціал
зміни
зовнішнього поля, то його потенціал
![]() доцільно
розкласти в ряд за степенями
доцільно
розкласти в ряд за степенями
![]() :
:
![]()
Оскільки,
![]() ,
,
![]() ,
,
то енергію взаємодії (12.15) можна переписати у вигляді:
![]() ,
,
або
![]() .
(12.16)
.
(12.16)
Тут,
як і раніше,
![]() позначають повний заряд системи,
дипольний і квадрупольний моменти
відповідно. Приймаючи до уваги, що
заряди, які утворюють зовнішнє поле,
знаходяться за межами заданої системи
зарядів, задовольняють рівнянню:
позначають повний заряд системи,
дипольний і квадрупольний моменти
відповідно. Приймаючи до уваги, що
заряди, які утворюють зовнішнє поле,
знаходяться за межами заданої системи
зарядів, задовольняють рівнянню:
![]() ,
,
в (12.16) можна перейти до модифікованого квадрупольного моменту:
![]() (12.17)
(12.17)
В
тих випадках, коли положення фіксованої
точки
![]() можна обрати таким чином, щоб
можна обрати таким чином, щоб
![]() ,
формула (12.17) спрощується:
,
формула (12.17) спрощується:
![]() (12.18)
(12.18)
Зазначимо, що формула (12.17) залишається незмінною і тоді, коли заряди розподілені по системі неперервним чином, або має місце комбінація дискретних і неперервних зарядів.
в) Мультипольний розклад енергії взаємодії двох компактних систем зарядів
Нехай
відстань
![]() між двома системами зарядів значно
перевищує їх діаметри:
між двома системами зарядів значно
перевищує їх діаметри:
![]() .
В
цьому випадку електричне поле, утворене
першою системою зарядів, можна розглядати
як слабо-неоднорідне поле, в якому
знаходиться друга підсистема зарядів.
Зрозуміло, що її енергію взаємодії
.
В
цьому випадку електричне поле, утворене
першою системою зарядів, можна розглядати
як слабо-неоднорідне поле, в якому
знаходиться друга підсистема зарядів.
Зрозуміло, що її енергію взаємодії
![]() з
полем першої підсистеми можна апроксимувати
мультипольним розкладом типу (12.17):
з
полем першої підсистеми можна апроксимувати
мультипольним розкладом типу (12.17):
![]() .
(12.19)
.
(12.19)
З другого боку, згідно (12.5):
![]()
Підставляючи цей вираз, а також його похідні
 в
(12.19), бачимо що різні внески можна
згрупувати за степенями убування
в
(12.19), бачимо що різні внески можна
згрупувати за степенями убування
![]() :1
:1
![]() ,
(12.20)
,
(12.20)
де
 (12.21)
(12.21)
Ряд (12.20) прийнято називати мультипольним розкладом енергії взаємодії двох відділених компактних систем. Похідні, які входять до (12.21), приймають наступні значення:
![]()
![]()
![]()
Підставляючи їх в (12.21), остаточно знаходимо:
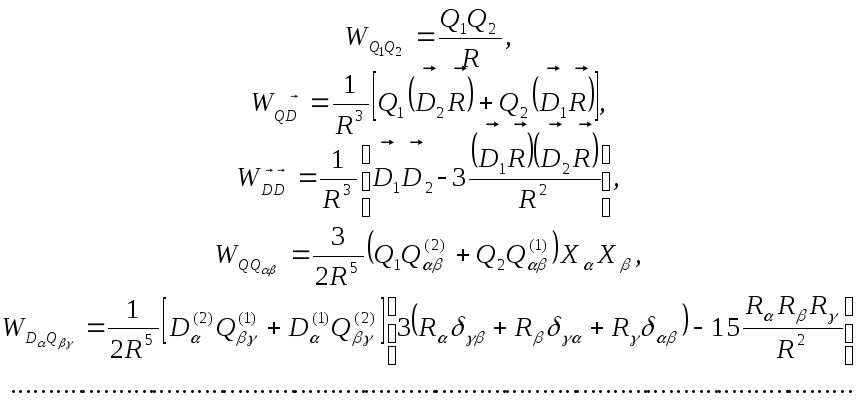 .
(12.21)
.
(12.21)
Як бачимо, закони убування диполь-дипольної і заряд-квадрупольної взаємодії є однаковими. У мультипольних внесках більш високого порядку така ситуація є типовою. Зокрема, в загальному випадку однаковий порядок величини мають квадруполь-квадрупольна, диполь-октупольна і заряд-гексапольна взаємодії.
Все
выписанные выражения должны быть
инвариантны относительно перестановки
индексов систем и одновременной замены
![]() .
.
г) Закони перетворення компонентів мультипольних моментів при зсувах початку координат і поворотах системи зарядів
Нехай
початок системи координат, в якій
розраховуються компоненти мультипольних
моментів, зсувається на вектор
![]() .
Тоді радіус-вектор
.
Тоді радіус-вектор
![]() го
заряду, змінюється за законом:
го
заряду, змінюється за законом:
![]() .
(12.22)
.
(12.22)
За
означенням, мультипольний момент
![]() го
порядку дорівнює:
го
порядку дорівнює:
![]() ,
,
що у символічній формі можна переписати у вигляді:
![]() ,
(12.23)
,
(12.23)
де
комбінація
![]() є
прямим добутком
є
прямим добутком
![]() векторів
векторів
![]() .
Підставляючи (12.22) в (12.23), знаходимо:
.
Підставляючи (12.22) в (12.23), знаходимо:
![]() ,
(12.24)
,
(12.24)
де
![]() ,
а символ
,
а символ
![]() означає симетризацію за індексами:
означає симетризацію за індексами:
![]() ,
,
![]() ,
,
і т.д. У такий спосіб знаходимо, що перші мультипольні моменти перетворюються за закономи:
 (12.25)
(12.25)
Якщо користуватись модифікованим квадрупольним моментом, то третя строчка в (12.25) набуває вигляду:
![]() .
(12.26)
.
(12.26)
При
повороті системи зарядів на малий кут
![]() навколо вісі, просторова орієнтація
якої задається ортом
навколо вісі, просторова орієнтація
якої задається ортом
![]() ,
радіус-вектор
,
радіус-вектор
![]() го
заряду змінюється за законом:
го
заряду змінюється за законом:
![]() ,
,
що в компонентах переписується наступним чином:
![]()
Діючи
далі у такий самий спосіб, як і в
попередньому випадку, і утримуючи тільки
лінійні за
![]() внески,
знаходимо:
внески,
знаходимо:
 (12.27)
(12.27)
д) Інваріантність потенціалу відносно зсуву початку координат
З фізичної точки зору є цілком очевидним, що значення потенціалу компактної системи зарядів у деякій віддаленій точці не повинно залежати від вибору початку координат всередині системи. Інакше кажучи, асимптотичні мультипольні розклади, які відповідають різним системам координат, повинні задовольняти рівнянню:
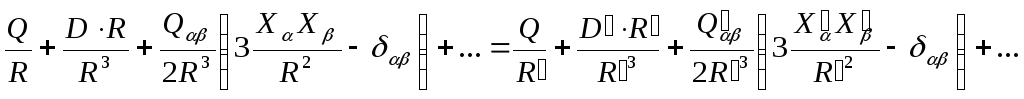 ,
(12.28)
,
(12.28)
в
якому
![]() ,
а мультипольні моменти пов’язані між
собою перетвореннями (12.24) або (12.25).
Переконаємось у справедливості (12.28),
виділяючи і сумуючи всі внески, які
убувають за однаковим законом
,
а мультипольні моменти пов’язані між
собою перетвореннями (12.24) або (12.25).
Переконаємось у справедливості (12.28),
виділяючи і сумуючи всі внески, які
убувають за однаковим законом
![]() Зупинимось тут тільки на внесках
нульового і першого порядку за відношенням
Зупинимось тут тільки на внесках
нульового і першого порядку за відношенням
![]() .
В цьому наближенні,
.
В цьому наближенні,
![]()
 ,
,
і
т.д. Зрозуміло, що в нульовому за
![]() наближенні права частина формули (12.28)
переходить в її ліву частину:
наближенні права частина формули (12.28)
переходить в її ліву частину:
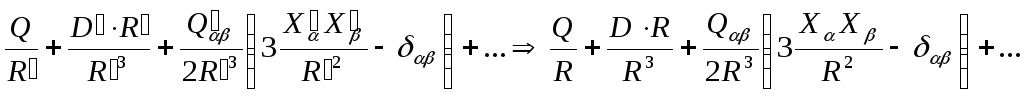
В першому наближенні перший і другий додатки в (12.28) породжують внески:
![]() ,
,
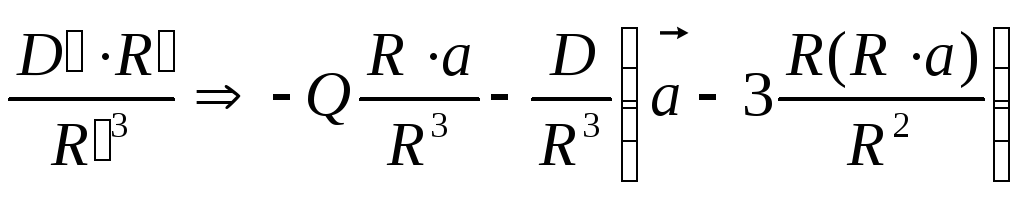 .
.
З третього додатку виділимо тільки внесок, пропорційний дипольному моменту:
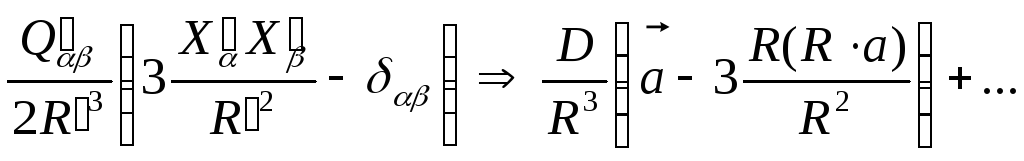
Неважко
бачити, що внески у потенціал системи,
обумовлені зарядом і дипольним моментом,
у лінійному за відношенням
![]() наближенні взаємно компенсуються. Так
само можна переконатись в існуванні
взаємної компенсації всіх внесків,
пропорційних старшим мультипольним
моментам, у наближенні
наближенні взаємно компенсуються. Так
само можна переконатись в існуванні
взаємної компенсації всіх внесків,
пропорційних старшим мультипольним
моментам, у наближенні
![]() ,
а також у всіх інших наближеннях більш
високого порядку.
,
а також у всіх інших наближеннях більш
високого порядку.
Таким чином, вибір початку координат не впливає на значення потенціалу. Цей результат залишається справедливим і для мультипольних розкладів енергій взаємодії компактної системи зарядів зі слабо неоднорідним зовнішнім електричним полем і віддалених компактних систем зарядів.
Математичний
додаток. Розклад довільної скалярної
функції
![]() в ряд Тейлора за компонентами вектора
в ряд Тейлора за компонентами вектора
![]() .
.
У порівнянні з розкладом скалярної функції однієї змінної:
![]() (Д1)
(Д1)
розклад
функції
![]() від векторного аргументу
від векторного аргументу
![]() в
ряд Тейлора є більш складним, оскільки
векторам
в
ряд Тейлора є більш складним, оскільки
векторам
![]() і
і
![]() відповідають по три незалежні компоненти:
відповідають по три незалежні компоненти:
![]() і
і
![]() .
В цьому випадку потрібно диференціювати
функцію по всім трьом компонентам і
похідні множити на відповідну комбінацію
приростів аргументу:
.
В цьому випадку потрібно диференціювати
функцію по всім трьом компонентам і
похідні множити на відповідну комбінацію
приростів аргументу:
![]() (Д2)
(Д2)
Тут, як і завжди, по двом індексам, що повторюються, виконується сумування. Зокрема
![]()
Похідні
від функції
![]() обчислюються з урахуванням того, що
вона залежить від модуля радіус-вектора
обчислюються з урахуванням того, що
вона залежить від модуля радіус-вектора
![]() .
Приймаючи до увагу цю обставину,
обчислюємо похідні за правилами, які
застосовуються при диференціюванні
функції, яка залежить від аргументу
складним чином. Послідовно знаходимо:
.
Приймаючи до увагу цю обставину,
обчислюємо похідні за правилами, які
застосовуються при диференціюванні
функції, яка залежить від аргументу
складним чином. Послідовно знаходимо:
![]() ,
(Д3)
,
(Д3)
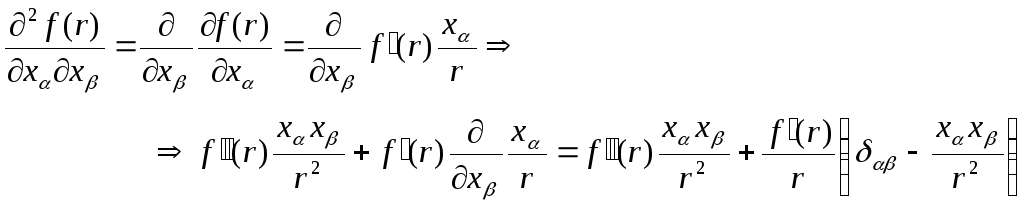 ,
(Д4)
,
(Д4)
![]()
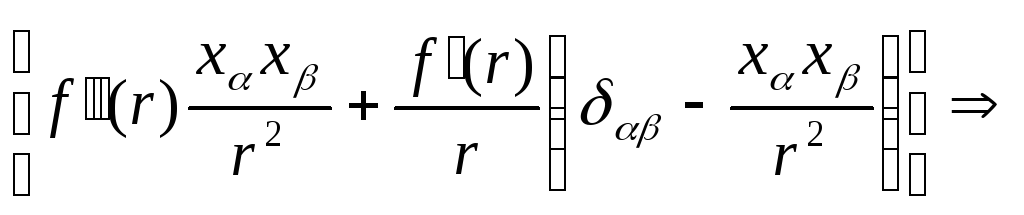
 .
(Д5)
.
(Д5)
Так само знаходяться і похідні більш високого порядку.
Розглянемо
найбільш прості випадки застосування
отриманих формул. Нехай
![]() .
Тоді
.
Тоді
![]() ,
,
![]() ,
,
![]() ,
,
і
для функції
![]() має місце наступний розклад:
має місце наступний розклад:
![]() .
(Д6)
.
(Д6)
У векторній формі він приймає більш зручний вигляд:
 (Д7)
(Д7)
Для
побудови розкладу в ряд Тейлора
спорідненої функції
![]() ,
достатньо ряди (Д6) або (Д7) возвести до
квадрату. Зокрема, за допомогою (Д7)
отримуємо:
,
достатньо ряди (Д6) або (Д7) возвести до
квадрату. Зокрема, за допомогою (Д7)
отримуємо:
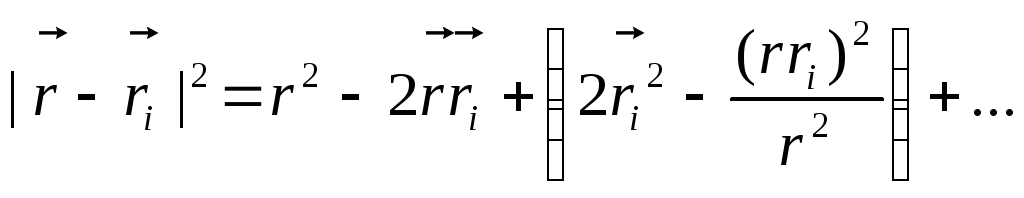
Для
оберненої функції
![]() перші три похідні дорівнюють:
перші три похідні дорівнюють:
![]() ,
,
![]() ,
(Д8)
,
(Д8)
![]() .
(Д9)
.
(Д9)
Перші
члени розкладу функції в ряд Тейлора
за степенями компонентів
![]() ,
таким чином, дорівнюють:
,
таким чином, дорівнюють:
![]() (Д10)
(Д10)
