
Для студентов / Лекции / (2)ВЕД / (15)Закон збереження енергії електромагнітного поля
.doc14. Закон збереження енергії електромагнітного поля
Для опису властивостей електромагнітного поля ми часто використовуємо векторні лінії. Проте з самого початку підкреслюється, що векторні лінії є вдалим способом зображення просторового розподілення електричного і магнітного полів. Роль векторних ліній є такою самою, як і роль паралелей і меридіанів на поверхні глобуса. В природі вони відсутні, але їх введення допомагає нам просто задати координати точки чи області на земній поверхні. У зв’язку з цим виникає питання, а чи не є саме електромагнітне поле вдалою містифікацією, за допомогою якої багато що можна дуже просто пояснити, але яка не відповідає дійсній природі речей? У зв’язку з цим доречно згадати той факт, що сили взаємодії між нерухомими зарядами можна описати, взагалі, без притягнення поняття електростатичного поля. Тут достатньо скористатись законом Кулона, згідно якого сили взаємодії між зарядами визначаються тільки відстанями між ними. Безпосередньої необхідності у введенні електричного поля не виникає. Така ж сама ситуація є характерною для магнітостатичного поля.
Але ситуація зразу ж ускладнюється при переході до опису взаємодії рухомих електричних зарядів. Взаємодія зарядів, як ми бачили, суттєво залежать від ефектів запізнення електромагнітного поля, які є тим більш значними, чим з більшою швидкістю рухаються заряди. Це однозначно свідчить про те, що електромагнітне поле є тим безпосереднім об’єктом, який створюється зарядами і впливає на рух всіх зарядів. Сили, які діють на заряди, мають локальний характер: вони визначаються напруженостями електричного і магнітного полів в місцях знаходження зарядів. Іншими словами, електромагнітне поле, яке утворюється зарядами, стає самостійним фізичним об’єктом, яке не тільки формує сили взаємодії між зарядами, а якому притаманні всі характерні риси фізичного об’єкту: певні енергія, імпульс і момент імпульсу, а також властивості інерції і таке інше.
В цьому розділі ми детально розглянемо поведінку підсистеми зарядів і створеного ними електромагнітного поля. Будуть встановлені основні енергетичні характеристики електромагнітного поля, а також доведено, що закон збереження енергії має місце тільки по відношенню до повної системи заряди + електромагнітне поле.
а) Закон збереження енергії електромагнітного поля
Електромагнітне
поле, утворене підсистемою рухомих
зарядів
![]() описується стандартними рівняннями
Максвела (6.19), які тут ми перепишемо у
вигляді:
описується стандартними рівняннями
Максвела (6.19), які тут ми перепишемо у
вигляді:
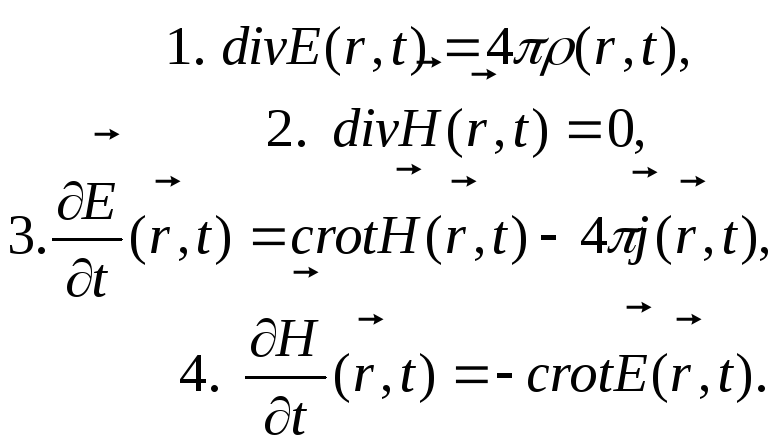 (14.1)
(14.1)
Тут
приймається, що заряди є точковими і
тому густини зарядів і токів задаються
виразами:
![]() і
і
![]() ,
де
,
де
![]() -
швидкість
-
швидкість
![]() го
заряду. Помножимо скалярним чином ліву
і праву частини 3-го і 4-го рівнянь в
(14.1) на вектори
го
заряду. Помножимо скалярним чином ліву
і праву частини 3-го і 4-го рівнянь в
(14.1) на вектори
![]() і
і
![]() відповідно, після чого утворимо їх суму:
відповідно, після чого утворимо їх суму:
![]() .
(14.2)
.
(14.2)
Неважко бачити, що
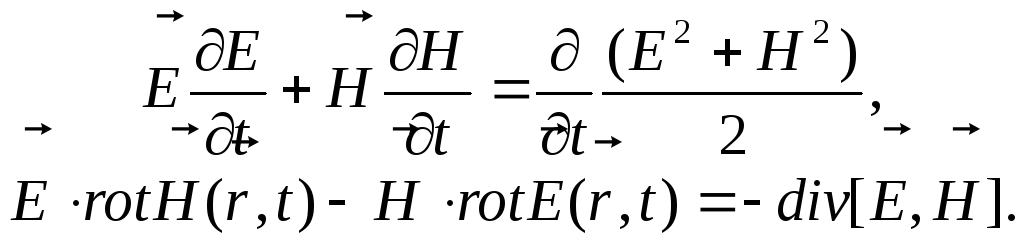 (14.3)
(14.3)
Третій
додаток в (14.2),
![]() ,
має смисл густини потужності сил, які
діють на заряджені частинки з боку
електромагнітного поля. Дійсно, розглянемо
швидкість зміни густини кінетичної
енергії підсистеми зарядів:
,
має смисл густини потужності сил, які
діють на заряджені частинки з боку
електромагнітного поля. Дійсно, розглянемо
швидкість зміни густини кінетичної
енергії підсистеми зарядів:
![]() ,
(14.4)
,
(14.4)
де
![]() - число частинок в одиниці об’єму. Тут,
у згоді з законом Ньютона
- число частинок в одиниці об’єму. Тут,
у згоді з законом Ньютона
![]() ,
а сила
,
а сила
![]() ,
яка діє на
,
яка діє на
![]() ту
заряджену частинку, прирівнюється сумі
сил, які діють на частинку з боку
електричного і магнітного полів (в
останньому випадку це буде сила Лоренца):
ту
заряджену частинку, прирівнюється сумі
сил, які діють на частинку з боку
електричного і магнітного полів (в
останньому випадку це буде сила Лоренца):
![]() .
Така можливість є цілком виправданою
у випадку, коли підсистема заряджених
частинок є розрідженою і можна повністю
знехтувати короткодіючими силами
молекулярного походження. Крім того,
враховано, що внаслідок ортогональності
швидкості частинок і сил Лоренца, їх
внесок в роботу над підсистемою частинок
дорівнює нулю. Далі, неважко зрозуміти,
що середнє значення роботи, яка виконується
електричним полем на підсистемою
заряджених частинок в одиницю часу,
зводиться до добутку густини току на
напруженість електричного поля:
.
Така можливість є цілком виправданою
у випадку, коли підсистема заряджених
частинок є розрідженою і можна повністю
знехтувати короткодіючими силами
молекулярного походження. Крім того,
враховано, що внаслідок ортогональності
швидкості частинок і сил Лоренца, їх
внесок в роботу над підсистемою частинок
дорівнює нулю. Далі, неважко зрозуміти,
що середнє значення роботи, яка виконується
електричним полем на підсистемою
заряджених частинок в одиницю часу,
зводиться до добутку густини току на
напруженість електричного поля:
![]() .
Комбінуючи (14.2) – (14.4), остаточно знаходимо:
.
Комбінуючи (14.2) – (14.4), остаточно знаходимо:
![]() ,
(14.5)
,
(14.5)
де
![]() ,
(14.6)
,
(14.6)
![]() .
(14.7)
.
(14.7)
Рівняння (14.5) є цілком ідентичним закону збереження заряду в диференціальній формі:
![]() .
(14.8)
.
(14.8)
Додамо,
що такий самий вигляд має закон збереження
маси в гідродинаміці, або інакше кажучи,
рівняння нерозривності. Це дає підстави
стверджувати, що крім законів збереження
заряду і маси в системі заряди +
електромагнітне поле має місце принаймні
ще одна незалежна величина, яка задовольняє
закону збереження. Оскільки
![]() за
смислом є густиною енергії частинок,
то можна стверджувати, що терм
за
смислом є густиною енергії частинок,
то можна стверджувати, що терм
![]() (14.9)
(14.9)
який
входить в вираз для
![]() адитивним чином, є густиною енергії
електромагнітного поля. Так само,
величина
адитивним чином, є густиною енергії
електромагнітного поля. Так само,
величина
![]() ,
яка визначається формулою (14.7), є аналогом
,
яка визначається формулою (14.7), є аналогом
![]() і
повинна тлумачитись як густина потоку
енергії електромагнітного поля.
і
повинна тлумачитись як густина потоку
енергії електромагнітного поля.
Така
інтерпретація величин
![]() і
і
![]() стає самоочевидною, коли ми розглянемо
їх явний вигляд для плоскої хвилі. В
цьому випадку в рівнянні (14.6)
стає самоочевидною, коли ми розглянемо
їх явний вигляд для плоскої хвилі. В
цьому випадку в рівнянні (14.6)
![]() ,
,
![]() і
і
![]() .
Оскільки, крім того,
.
Оскільки, крім того,
![]() ,
то
,
то
![]() ,
тобто густина потоку енергії дорівнює
густині енергії електромагнітного
поля, помноженій на швидкість розповсюдження
хвилі і одиничний вектор
,
тобто густина потоку енергії дорівнює
густині енергії електромагнітного
поля, помноженій на швидкість розповсюдження
хвилі і одиничний вектор
![]() ,
який задає її напрямок розповсюдження.
Повна еквівалентність формул (14.6) і
(14.8) свідчить, що електромагнітне поле
демонструє певні риси подібності до
ідеального суцільного середовища,
поведінка якого описується рівняннями,
що зводяться до законів збереження
маси, імпульсу, енергії і моменту
імпульсу.
,
який задає її напрямок розповсюдження.
Повна еквівалентність формул (14.6) і
(14.8) свідчить, що електромагнітне поле
демонструє певні риси подібності до
ідеального суцільного середовища,
поведінка якого описується рівняннями,
що зводяться до законів збереження
маси, імпульсу, енергії і моменту
імпульсу.
б) Інтегральна форма закону збереження енергії
Нехай
заряджені частинки рухаються всередині
деякого об’єму
![]() ,
який охоплюється поверхнею
,
який охоплюється поверхнею
![]() .
Заінтегруємо ліву і праву частини
рівняння (14.6) по об’єму
.
Заінтегруємо ліву і праву частини
рівняння (14.6) по об’єму
![]() :
:
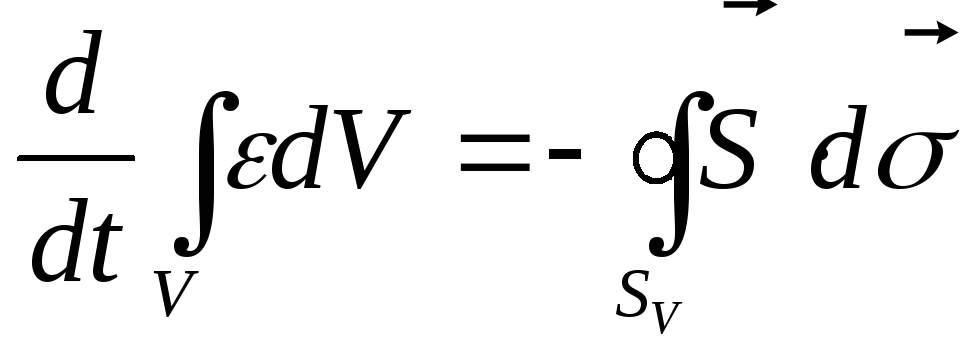 .
(14.10)
.
(14.10)
Скориставшись теоремою Гауса-Остроградського, об’ємний інтеграл від дивергенції було перетворено в поверхневий. Неважко зрозуміти, що
![]()
і рівнянню (14.10) можна надати вигляд:
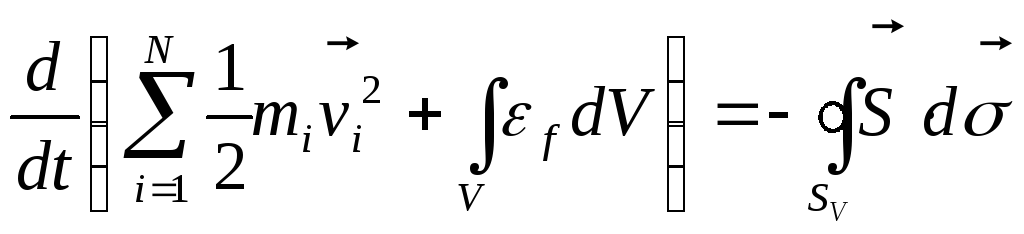 .
(14.11)
Оскільки заряджені
частинки, за умовою, залишаються всередині
об
.
(14.11)
Оскільки заряджені
частинки, за умовою, залишаються всередині
об
![]() ,
,
то зміна сумарної енергії частинок + поле є обумовленою тільки відтоком або надходженням енергії електромагнітного поля через поверхню, яка охоплює систему. Якби енергія системи частинки + поле не зберігалась, до рівняння (4.11) повинні були б входити об’ємні джерела поповнення або стоку енергії системи.
Якщо
![]() ,
то
,
то
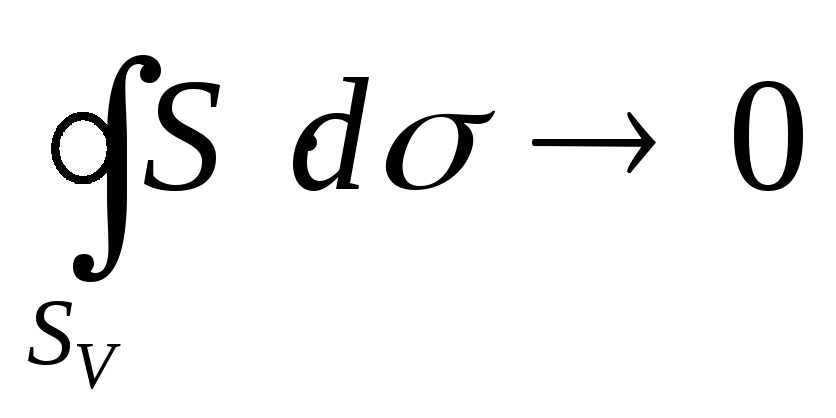 .
Дійсно, електромагнітне поле компактної
системи зарядів на великих відстанях
від неї є сумою 1) квазістатичних
складових:
.
Дійсно, електромагнітне поле компактної
системи зарядів на великих відстанях
від неї є сумою 1) квазістатичних
складових:
![]() і 2) складових, які описують поле
випромінювання:
і 2) складових, які описують поле
випромінювання:
![]() .
В першому випадку
.
В першому випадку
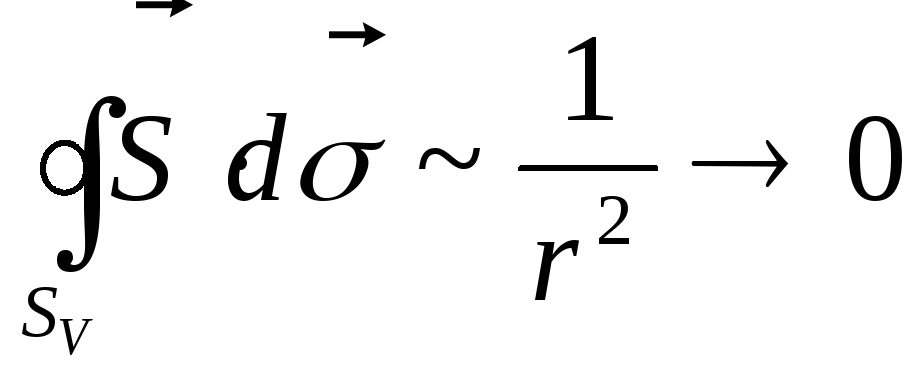 ,
оскільки
,
оскільки
![]() ,
а
,
а
![]() .
В другому випадку враховуємо, що хвильовий
фронт розповсюджується з кінцевою
швидкістю
.
В другому випадку враховуємо, що хвильовий
фронт розповсюджується з кінцевою
швидкістю
![]() ,
завдяки чому поверхню
,
завдяки чому поверхню
![]() завжди
можна вибрати за його межами. Відповідний
поверхневий внесок буде строго дорівнювати
нулю. Таким чином,
завжди
можна вибрати за його межами. Відповідний
поверхневий внесок буде строго дорівнювати
нулю. Таким чином,
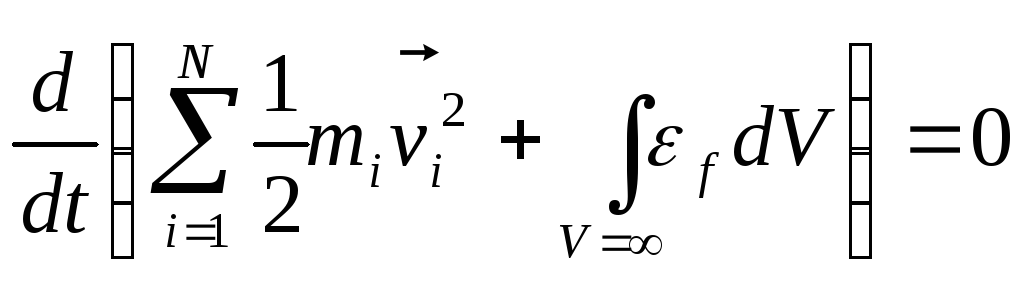 ,
,
або
![]() ,
(14.12)
,
(14.12)
де
![]() - константа розмірності енергії. Це і є
остаточна математична форма закону
збереження енергії для замкнутої системи
заряджені частинки + електромагнітне
поле.
- константа розмірності енергії. Це і є
остаточна математична форма закону
збереження енергії для замкнутої системи
заряджені частинки + електромагнітне
поле.
в) Енергія електростатичного і магнітостатичного полів
Розглянемо різні форми для енергії сумарного електростатичного поля. Згідно (14.12) і (14.6) енергія електричного поля, утвореного нерухомими зарядженими частинками, дорівнює:
![]() .
(14.13)
.
(14.13)
Оскільки
![]() ,
то
,
то
![]() .
(14.14)
.
(14.14)
Скориставшись тепер перетворенням Лежандра:
![]()
і теоремою Гауса-Остроградського, знаходимо:
![]() .
(14.15)
.
(14.15)
Способом, використаним вище, неважко впевнитись, що
![]() .
.
Таким чином, формула (14.13) для енергії електричного поля переходить у
![]() .
(14.16)
.
(14.16)
Якщо всередині системи є заряджені поверхні, формули (14.15) і, як наслідок, (14.16) ускладнюються. Дійсно, в цьому випадку
![]() .
.
Приймаючи
до уваги граничні умови:
![]() ,
для енергії електричного поля отримуємо:
,
для енергії електричного поля отримуємо:
![]() .
(14.17)
.
(14.17)
Розрахуємо
енергію однорідно зарядженої кулі
радіуса
![]() .
Скористаємось найбільш підходящою для
цієї мети формулою (14.16):
.
Скористаємось найбільш підходящою для
цієї мети формулою (14.16):
![]() .
.
Оскільки
![]() ,
то
,
то
![]() ,
(14.18)
,
(14.18)
де
![]() - заряд кулі. Куля, заряд якої утримується
постійним, а радіус прямує до нуля, може
служити моделлю точкового заряду.
Енергія електричного поля точкового
заряду, таким чином, є нескінченою. Такий
самий висновок можна зробити, якщо
точковий заряд моделювати зарядженою
сферою, радіус якої прямує до нуля при
фіксованій величині поверхневого
заряду.
- заряд кулі. Куля, заряд якої утримується
постійним, а радіус прямує до нуля, може
служити моделлю точкового заряду.
Енергія електричного поля точкового
заряду, таким чином, є нескінченою. Такий
самий висновок можна зробити, якщо
точковий заряд моделювати зарядженою
сферою, радіус якої прямує до нуля при
фіксованій величині поверхневого
заряду.
Якщо електричне поле утворюється сукупністю заряджених куль, то енергію їх електричного поля слід обчислювати за формулою:
![]() .
.
Потенціал
всередині
![]() ї
кулі доцільно представляти у вигляді:
ї
кулі доцільно представляти у вигляді:
![]() ,
,
де
![]() - складова потенціалу, утворена власним
розподілом заряду всередині
- складова потенціалу, утворена власним
розподілом заряду всередині
![]() ї
частинки, а
ї
частинки, а
![]() -
складова потенціалу, обумовлена всіма
іншими зарядами. У згоді з цим
-
складова потенціалу, обумовлена всіма
іншими зарядами. У згоді з цим
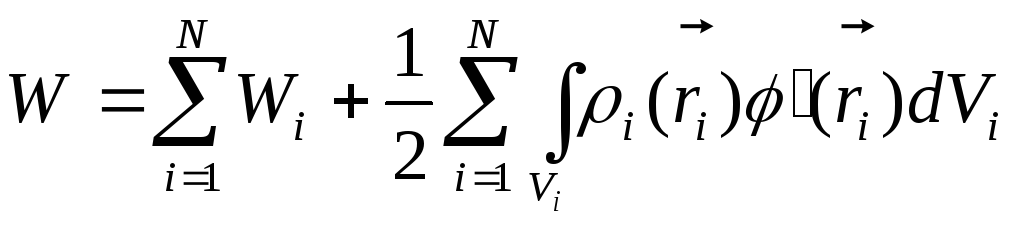 .
(14.19)
.
(14.19)
де
![]() - енергія власного поля
- енергія власного поля
![]() ї
кулі.
ї
кулі.
При переході до сукупності точкових зарядів в формулі (14.19) має смисл залишати тільки енергію взаємодії між зарядами:
![]() ,
(14.20)
,
(14.20)
де
![]() - потенціал, утворений всіма іншими
зарядами в точці розташування
- потенціал, утворений всіма іншими
зарядами в точці розташування
![]() ї
частинки.
ї
частинки.
г) Енергія магнітостатичного поля
Згідно (14.6) енергія магнітостатичного поля визначається рівнянням:
![]() .
(14.21)
.
(14.21)
В багатьох
випадках більш доцільними можуть
виявитись вирази, які можна отримати з
(14.21) за допомогою тотожних перетворень.
Скористаємось для цього стандартним
співвідношенням
![]() .
Тоді (14.21) можна переписати у вигляді:
.
Тоді (14.21) можна переписати у вигляді:
![]() .
.
Відомо, що
![]() .
.
Оскільки
![]() ,
то
,
то
![]() .
.
Враховуючи,
що для токів, зосереджених в компактній
області простору,
![]() при
при
![]() ,
а
,
а
![]() ,
знаходимо, що
,
знаходимо, що
![]() .
Остаточно, для енергії магнітостатичного
поля знаходимо альтернативну формулу:
.
Остаточно, для енергії магнітостатичного
поля знаходимо альтернативну формулу:
![]() .
(14.23)
.
(14.23)
Фактично, інтегрування в ній виконується тільки по області, зайнятій токами.
Якщо
в просторовій області є поверхні з
токами густиною
![]() ,
то формула (14.23) узагальнюється наступним
чином:
,
то формула (14.23) узагальнюється наступним
чином:
![]() .
(14.24)
.
(14.24)
Дійсно, в цьому випадку
![]() ,
,
де, як
і раніше, поверхня
![]() охоплює внутрішню поверхню
охоплює внутрішню поверхню
![]() .
Неважко зрозуміти, що
.
Неважко зрозуміти, що
![]() .
.
Тут
індекси
![]() позначають проекції векторного потенціалу
і напруженості магнітного поля на
взаємно-перпендикулярні орти
позначають проекції векторного потенціалу
і напруженості магнітного поля на
взаємно-перпендикулярні орти
![]() ,
один з яких (
,
один з яких (![]() )
є перпендикулярним до поверхні
)
є перпендикулярним до поверхні
![]() ,
а два інші лежать в дотичній до неї
площині. Нормальні складові векторних
добутків побудовані стандартним чином
з урахуванням відповідності між
індексами: (
,
а два інші лежать в дотичній до неї
площині. Нормальні складові векторних
добутків побудовані стандартним чином
з урахуванням відповідності між
індексами: (![]() )
)
![]() (
(![]() ).
У згоді з граничними умовами (див.
(7.18)):
).
У згоді з граничними умовами (див.
(7.18)):
![]() ,
,
![]() .
.
Підставляючи ці відмінності в попереднє рівняння, знаходимо
![]() .
.
Тут ми
скористались тим, що поверхневий тік
![]() в системі координат (
в системі координат (![]() )
має компоненти (
)
має компоненти (![]() ),
тому комбінація
),
тому комбінація
![]() дорівнює скалярному добутку відповідних
векторів:
дорівнює скалярному добутку відповідних
векторів:
![]() .
Як наслідок,
.
Як наслідок,
![]() ,
,
що повністю виправдовує застосовність формули (14.24).
Якщо токи є лінійними, то (14.23) переходить у формулу:
![]() ,
(14.25)
,
(14.25)
де
![]() є векторний потенціал магнітного поля,
утворений всіма елементами току, крім
є векторний потенціал магнітного поля,
утворений всіма елементами току, крім
![]() .
.
В
найпростішому випадку, коли замкнутий
лінійний тік
![]() (виток току) знаходиться в зовнішньому
магнітному полі, формула (14.25) призводить
до наступного значення його енергії
взаємодії з полем:
(виток току) знаходиться в зовнішньому
магнітному полі, формула (14.25) призводить
до наступного значення його енергії
взаємодії з полем:
![]() .
(14.26)
.
(14.26)
За
допомогою теореми Стокса і співвідношення
![]() вираз (14.26) перетворюється у формулу:
вираз (14.26) перетворюється у формулу:
![]() ,
,
![]() .
(14.27)
.
(14.27)
Її часто
використовують, коли описують поведінку
витка току у зовнішньому полі, і тому
![]() називають силовою функцією.
називають силовою функцією.
