
Для студентов / Лекции / (2)ВЕД / (1)Геометричні властивості векторних полів
.docГеометричні властивості векторного поля
Властивості векторних полів утворюють основу для послідовного опису властивостей електромагнітного поля. В цьому розділі ми розглянемо основні геометричні аспекти опису векторних полів, а також структуру диференціальних рівнянь, які описують їх аналітичні властивості.
а) Основні поняття
З
геометричної точки зору вектор
![]() задається
направленим відрізком прямої. Довжина
цього відрізку є модулем або величиною
вектора і позначається як
задається
направленим відрізком прямої. Довжина
цього відрізку є модулем або величиною
вектора і позначається як
![]() або
або
![]() .
.
За
означенням, векторне поле
![]() визначається
як сукупність векторів
визначається
як сукупність векторів
![]() ,
заданих в кожній точці
,
заданих в кожній точці
![]() просторової області
просторової області
![]() .
.
Просторове
впорядкування векторів в області
![]() описується векторними (силовими) лініями
поля
описується векторними (силовими) лініями
поля
![]() .
За означенням, векторною лінію називають
лінію, в кожній точці якої дотична до
неї співпадає за напрямком з вектором
.
За означенням, векторною лінію називають
лінію, в кожній точці якої дотична до
неї співпадає за напрямком з вектором
![]() ,
заданим в тій же точці. Густина векторних
ліній в околі деякої точки визначається
як число ліній, які проходять через
одиничну площадку, перпендикулярну до
векторної лінії, на якій розташована
обрана точка. Приймається, що густота
векторних ліній є пропорційною модулю
вектора
,
заданим в тій же точці. Густина векторних
ліній в околі деякої точки визначається
як число ліній, які проходять через
одиничну площадку, перпендикулярну до
векторної лінії, на якій розташована
обрана точка. Приймається, що густота
векторних ліній є пропорційною модулю
вектора
![]() ,
заданого в цій точці.
,
заданого в цій точці.
Розрізняють векторні лінії двох типів. До першого з них відносять векторні лінії, які 1) починаються в якійсь точці і прямують до нескінченості; 2) приходять із нескінченості і закінчуються в якійсь точці і 3) починаються в одній точці і закінчуються в другій (див. Рис.1а). До другого типу відносять замкнуті векторні лінії (Рис.1б). Вважається, що лінії, які починаються і закінчуються на нескінченості є замкнутими.


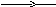
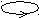
а) б)
Рис.1. Типи векторних ліній.
Приймається, що векторні лінії починаються на позитивних зарядах і закінчуються на негативних зарядах. Кількість ліній, які виходять з заряду або входять до нього, є пропорційною величині заряду. Замкнуті векторні лінії пов’язуються з токами зарядів, точніше, охоплюють токи зарядів. Чим більший тік, тим більшою є густота векторних ліній.
В
багатьох випадках використовується
інша термінологія: кажуть, що векторні
лінії починаються в джерелах, а
закінчуються в стоках поля
![]() .
.
Наочне уявлення про характер векторних ліній і їх зв'язок з джерелами і стоками можна отримати, розглянувши рух води на поверхні річки (Рис.2).
Рис.2. Лінії току води на поверхні річки.
Тут векторні лінії називають лініями току, джерелами ліній току будуть притоки річок або звичайні джерела на дні річки, роль стоків належить канавкам, за допомогою яких вода відводиться з річки. Кругові рухи на поверхні води виникають при наявності в річці якихось перешкод або нерівностей берега.
б) Дивергенція і ротор векторного поля
Ми розрізняємо точкові і розмазані заряди. В останньому випадку розподіл заряду характеризується густиною:
![]() ,
(1.1)
,
(1.1)
де
![]() є
заряд, який попадає в об’єм
є
заряд, який попадає в об’єм
![]() навколо точки
навколо точки
![]() в момент часу
в момент часу
![]() .
У згоді з прийнятою вище домовленістю,
кількість силових ліній
.
У згоді з прийнятою вище домовленістю,
кількість силових ліній
![]() ,
яка виходить за межі об’єму
,
яка виходить за межі об’єму
![]() ,
є пропорційною
,
є пропорційною
![]() .
Тут також бажано перейти до густини
.
Тут також бажано перейти до густини
![]() ,
(1.2)
,
(1.2)
яка за
своїм смислом є локальною мірою
розбіжності векторних ліній поля
![]() .
Міру розбіжності векторних ліній інакше
називають дивергенцією поля
.
Міру розбіжності векторних ліній інакше
називають дивергенцією поля
![]() :
:
![]() .
(1.3)
.
(1.3)
Означенню
дивергенції можна надати дещо іншого
вигляду, якщо величину
![]() пов’язати
з потоком вектора
пов’язати
з потоком вектора
![]() через замкнуту поверхню
через замкнуту поверхню
![]() ,
яка охоплює об’єм
,
яка охоплює об’єм
![]() .
Неважко впевнитись, що
.
Неважко впевнитись, що
![]() ,
(1.4)
,
(1.4)
де
![]() - векторний елемент поверхні,
- векторний елемент поверхні,
![]() є одиничний вектор, який задає орієнтацію
поверхні
є одиничний вектор, який задає орієнтацію
поверхні
![]() .
За звичай, напрямок вектора
.
За звичай, напрямок вектора
![]() відповідає напрямку руху точки зсередини
об’єму зовні. Скалярний добуток під
знаком інтеграла
відповідає напрямку руху точки зсередини
об’єму зовні. Скалярний добуток під
знаком інтеграла
![]() є число векторних ліній, які перетинають
елемент поверхні
є число векторних ліній, які перетинають
елемент поверхні
![]() (тут
(тут
![]() ).
Тобто, інтеграл справа в (1.4) дорівнює
повному числу ліній, які перетинають
поверхню
).
Тобто, інтеграл справа в (1.4) дорівнює
повному числу ліній, які перетинають
поверхню
![]() .
Завдяки цьому формулі (1.3) можна надати
наступного вигляду:
.
Завдяки цьому формулі (1.3) можна надати
наступного вигляду:
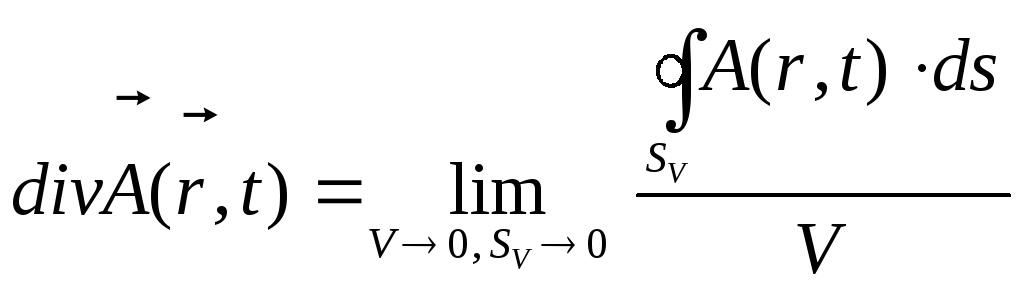 .
(1.5)
.
(1.5)
Оскільки
![]() ,
то
,
то
![]() ,
(1.6)
,
(1.6)
де
![]() - коефіцієнт пропорційності.
- коефіцієнт пропорційності.
Якщо
в точці
![]() знаходиться
точковий заряд скінченої величини, то
знаходиться
точковий заряд скінченої величини, то
![]() також буде скінченою величиною, яка не
залежить від об’єму
також буде скінченою величиною, яка не
залежить від об’єму
![]() .
Тобто
.
Тобто
![]() .
(1.7)
.
(1.7)
Іншими словами, в точці знаходження точкового заряду
![]() .
(1.8)
.
(1.8)
Аналіз
векторних полів із замкнутими векторними
лініями бажано розпочати з векторного
поля швидкостей на поверхні річки. Це
є найпростіший і найбільш наочний
приклад. Круговий рух поверхні води
природно характеризувати кутовою
швидкістю
![]() .
Швидкість води
.
Швидкість води
![]() відносно
центру її обертання на відстані
відносно
центру її обертання на відстані
![]() від нього визначається стандартним
чином:
від нього визначається стандартним
чином:
![]() .
(1.9)
.
(1.9)
Розглядаючи
(1.9) як рівняння відносно кутової швидкості
води, ми можемо знайти його розв’язок
алгебраїчним шляхом, а також звернутись
до обчислення циркуляції вектора
скорості вздовж кола з центром у точці
![]() .
Другим способом знаходимо:
.
Другим способом знаходимо:
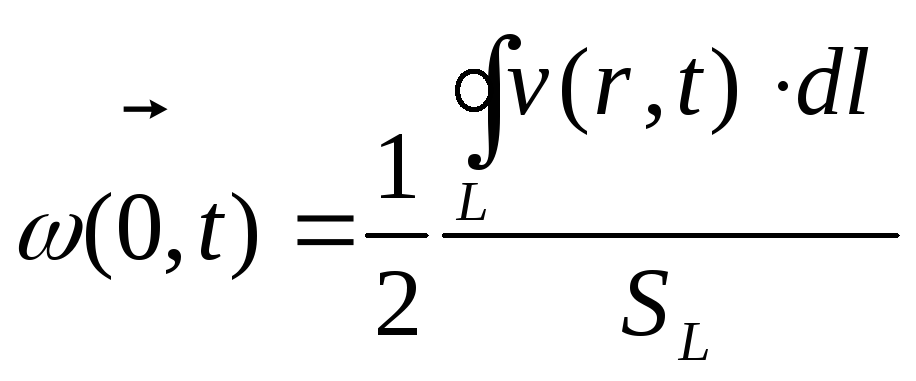 .
(1.10)
.
(1.10)
Тут
![]() - коло радіуса
- коло радіуса
![]() ,
яке лежить у площині, перпендикулярній
до вектора кутової швидкості,
,
яке лежить у площині, перпендикулярній
до вектора кутової швидкості,
![]() -
площа круга, охопленого цим колом.
Векторний диференціал
-
площа круга, охопленого цим колом.
Векторний диференціал
![]() ,
де
,
де
![]() -
довжина елемента кола, а
-
довжина елемента кола, а
![]() -
одиничний орт, дотичний до кола у кожній
його точці. Оскільки
-
одиничний орт, дотичний до кола у кожній
його точці. Оскільки
![]() ,
то циркуляція вектора скорості вздовж
кола дорівнює:
,
то циркуляція вектора скорості вздовж
кола дорівнює:
![]() і
права частина (1.10) в точності переходить
в її ліву частину. Обраний нами спосіб
допускає подальші узагальнення.
і
права частина (1.10) в точності переходить
в її ліву частину. Обраний нами спосіб
допускає подальші узагальнення.
Можна
переконатись, що якщо коло
![]() перетворюється у довільну замкнуту
криву, яка лежить у площині, довільно
орієнтованій відносно вектора кутової
швидкості, то (1.10) узагальнюється
наступним чином:
перетворюється у довільну замкнуту
криву, яка лежить у площині, довільно
орієнтованій відносно вектора кутової
швидкості, то (1.10) узагальнюється
наступним чином:
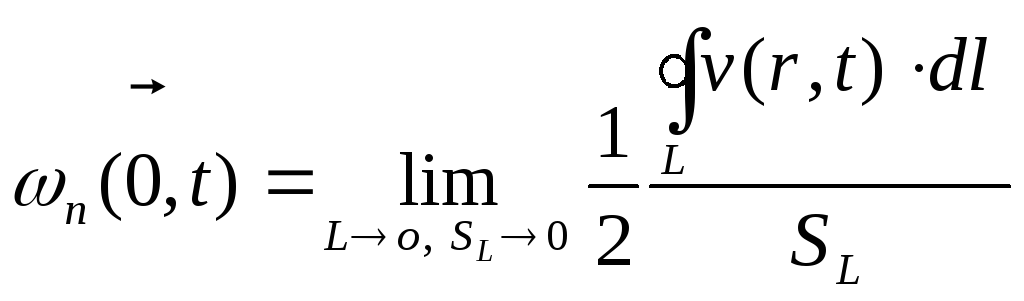 .
(1.11)
.
(1.11)
За
означенням, ротором векторного поля
![]() називають
векторну величину:
називають
векторну величину:
![]() ,
(1.12)
,
(1.12)
яка має смисл міри завихрення поля швидкостей.
Оскільки
векторні лінії поля
![]() можна
завжди розглядати як лінії току поля
швидкостей, то ротор поля
можна
завжди розглядати як лінії току поля
швидкостей, то ротор поля
![]() буде
визначатись цілком аналогічним чином:
буде
визначатись цілком аналогічним чином:
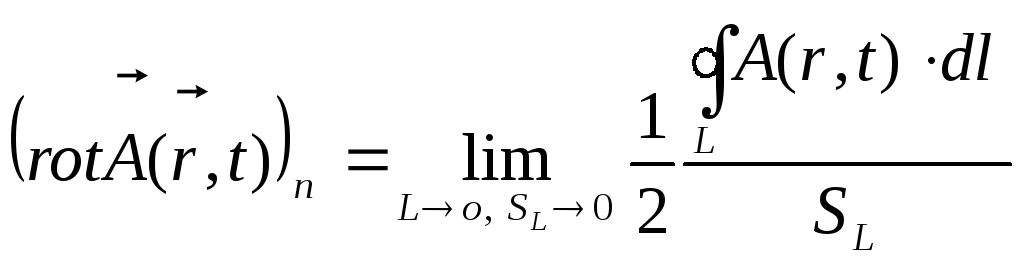 .
(1.13)
.
(1.13)
Інтегральні
означення (1.5) і (1.13) дивергенції і ротора
векторного поля можуть бути використані
для побудови формул, які дозволяють
обчислити
![]() і
і
![]() за
допомогою часткових похідних від
компонентів вектора
за
допомогою часткових похідних від
компонентів вектора
![]() .
Як показано в Розділі …, в ДСК вони
дорівнюють:
.
Як показано в Розділі …, в ДСК вони
дорівнюють:
![]() ,
,
![]() ,
(1.14)
,
(1.14)
де
![]() -
(1.15)
-
(1.15)
оператор набла. Так само обчислюються дивергенція і ротор і в інших системах координат. Зокрема, в циліндричній і сферичній системах координат оператор набла потрібно брати у вигляді:
![]() ,
ЦСК, (1.16)
,
ЦСК, (1.16)
![]() ,
ССК.
(1.17)
,
ССК.
(1.17)
в)
Диференціальні рівняння для визначення
векторного поля
![]()
Для
того, щоб зрозуміти якою інформацією
треба володіти для визначення векторного
поля
![]() ,
звернемось до поля швидкостей на поверхні
води в річці. Розглянемо відрізок річки
довжини
,
звернемось до поля швидкостей на поверхні
води в річці. Розглянемо відрізок річки
довжини
![]() .
Припустимо, що на протязі цієї ділянки
берега річки є прямими і течія цілком
спокійною. Лінії току в цьому випадку
є прямими (див. Рис.3).
.
Припустимо, що на протязі цієї ділянки
берега річки є прямими і течія цілком
спокійною. Лінії току в цьому випадку
є прямими (див. Рис.3).
Рис.3. Лінії току води на поверхні річки за відсутності джерел.
Збурення такого току води відбувається в тих місцях, де річка протікає над джерелом води чи над корягою, яка приводить до закручення потоку. Лінії току на поверхні річки будуть змінюватись і в тому випадку, коли в річку впадатиме струмочок чи вода витікатиме з річки через якийсь відводок. Зазначимо, що зміна поверхневого току води залежить також від його взаємодії з глибинними шарами води, але тут для спрощення ситуації ми не будемо вдаватися в деталі.
Виходячи з цієї картини потоку води в річці ми можемо заключити, що для повного її опису треба знати:
0) картину водотоку в річці без джерел, саме на неї будуть накладатись всі збурення, які вводяться нижче;
1) розташування і інтенсивність (або потужність) джерел поля току води: витоків або стоків, а також тих, що закручують воду, у всіх точках поверхневого шару води. Інакше кажучи, необхідно знати
![]() і
і
![]() для всіх
для всіх
![]() ,
і
,
і
![]() ,
,
де
![]() -
об’єм поверхневого шару на певній
ділянці річки,
-
об’єм поверхневого шару на певній
ділянці річки,
![]() -
початковий для спостереження момент
часу. Ми враховуємо, що потужність джерел
може змінюватись з часом;
-
початковий для спостереження момент
часу. Ми враховуємо, що потужність джерел
може змінюватись з часом;
2) граничні умови, тобто розташування і потужність струмочків, що впадають в річку, і відводків води (і ті і другі розташовані вздовж берега). Крім того треба знати, скільки води протікає через переріз поверхневого шару річки на початку виділеної ділянки і в її кінці. Фактично, це зводиться до того, щоб задати нормальні і тангенціальні складові швидкості води на її поверхні:
![]() і
і
![]() для всіх
для всіх
![]() ,
і
,
і
![]() ,
,
де
![]() -
замкнута лінія, утворена берегами річки,
і лініями, які обмежують ділянку поверхні
річки;
-
замкнута лінія, утворена берегами річки,
і лініями, які обмежують ділянку поверхні
річки;
3) початкові умови, тобто значення
![]() для
всіх
для
всіх
![]() .
.
Виходячи
з подібності векторних ліній для різних
полів, всі ці вимоги зберігаються і для
довільного векторного поля
![]() ,
визначеного в області
,
визначеного в області
![]() ,
яка обмежена поверхнею
,
яка обмежена поверхнею
![]() .
Тобто, треба задати:
.
Тобто, треба задати:
-
потужності джерел
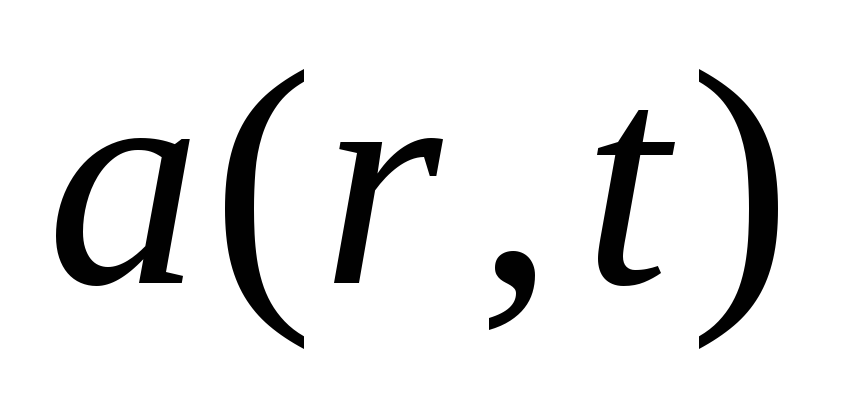 і
і
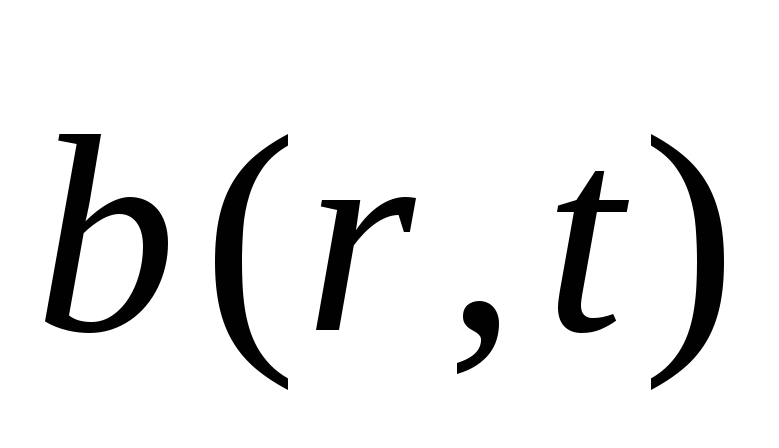 :
:
![]() для
всіх
для
всіх
![]() ,
і
,
і
![]() ,
(1.18)
,
(1.18)
-
граничні умови:
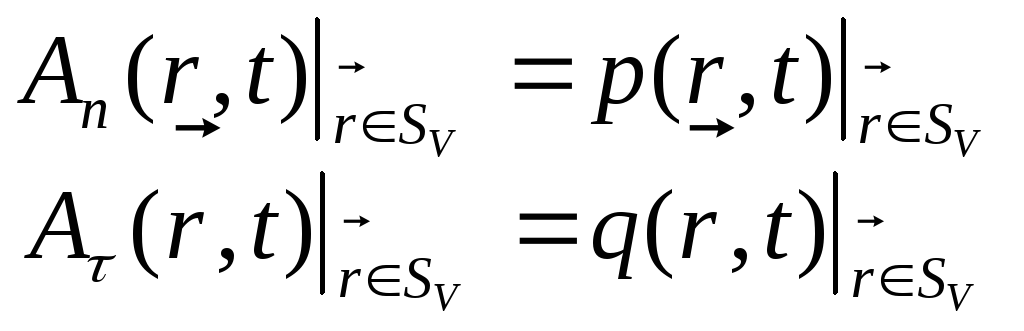 для
всіх
для
всіх
![]() ,
і
,
і
![]() ,
(1.19)
,
(1.19)
-
початкові умови:
![]() для
всіх
для
всіх
![]() .
(1.20)
.
(1.20)
Фактично,
співвідношення (1.18) є диференціальними
рівняннями першого порядку в часткових
похідних для визначення поля
![]() по значенням потужностей його скалярних
і векторних джерел. Граничні і початкові
умови допомагають нам відібрати належний
розв’язок з цілого класу розв’язків.
по значенням потужностей його скалярних
і векторних джерел. Граничні і початкові
умови допомагають нам відібрати належний
розв’язок з цілого класу розв’язків.
г) Загальна структура векторного поля
Завдяки
лінійності рівнянь (1.16), а також у згоді
з картиною ліній току на поверхні річки,
довільне векторне поле
![]() має структуру:
має структуру:
![]() ,
,
де
![]() -
складова
поля, для якої потужності скалярного і
векторного джерел у всіх точках області
-
складова
поля, для якої потужності скалярного і
векторного джерел у всіх точках області
![]() дорівнюють нулю:
дорівнюють нулю:
![]() для
всіх
для
всіх
![]() ,
і
,
і
![]() ,
(1.21)
,
(1.21)
![]() -
потенціальна складова, яка задовольняє
умовам:
-
потенціальна складова, яка задовольняє
умовам:
![]() для
всіх
для
всіх
![]() ,
і
,
і
![]() ,
(1.22)
,
(1.22)
і
![]() - вихрова або соленоїдна складова, яка
описується рівняннями:
- вихрова або соленоїдна складова, яка
описується рівняннями:
![]() для
всіх
для
всіх
![]() ,
і
,
і
![]() .
(1.23)
.
(1.23)
Складова
![]() ,
яку називають також гармонічною
складовою, обумовлена скалярними і
векторними джерелами, які розташовані
за межами області
,
яку називають також гармонічною
складовою, обумовлена скалярними і
векторними джерелами, які розташовані
за межами області
![]() .
Граничні умови, як правило, не розпадаються
на граничні умови для гармонічної,
потенційної і вихрової складової.
.
Граничні умови, як правило, не розпадаються
на граничні умови для гармонічної,
потенційної і вихрової складової.
Для подальшої деталізації структури поля скористаємось наступною обставиною. Якщо
![]() для
всіх
для
всіх
![]() ,
і
,
і
![]() ,
,
то поле
![]() є градієнтом від скалярної функції
(див. ()):
є градієнтом від скалярної функції
(див. ()):
![]() .
.
Тоді
![]() ,
,
де
![]() є оператор Лапласу.
є оператор Лапласу.
Далі, якщо
![]() для
всіх
для
всіх
![]() ,
і
,
і
![]() ,
,
то поле
![]() є ротором від векторної функції (див.
()):
є ротором від векторної функції (див.
()):
![]() .
.
В цьому випадку
![]() .
.
Завжди можна накласти додаткову умову:
![]() ,
,
тоді
![]() .
.
Враховуючи
ці факти, довільне поле
![]() можна
представити у вигляді:
можна
представити у вигляді:
![]() ,
(1.24)
,
(1.24)
де
скалярні
![]() ,
,
![]() і векторний
і векторний
![]() потенціали
задовольняють рівнянням Лапласа і
Пуассона:
потенціали
задовольняють рівнянням Лапласа і
Пуассона:
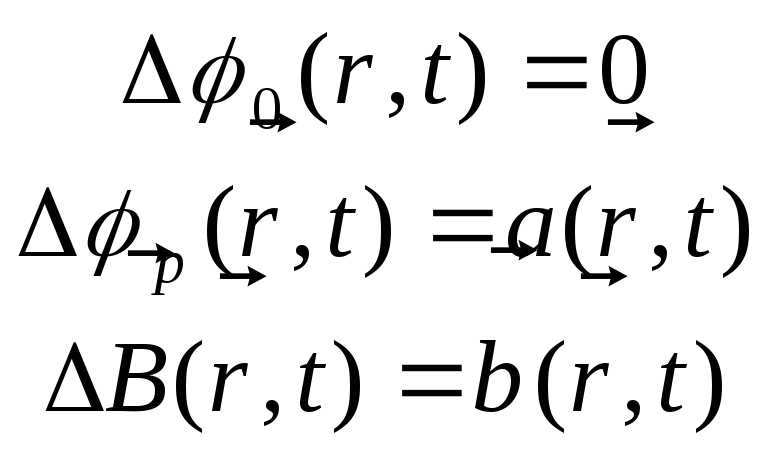 для
всіх
для
всіх
![]() ,
і
,
і
![]() .
(1.25)
.
(1.25)
д) Інтегральні теореми
Важливу
роль у вирішенні багатьох проблем
електродинаміки відіграють інтегральні
теореми, відкриті Гаусом і Остроградським,
а також Стоксом. Теорема Гауса-Остроградського
встановлює зв'язок між об'ємним інтегралом
від дивергенції і потоком векторного
поля
![]() через орієнтовану поверхню
через орієнтовану поверхню
![]() ,
яка охоплює довільний об’єм
,
яка охоплює довільний об’єм
![]() (див. Рис.):
(див. Рис.):
![]()
![]() .
(1.26)
.
(1.26)
Вважається,
що напрямок локальної нормалі до поверхні
![]() відповідає руху точки зсередини зовні.
Зазначимо, що формула (1.26) була отримана
Гаусом і Остроградським незалежно і
майже одночасно.
відповідає руху точки зсередини зовні.
Зазначимо, що формула (1.26) була отримана
Гаусом і Остроградським незалежно і
майже одночасно.
Формула
Стокса має зовсім іншу природу. Вона
встановлює зв'язок між циркуляцією
вектора
![]() вздовж замкнутого контуру
вздовж замкнутого контуру
![]() і потоком ротора векторного поля через
довільну орієнтовану поверхню
і потоком ротора векторного поля через
довільну орієнтовану поверхню
![]() ,
яка спирається на цей контур:
,
яка спирається на цей контур:
![]() .
(1.27)
.
(1.27)
Орієнтація
поверхні
![]() повинна бути узгодженою з позитивним
напрямком обходу контуру
повинна бути узгодженою з позитивним
напрямком обходу контуру
![]() (проти ходу кінця хвилинної стрілки
годинника). Узгодження відбувається за
допомогою правила «буравчика», або
«штопора». Приймається, що напрямок
локальної нормалі до поверхні
(проти ходу кінця хвилинної стрілки
годинника). Узгодження відбувається за
допомогою правила «буравчика», або
«штопора». Приймається, що напрямок
локальної нормалі до поверхні
![]() співпадає з напрямком руху буравчика,
якщо останній обертається протилежно
обертанню хвилинної стрілки годинника
(див. Рис.).
співпадає з напрямком руху буравчика,
якщо останній обертається протилежно
обертанню хвилинної стрілки годинника
(див. Рис.).
Інтегральні
теореми Гауса-Остроградського і Стокса
безпосередньо пов'язані з означеннями
дивергенції (1.5) і ротора (1.11), (1.12)
векторного поля
![]() .
.
Теореми Гауса-Остроградського і Стокса дозволяють встановити також наступні споріднені співвідношення:
![]() (1.28)
(1.28)
і
![]() .
(1.29)
.
(1.29)
Дійсно,
помножимо ліву чистину (1.28) на постійний
вектор
![]() .
Зрозуміло, що його можна внести під знак
інтегралу. Оскільки,
.
Зрозуміло, що його можна внести під знак
інтегралу. Оскільки,
![]() ,
,
то
 .
(1.30)
.
(1.30)
Тут на
другому кроці ми скористались теоремою
Гауса-Остроградського, а потім вектор
![]() винесли з під знаку інтеграла. Рівність
вихідного і кінцевого виразів в (1.30) має
місце при довільному
винесли з під знаку інтеграла. Рівність
вихідного і кінцевого виразів в (1.30) має
місце при довільному
![]() ,
тому можна стверджувати, що інтеграли,
які входять в (1.28), також дорівнюють один
одному.
,
тому можна стверджувати, що інтеграли,
які входять в (1.28), також дорівнюють один
одному.
Такий самий спосіб можна застосувати і для доведення (1.29). Мають місце наступні тотожні перетворення:
![]() .
(1.31)
.
(1.31)
На третьому кроці ми скористались теоремою Стокса. Тепер потрібно згадати, що скалярний добуток двох векторів є комутативним, а змішаний добуток трьох векторів є інваріантним відносно циклічних перестановок. Це дає нам можливість послідовно написати:
![]() .
.
Підставляючи кінцевий результат в (1.31), знаходимо вираз:
![]() ,
,
з якого і випливає (1.29).
e) Невеличкий екскурс в історію
Чи існують векторні лінії в природі? Відповідь на це запитання така ж сама, як і на питання: «Чи існують в природі паралелі і меридіани?». Але на початку 30-х років минулого сторіччя Москва і Ленінград здригались від дискусій на сформульовані запитання. В них вимушені були приймати участь, навіть, видатні радянські фізики І.Є.Тамм, лауреат Нобелівської премії, і Я.І. Френзель. Безумовно, вони роз’яснювали, що ніяких векторних ліній в природі не існує, що їх вводять для більш наочного зображення структури векторних полів. І.Є.Тамм запитував опонентів: «Ну де Ви бачили не Землі темно-сині меридіональні лінії?». Але філософи-більшовики, яким би більше пристало замітати вулиці, були іншої думки. Під бурхливі оплески залу, переповненого вчорашніми активістами комітетів бідноти, професор Міткевич вигукує І.Є Тамму: «Не знаю, якого кольору ваші меридіани, а мій меридіан - червоний». Далі заперечувати було вже зайвим. Можна було б і посміхнутись! Та через кілька місяців Ігор Євгенович і його колеги попали під жахливі жорна НКВС СРСР (Народного Комісаріату Внутрішніх Справ СРСР – радянського гестапо).
