
- •Оглавление
- •Раздел 1. Линейная оптимизация 6
- •Раздел 2. Методы решения задачи многокритериальной оптимизации 19
- •Раздел 3. Применение matlab и excel для решения задач многокритериальной оптимизации 41
- •Перечень условных обозначений, символов, сокращений и терминов
- •Введение
- •Раздел 1. Линейная оптимизация
- •1.1. Линейное программирование
- •1.2. Многокритериальная оптимизация
- •Раздел 2. Методы решения задачи многокритериальной оптимизации
- •2.1. Метод последовательных уступок
- •2.2. Метод главного критерия
- •2.3. Метод свертывания критериев
- •Раздел 3. Применение matlab и excel для решения задач многокритериальной оптимизации
- •3.1. Пакет matlab
- •3.1.2. Toolboxes и его виды
- •3.1.3. Реализация генетического алгоритма в пакете matlab
- •3.2. Решения экономическую модель с помощью инструмента matlab
- •3.3. Решения экономическую задачу многокритериальной оптимизации с помощью ms Excel
- •3.3.1. Метод последовательных уступок
- •3.3.2. Метод главного критерия
- •3.3.3. Метод свертка критериев
- •3.4. Анализ полученных результатов
- •Заключение
- •Список использованной литературы
- •Приложения
2.2. Метод главного критерия
Этот метод предполагает сведения задачи многокритериальной оптимизации к однокритериальной оптимизации . Для этого выбираем один из рассматриваемых критериев в качестве главного критерия, а остальные преобразовываются в ограничения [21].
В качестве главного критерия в различных областях часто выбирают:
1. Себестоимость
2. Объем производства
3. Производительность
4. Ресурсоемкость (металлоемкость, энергоемкость,...)
5. Сроки выполнения работы и др.
Задача оптимизации в этом
случае, можно сформулировать следующим
образом. Вначале нужно задать главный
критерий
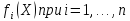 .
После этого, для остальных критериев
вводится система контрольных показателей.
Т.е. для каждого критерия нужно задать,
что он не должен превышать или быть
меньшим, чем некоторое заданное величина
. После этого решается задача
однокритериальной условной оптимизации,
где
.
После этого, для остальных критериев
вводится система контрольных показателей.
Т.е. для каждого критерия нужно задать,
что он не должен превышать или быть
меньшим, чем некоторое заданное величина
. После этого решается задача
однокритериальной условной оптимизации,
где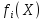 стремится к максимуму или минимуму, при
условиях, что каждый частный критерий,
кроме главного критерия будет больше
или равен чем заданное контрольное
значения,
стремится к максимуму или минимуму, при
условиях, что каждый частный критерий,
кроме главного критерия будет больше
или равен чем заданное контрольное
значения,
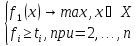 (2.6)
(2.6)
При этом все значении Х должны принадлежать рассматриваемому допустимому множеству. Наиболее часто этот способ употребляется в инженерной практике.
Преимущества метода главного критерия относятся простота интерпретации результатов, отсутствия высоких требований к математической подготовке экспертов, программному обеспечению и вычислительным средствам [51]. После того, как мы сведем задачу многокритериальной оптимизации к задаче однокритериальной оптимизации, мы получаем возможность использовать стандартные программные средства, в частности, такие как поиск решения в Microsoft Excel.
К основным недостатком метода относятся:
1) чрезмерное упрощение структуры задач;
2) не всегда можно выделить ярко выраженный главный критерий, иногда это сделать трудно или вообще нельзя;
3) возможность потери эффекта совокупного влияния нескольких второстепенных критериев;
4) ограничения для остальных критериев должны быть обоснованными, а не взяты кое-как;
5) возможность получения неэффективных решений;
6) даже если есть критерий, который гораздо важнее любого другого, то не факт, что в сумме остальные критерии не окажутся весьма значимыми. Особо ярко это может проявляться в задачах, где n велико [21,25,30,33,46].
В методе главного критерия, если задача имеет единственное допустимое решение, то оно является эффективным по Парето. Если же задача имеет более чем одно допустимое решение, то множество этих решений содержит эффективные по Парето решения [37,45,48,51]. Но оно также может содержать и слабо эффективные решения.
В связи с этим процедура поиска решения в общем случае включает два этапа:
1) нахождение множества допустимых решений;
2) выбор некоторого эффективного по Парето решения.
На практике, критерии очень часто имеют различные масштабы и шкал измерения, и тогда возникает необходимость нормировки этих критериев.
Нормировка критериев
Для приведения критериев к сопоставимому виду и обеспечения их эквивалентности используется нормировка:
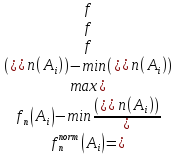 (2.7)
(2.7)
при
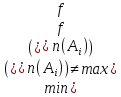 (2.8)
(2.8)
От значения критерия отнимаем
минимальное значение этого критерия и
делим полученную разность на разность
между максимальным и минимальным
значениями этого критерия [51]. Предполагается
при этом, что минимальное и максимальное
значение не совпадают. При такой
нормировке, все нормированные значение
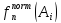 будут лежать в интервале [0;1].
будут лежать в интервале [0;1].
Рассмотрим в качестве
примера такую задачу, предполагается,
что необходимо организовать рекламную
компанию по продвижению нового товара.
Для этого могут быть использованы
альтернативы
 .
Критерии оптимальности - минимум затрат
на рекламу, максимум доли рынка и объема
продаж в течении заданного периода
времени.
.
Критерии оптимальности - минимум затрат
на рекламу, максимум доли рынка и объема
продаж в течении заданного периода
времени.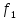 - реклама,
- реклама,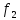 - доля рынка,
- доля рынка,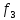 - объем продаж.
- объем продаж.
Исходные данные записываются таким образом:
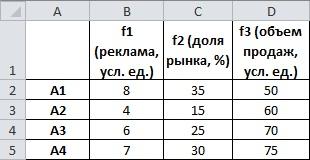 рис.2.8.
Таблица исходных данных
рис.2.8.
Таблица исходных данных
Прежде чем решить задачу,
нужно провести нормировку критериев.
В качестве главного критерия берем
критерию
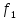 -
затраты за рекламу, а критерия
-
затраты за рекламу, а критерия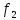 и
и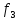 превратим
в ограничения. Поэтому для нормировки
мы можем ограничиться только критериями
превратим
в ограничения. Поэтому для нормировки
мы можем ограничиться только критериями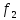 и
и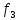 .
Для второго критерия, минимальное
значение будет 15, а максимальное – 35.
Для третьего соответственно 50 и 75. В
качестве примера, можно посчитать
нормированное значение второго критерия
для первой альтернативы:
.
Для второго критерия, минимальное
значение будет 15, а максимальное – 35.
Для третьего соответственно 50 и 75. В
качестве примера, можно посчитать
нормированное значение второго критерия
для первой альтернативы:
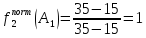
Можно зафиксировать
постоянные значения, т.е. это максимумы
и минимумы у второго и третьего критерия,
затем воспользоваться автозаполнением
для быстроты работы. В результате получим
вот такую таблицу, значения критерия
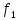 остаются такими же, как были. А значения
критериев
остаются такими же, как были. А значения
критериев и
и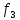 мы
переводим в относительные величины.
мы
переводим в относительные величины.
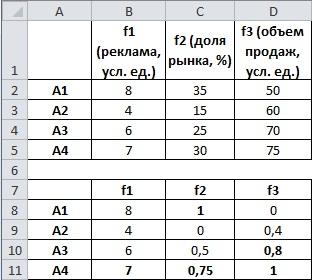
рис.2.9. Нормировка критериев
Выберем такое ограничение,
что частные критерия
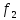 и
и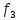 должны
быть не меньше 0,7 умноженное на максимальное
значение этих критериев:
должны
быть не меньше 0,7 умноженное на максимальное
значение этих критериев: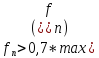 .
.
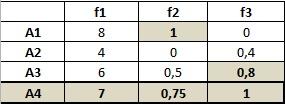
рис. 2.10. Окончательный результат решения по методу главного критерия
Тогда этим ограничениям
для критерия
 удовлетворяет альтернативы
удовлетворяет альтернативы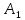 и
и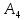 .
А для критерия
.
А для критерия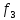 альтернативы
альтернативы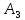 и
и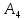 .
Единственная альтернатива, которая
одновременно удовлетворяет ограничением
по критерию
.
Единственная альтернатива, которая
одновременно удовлетворяет ограничением
по критерию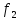 и
по критерию
и
по критерию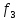 это
альтернатива
это
альтернатива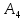 ,
которая в данном случае и выбирается в
качестве оптимального решения.
,
которая в данном случае и выбирается в
качестве оптимального решения.
Для сравнения, возьмем в
качестве ограничение 0,8 умноженное на
максимальное значение критериев
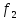 и
и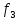 :
: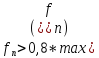 .
Новым ограничением, для критерия
.
Новым ограничением, для критерия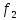 удовлетворяет только альтернатива
удовлетворяет только альтернатива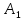 ,
а для критерия
,
а для критерия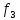 удовлетворяет
альтернативы
удовлетворяет
альтернативы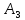 и
и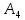 .
Мы не имеем ни одной альтернативы,
которая бы одновременно удовлетворяла
ограничением по критерию
.
Мы не имеем ни одной альтернативы,
которая бы одновременно удовлетворяла
ограничением по критерию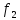 и
по критерию
и
по критерию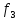 .
Таким образом, множество решения будет
пустое, т.е. мы не можем выбрать оптимальное
решение при таких ограничениях.
.
Таким образом, множество решения будет
пустое, т.е. мы не можем выбрать оптимальное
решение при таких ограничениях.
