4.3.2. Модель постепенного отказа с учетом рассеивания начальных

значений выходных параметров объекта

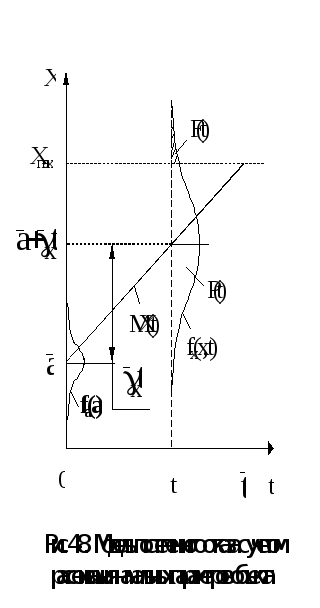
Более полная модель постепенного отказа объекта учитывает и начальное рассеивание значений выходного параметра в момент времени (наработки) t = 0 (рис. 4.8). В общем случае линейный закон изменения выходного параметра объекта имеет вид

, (4.18)

где A = X(0) - начальное значение выходного параметра объекта, которое является непрерывной случайной величиной (случайный характер величины A обусловлен погрешностями изготовления и влиянием быстропротекающих процессов).

Для случайной величины A можно принять нормальный закон распределения с функцией плотности

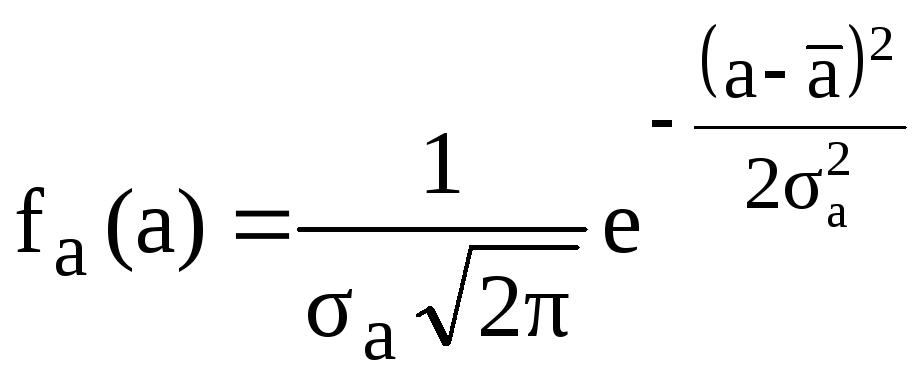, (4.19)

где - математическое ожидание случайной величиныA; _a - среднее квадратическое отклонение случайной величины A.

Случайная величина ₁ - наработка до отказа - является детерминированной функцией двух случайных аргументов A и _x (_x - скорость изменения выходного параметра объекта, которая является случайной величиной, распределенной по нормальному закону (4.6))

.

Непосредственное отыскание закона распределения случайной величины ₁ затруднено, так как функция ₁ в общем случае не является монотонной, поэтому несколько изменим подход к анализу модели и рассмотрим закон распределения выходного параметра объекта X в какой-то текущий момент времени (наработки) t. На основе этого распределения определим вероятность безотказной работы объекта P(t) , определение которой собственно и является целью анализа модели отказа.

Из теории вероятностей известно, что линейная функция (4.18) двух независимых случайных величин, распределенных по нормальному закону, также имеет нормальное распределение с параметрами

- математическое ожидание ;

- дисперсия .

Функция плотности распределения выходного параметра объекта X в момент времени (наработки) t

.

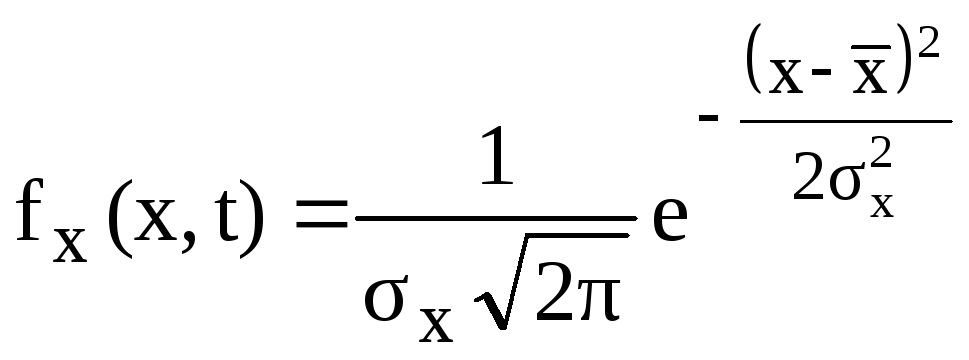Вероятность безотказной работы объекта в рассматриваемый момент времени (наработки) t равна вероятности того, что значение выходного параметра X объекта в этот момент не выйдет за предел X_max

.

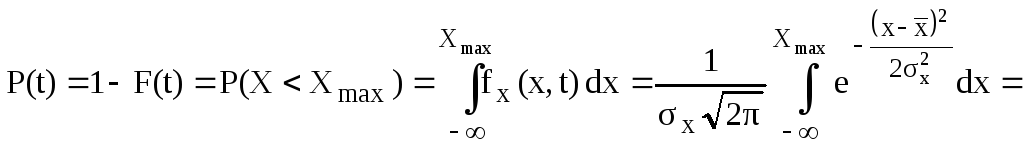
Произведя замену переменной (), получаем:

.

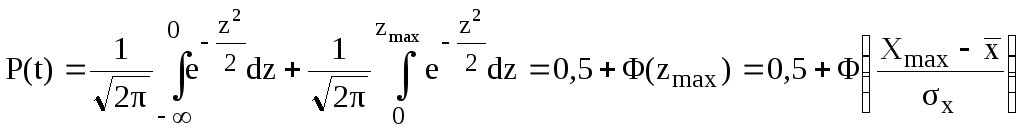Подставив в последнее равенство параметры распределения и, получим:

. (4.20)

Эта формула является более общей по сравнению с формулой (4.17) предыдущего раздела, так как формула (4.17) получается из (4.20) при и.

Частные случаи рассматриваемой модели:

1. Рассеивание процесса X(t) во времени мало (_0; ).

В этом случае наработка объекта до отказа ₁ распределена по нормальному закону, который полностью определяется параметрами закона распределения начального значения выходного параметра A и средней скоростью изменения выходного параметра . Вероятность безотказной работы

,

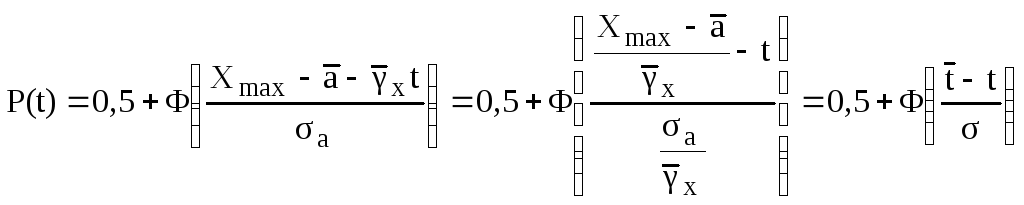где - средняя наработка до отказа; - среднее квадратическое отклонение наработки до отказа.

Функция плотности распределения случайной величины ₁ - наработки объекта до отказа:

, т.е. нормальное распределение.

2. Изменение выходного параметра X на рассматриваемом интервале времени (наработки) (0, t) не наблюдается (накопленные повреждения не приводят к изменению выходного параметра), но начальное рассеивание велико.

В этом случае F(t) оценивает вероятность получения дефектного изделия, которое изначально неработоспособно, а P(t) - вероятность получения годного изделия, которое со 100%-ной вероятностью будет работоспособно на рассматриваемом интервале:

. (4.21)

3. Пример. Пусть выходным параметром X является точность позиционирования стола фрезерного станка с ЧПУ (рис.4.9). Установлен симметричный допуск на значение выходного параметра X:

X_min X X_max – объект работоспособен;

X < X_min или X > X_max – объект неработоспособен.

Средняя скорость изменения выходного параметра , но, т.е. влияние повреждающих процессов проявляется лишь в увеличении со временем дисперсии выходного параметра без смещения центра группирования(износ обеих сторон профиля ходового винта механизма подачи станка равномерен).

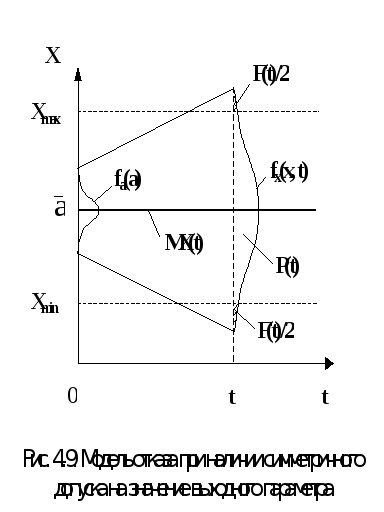
Вероятность безотказной работы для рассматриваемой модели отказа

. (4.22)

В каждый момент времени (наработки) t закон распределения выходного параметра X(t) нормальный с параметрами

;

.