Ниже представлены тригонометрические формулы, по которым были проведены вычисления:

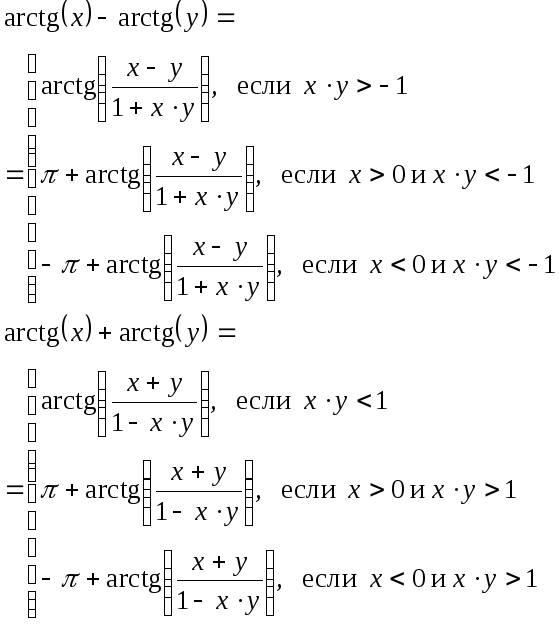
Методика коррекции системы в ВЧ диапазоне в данном случае и в случае метода желаемых ЛАЧХ сводится к тому, что частоты сопряжения ЛАЧХ РС выбираются совпадающими с частотами сопряжения ЛАЧХ ОУ, а наклон асимптот ЛАЧХ РС берется параллельным асимптотам ОУ. Это соответствует тому, что корректирующих звеньев с частотами сопряжения больше, чем в корректирующее устройство не вводится.

Пример.

Пусть ОУ задан следующей передаточной функцией:

.

Пусть критическим входным воздействием на систему является линейная функция времени: . Пусть при отработке критического воздействия необходимая точность не хуже (). Пусть система должна обеспечить время регулирования .

Строим ЛАЧХ ОУ по теории, изложенной в курсе ТАУ.

ПЗ
ДЗ1
КЗ
КЗ		;			.

Строим ЛАЧХ и ЛФЧХ ОУ:

Рисунок 20.

Рассчитаем коэффициент передачи РС:

Для корректирующего устройства:

Определим порядок астатизма КУ(с помощью формулы (17))

, следовательно первый порядок астатизма.

Таким образом получаем ПФ КУ: , и ПФ РС с КУ:

Строим лачх рс с ку:

ИЗ
ДЗ1
КЗ
КЗ		;			.

Рисунок 21.

Исходя из астатизма первого порядка системы и степени ХП, равной пяти, определяем запасы устойчивости по фазе и амплитуде (минимально допустимые):

Определяя запасы устойчивости графически, видим, что они не удовлетворяют заданным.

Так как запасы по фазе меньше предельно допустимых, делаем вывод о необходимости среднечастотной коррекции.

По графику определяем необходимую амплитуду фазовой коррекции:

Выбираем параметры АФО звена для поднятия ЛФЧХ на .

Количество звеньев АФО коррекции:

.

Величина единичной фазовой коррекции:

По графику ( - в радианах), находим , при котором обеспечивается фазовая коррекция на : .

Рассчитаем постоянную времени коррекции:

.

Выберем равным .

Запишем найденное звено АФО коррекции:

Частотная коррекция с использованием АФИ звеньев второго порядка.

Рассмотренные АФИ звенья первого порядка не исчерпывают все возможности коррекции, так как позволяют проектировщику оперировать только действительными корнями числителя и знаменателя КУ. В большинстве стандартных ситуаций этого оказывается достаточно, однако в ряде случаев использование таких звеньев (особенно АФО) приводит к противоречию. Поднимая фазу РС в области частоты среза, оно одновременно поворачивает в положительную сторону ЛАЧХ в этой же части. При большой глубине коррекции этот поворот может привести к тому, что ЛАЧХ в зоне частоты среза будет идти с нулевым или даже положительным наклоном. В результате возникают трудности с обеспечением запаса по модулю, а динамика системы сильно искажается.

Рисунок 22.

ЛАЧХ в области частоты среза должна быть гладкой (без всяких переломов). В случае изломов ПП будет иметь вид:

Рисунок 23.

Можно использовать АФИ звенья второго порядка: как и в случае со звеньями первого порядка, у них должен быть единичный коэффициент передачи. Это будет статическое звено:

.

(23)

При этом возможны четыре ситуации:

1. - корни полинома действительные, полиномы распадаются, следовательно, АФИ звено первого порядка.

2. - в знаменателе комплексные корни.

3. - в числителе комплексные корни.

4. - оба полинома имеют комплексно-сопряженные корни.

Относительно постоянных времени имеется три варианта:

1. - АФО звено первого порядка;

2. - при условии - ни АФО звено, ни АФЗ;

3. - АФЗ звено второго порядка;

При использовании звено второго порядка как АФО, так и АФЗ звеньев, можно использовать дополнительную зависимость формы амплитуды и фазовой характеристики от показателя колебательности . АФО звено имеет асимптотическую ЛАЧХ:

Рисунок 24.

Чем меньше , тем ближе всплеск ЛФЧХ к начальной точке коррекции – точке, где ЛАЧХ начинает подниматься.

В рассмотренном варианте частотной коррекции за счет уменьшения достигается несколько эффектов:

• центр фазовой коррекции смещается к началу диапазона частотной коррекции, что уменьшает влияние поворота асимптоты ЛАЧХ РС на ее величину в районе ;

• импульс фазовой коррекции становится затянутым в сторону высших частот, что затягивает импульс подъема ЛАЧХ РС над ординатой «», увеличивает и облегчает реализацию запаса устойчивости по модулю;

• отрицательный амплитудный всплеск в зоне может оказать положительный эффект для компенсации подъема ЛАЧХ при применении АФО - коррекции.

Аналогично при использовании АФЗ звеньев второго порядка, варьируя не только соотношением , но и , можно добиться нужных эффектов частотной коррекции. Устройства, подобные АФИ звеньям второго порядка используются не только для коррекции ЗС, но и при решении других задач.