10.3 Примеры решения задач

Задача 10.3.1. При градуировке измерительного преобразователя с линейной функцией преобразования получены значения экспериментальных данных, представленные в таблице 10.1. Определите методом средних и МНК аналитические модели градуировочной характеристики, сравните с помощью дисперсии точность этих моделей и проверьте их адекватность, если известно, что дисперсия шума при измерении отклика S_ш²=18,36.

Таблица 10.1 – Экспериментальная градуировочная характеристика

Входное воздействие Q	5	10	20	25	30	35	40	45	50	55	60	65
Отклик преобразователя Х	12	26	45	58	69	74	86	98	110	118	127	140

Решение.

Линейная функция преобразования имеет вид:

Х = а + bQ (10.29)

По методу средних образуем две группы начальных уравнений вида:

Х_i – a – bQ_i = _i (10.30)

В каждой группе складываем их почленно и приравниваем к 0:

и = 0 (10.31)

12 – а – b5 = 86 –а – b40 =

26 – а – b10 = 98 –а – b45 =

45 – а – b20 = 110 –а – b50 =

58 – а – b25 = 118 –а – b55 =

69 – а – b30 = 127 –а – b60 =

74 – а – b35 = 140 –а – b65 =

284 – 6а – 125b = 0 679 – 6а – 315b = 0

Решаем систему нормальных уравнений относительно а и в:

(10.32)

-395 + 190в=0

Модель 1 функции преобразования:

Х=4,02+2,079Q (10.33)

По МНК, используя формулы (10.11) и (10.12), определяем параметры модели:

Модель 2 функции преобразования:

Х=3,829+2,084Q. (10.34)

Рассчитываем для каждой модели СКО по формуле (10.14):

- для модели 1

- для модели 2

42

СКО модели 2, определенной по МНК, меньше. Следовательно, можно сказать, что эта модель более точная.

Проверить адекватность моделей можно по критерию Фишера, сравнив дисперсии модели и отклика Х. Модель адекватна, если выполняется неравенство.

<, (10.35)

где S₀ ² – дисперсия отклика;

F_f1,f2q – коэффициент Фишера для уровня значимости q и числа степеней свободы ,.

где N – число опытов;

d – число неизвестных.

Коэффициент Фишера для уровня значимости q=0,05 и числа степеней свободы(приложение К):

.

Дисперсия отклика (10.36):

Для модели 1:

Для модели 2:

.

Оба вычисленных отношения дисперсий не превышают табличного значения коэффициента Фишера. Следовательно, обе модели адекватны.

Задача 10.3.2. В таблице 10.2 представлены результаты контроля времени при определенной температуре в технологическом процессе изготовления лакокрасочных изделий. Оцените качество работы смен и стационарность технологического процесса.

Таблица 10.2 – Результаты контроля технологического процесса.

№ партии изделия	Температура, 0С
	90	120	150	180	210
	Время от начала технологического процесса, ч
1	2,1	11,4	17,8	26,3	32,2
2	2,3	11,7	17,5	25,9	31,7
3	2,5	10,9	17,2	26,4	32,0
4	2,0	11,3	17,4	26,1	32,4
5	1,9	11,5	17,0	26,6	31,9

Решение.

Так как длительность технологического процесса 32 часа, а продолжительность рабочей смены 8 часов, то смены не совпадают со стадиями процесса. Поэтому о согласованности работы различных смен можно судить по рассеянию длительности в контрольных точках процесса.

Рассчитываем для каждого уровня температуры средние арифметические значения времени (3.17) и дисперсию (3.14):

Вносит ли в технологический процесс существенное различие работа смен можно определить по однородности дисперсий. Полагаем, что процесс подчиняется нормальному закону. Для оценки значимости расхождения средних значений применяем критерий Бартлетта. (раздел 9). Рассчитаем:

- внутригрупповую дисперсию (9.6):

- значения С и Х² (9.8):

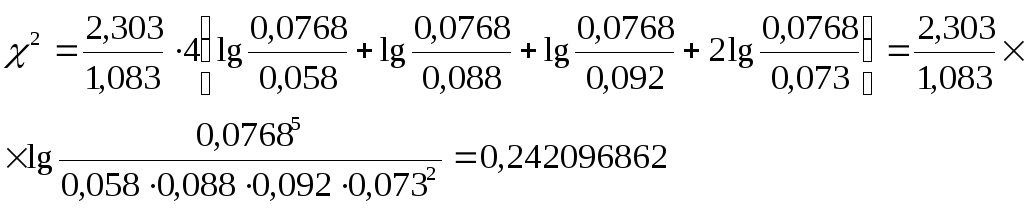
Табличные значения _q² для уровня значимости q = 0,05 и числа степени свободы (приложение Е):

Так как <, то различие дисперсий незначительно, т.е. существенных отличий в работе смен не наблюдается. Можно предположить, что процесс близок к стационарному. Проверим эту гипотезу поG-критерию. Определим расчётное значение G (10.27):

Неравенство (10.27) выполняется:

(приложение Л)

0,239583<0,5441

По дисперсии процесс можно считать стационарным.

Рассчитываем корреляционные функции (10.21):

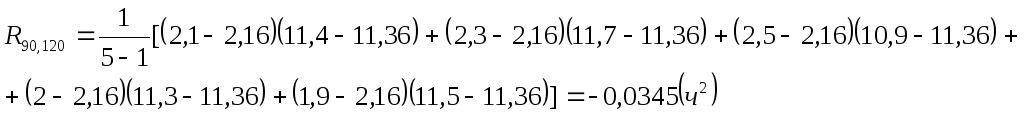
Аналогично вычисляем:

; ;;;

;.

Рассчитываем нормированные корреляционные функции (10.24):

; ;

; ;

; ;

; ;

; .

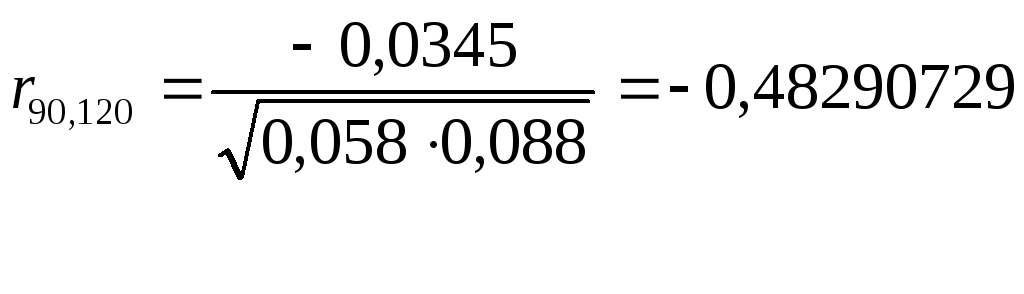Значимость колебаний нормированной корреляционной функции определяем по критерию (10.28):

= -15,1793885

Табличное значение для уровня значимостии числа степеней свободы(приложение Е):=16,00. Следовательно, с вероятностью

Р =1-q = 1- 0,025 = 0,975 процесс можно считать стационарным.