3. Электромагнитные колебания

3.1. Колебательный контур ( - контур). Свободные электромагнитные колебания в контуре без сопротивления.

Колебательный контур (– контур) – электрическая цепь, состоящая из последовательно соединенных конденсатора с емкостью и катушки с индуктивностью .

Рис. 11. Колебательный контур.

В цепи, содержащей индуктивность и емкость, могут возникать электромагнитные колебания.

Свободные электромагнитные колебания – периодические изменения заряда на обкладках конденсатора, напряжения на нем и силы тока в катушке без потребления энергии извне.

Каким же образом в колебательном контуре возникают и поддерживаются электромагнитные колебания?

При подключении обкладок заряженного конденсатора к концам катушки в ней возникает электрический ток, и энергия электрического поля заряженного конденсатора начинает превращаться в энергию магнитного поля катушки индуктивности . Ток в цепи растет, но не мгновенно – этому мешает ЭДС самоиндукции в катушке.

В тот момент, когда конденсатор полностью разрядится и энергия электрического поля станет равной нулю, сила тока в катушке и энергия магнитного поля достигнут максимума. Затем ток начнет убывать, не меняя при этом своего направления. Этот ток поддерживается за счет ЭДС самоиндукции . Начинается перезарядка конденсатора. Напряжение на конденсаторе будет увеличиваться (), а токчерез катушку - уменьшаться. При достижении максимального напряжения ток станет равным 0, и вся энергия контура вновь сосредоточится в конденсаторе.

Теперь процесс повторится, но уже при противоположном направлении тока (рис. 12)_.

Очевидно, что электромагнитные колебания сопровождаются взаимными превращениями энергии электрического и магнитного полей. Так, если в начальный момент времени () полная энергия контурасосредоточена в электрическом поле конденсатора, то через время, равное четверти периода (), полная энергия сосредоточена уже в магнитном поле катушки индуктивностии т. д.

Можно провести аналогию между электрическими колебаниями и механическими колебаниями математического маятника (см. рис. 12).

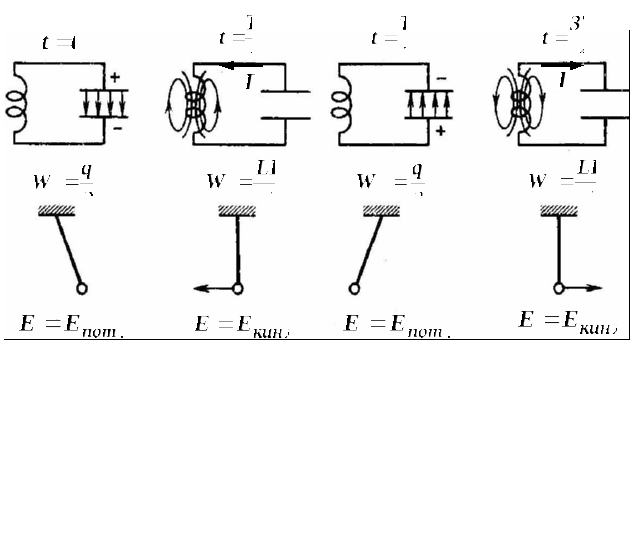
Рис. 12. Сопоставление электромагнитных и механических колебаний.

Здесь – полная энергия колебательного контура, и - амплитудные значения заряда на конденсаторе и силы тока в катушке,- полная энергия маятника.

Если бы не было потерь на джоулево тепло при протекании тока по проводам и катушке, а также потерь энергии на излучение электромагнитных волн, колебания в контуре продолжались бы неограниченно долго. Такие идеализированные колебания и принято называть свободными или собственными колебаниями.

Период (с) свободных электромагнитных колебаний в контуре (формула Томсона):

.

Циклическая частота (рад/с) свободных электромагнитных колебаний в контуре

.

Закон изменения заряда на конденсаторе со временем:

,

где (Кл)– амплитуда заряда на конденсаторе.

График зависимости заряда на обкладке конденсатора от времени показан на рис. 13.

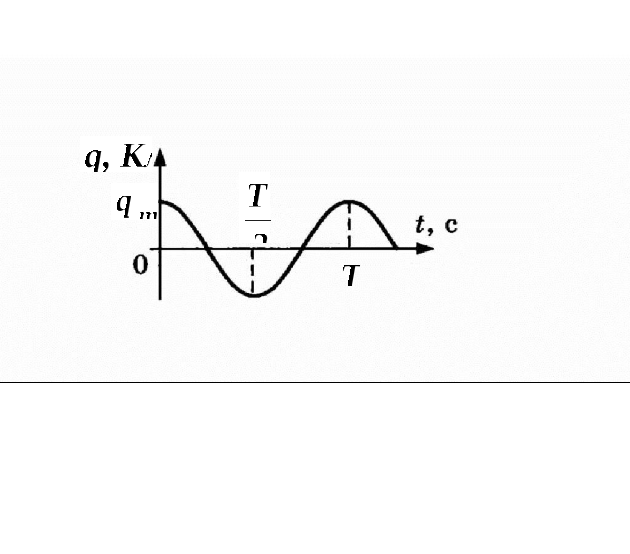
Рис. 13. График зависимости заряда на обкладке конденсатора колебательного контура от времени.

Закон изменения силы тока в катушке со временем:

,

где (А) – амплитуда силы тока в катушке,.

Рассмотренный выше контур, в котором отсутствует электрическое сопротивление, называется идеальным. Всякий реальный контур имеет сопротивление, и колебания заряда и тока в нем из-за энергетических потерь на джоулево тепло будут затухать. Для получения незатухающих колебаний потери энергии в контуре нужно восполнять за счет внешнего источника; такая компенсация возможна, например, при вынужденных колебаниях.