
- •19 Vektor
- •2. Линейные операции над векторами.
- •Свойства линейных операций над векторами.
- •3. Понятие линейной зависимости векторов.
- •4. Понятие о проекциях.
- •Декартова система координат.
- •Связь компонент, проекций, направляющих косинусов и коэффициентов в разложении по базису.
- •Деление отрезка в данном отношении.
- •5. Линейные операции над векторами, заданными своими координатами.
- •5.А. Скалярное произведение векторов.
- •Свойства скалярного произведения.
- •5.Б. Векторное произведение.
- •Векторное произведение двух векторов, заданных своими проекциями.
- •Механический смысл векторного произведения.
- •Свойства векторного произведения векторов.
- •5.В. Смешанное произведение трех векторов.
- •Смешанное произведение векторов, заданных своими координатами.
- •Свойства смешанного произведения.
Декартова система координат.
Ортонормированный
базис образуют взаимно перпендикулярные
векторы
![]() ,
,![]() ,
,![]() единичной длины, т.е.
единичной длины, т.е.
![]() и
и
![]() .
.
Точка
![]() - начало координат
- начало координат![]() .
Прямые, проходящие через начало координат
в направлении векторов
.
Прямые, проходящие через начало координат
в направлении векторов
![]() ,
,![]() ,
,![]() ,
называются осями координат. Векторы
,
называются осями координат. Векторы
![]() ,
,![]() ,
,![]() соответствуют положительному направлению
осей координат:
соответствуют положительному направлению
осей координат:
![]() ,
,![]() ,
,![]() - оси абсцисс, ординат и аппликат.
Плоскости, проходящие через оси координат,
называются координатными плоскостями
- оси абсцисс, ординат и аппликат.
Плоскости, проходящие через оси координат,
называются координатными плоскостями![]() ,
,![]() ,
,![]() (см. рис. 7).
(см. рис. 7).
Определение
16.
Прямоугольной
системой координат
называется совокупность точки (![]() )
и ортонормированного базиса.
)
и ортонормированного базиса.
Определение
17.
Радиус-вектором
произвольной точки
![]() по отношению к точке
по отношению к точке![]() ,
называется вектор
,
называется вектор![]() .
Точке
.
Точке![]() можно сопоставить упорядоченную тройку
чисел (
можно сопоставить упорядоченную тройку
чисел (![]() )
- компоненты ее радиус-вектора:
)
- компоненты ее радиус-вектора:![]() и
и![]() (см. рис. 8).
(см. рис. 8).
О
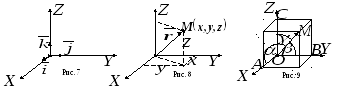 пределение
18.
Компоненты
радиус-вектора точки
пределение
18.
Компоненты
радиус-вектора точки
![]() по отношению к началу координат называют
координатами точки
по отношению к началу координат называют
координатами точки![]() в рассматриваемой системе координат.
в рассматриваемой системе координат.
Координаты вектора совпадают с проекцией вектора на соответствующие оси координат (рис.8):
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]()
Согласно
рис. 9 имеем:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() .
.
 Пусть
вектор
Пусть
вектор
![]() задан координатами крайних точек,
задан координатами крайних точек,![]() и
и![]() (рис. 10).
(рис. 10).
Тогда
![]()
Следовательно,
чтобы определить координаты вектора
по координатам крайних точек, надо из
координат конца вычесть соответствующие
координаты начала:
![]() .
.
Определение
19.
Пусть
![]() - углы между вектором
- углы между вектором![]() и соответственно ортами
и соответственно ортами
![]() ,
,![]() ,
,![]() (рис. 9), тогда направляющие
косинусы
вектора
(рис. 9), тогда направляющие
косинусы
вектора
![]() определяются по правилу:
определяются по правилу:
![]() ,
,
![]() ,
,
![]() ,
,
Следовательно,
сумма квадратов направляющих косинусов
равна
![]() :
:![]() .
.
Пример 1.
Даны точки
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Найти координаты и длину
вектора
![]() .
.
Решение.
Найдем координаты векторов
![]() и
и![]() :
:
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
По правилам действий с векторами, получим:
![]() и
и![]() }.
}.
Теперь находим длину искомого вектора:
![]() =
=![]() =
=![]() .
.
Пример 2.
Даны точки
![]() ,
,
![]() .
.
Найти направляющие косинусы
вектора
![]() .
.
Решение.
Так как
![]() ,
то
,
то![]() и направляющие косинусы находятся
согласно формулам:
и направляющие косинусы находятся
согласно формулам:
![]() ,
,
![]() ,
,![]() .
.
Связь компонент, проекций, направляющих косинусов и коэффициентов в разложении по базису.
Пусть
вектор
![]() в пространстве
в пространстве![]() ;
;
![]() ,
,![]() ,
,![]() - ортонормированный базис в данной
системе координат,
- ортонормированный базис в данной
системе координат,
![]() - углы между вектором
- углы между вектором![]() и соответственно ортами
и соответственно ортами
![]() ,
,![]() ,
,![]() .
Тогда
.
Тогда
![]() ,
,
где
![]() ,
,
![]() ,
,
![]() -составляющие вектора
-составляющие вектора
![]() ,
,![]() - координаты вектора
- координаты вектора![]() в базисе
в базисе
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Деление отрезка в данном отношении.
Пусть
![]() ,
,![]() .
Координаты точки
.
Координаты точки![]() на отрезке
на отрезке![]() ,
которая делит этот отрезок в отношении
,
которая делит этот отрезок в отношении![]() ,
т.е.
,
т.е.![]() ,
определяются по формулам:
,
определяются по формулам:
![]() ,
,
![]() ,
,
![]() .
.
Координаты
середины отрезка
![]() соответствуют значению
соответствуют значению![]() и определяются как полусумма координат
концов отрезка:
и определяются как полусумма координат
концов отрезка:
![]() ,
,
![]() ,
,
![]() .
.
5. Линейные операции над векторами, заданными своими координатами.
Пусть
![]() и
и![]() .
.
При умножении вектора на число каждая координата вектора умножается на это число:
 ,
,
 ,
тогда
,
тогда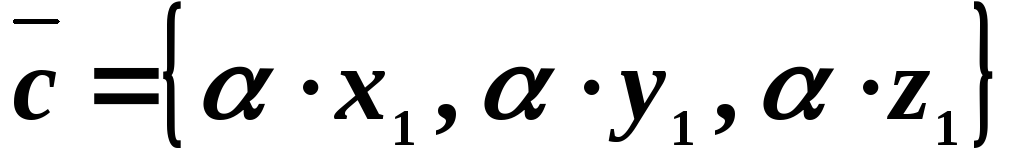 .
.При сложении (вычитании) векторов их одноименные проекции складываются (вычитаются):
 ,
тогда
,
тогда
 .
.
5.А. Скалярное произведение векторов.
Определение 20. Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
Обозначается
скалярное произведение символом
![]() или
или![]() .
.
Скалярное произведение векторов можно выразить формулами:
![]()
Отсюда скалярное произведение двух векторов равно произведению длины одного вектора на проекцию на него другого.
П усть
вектор перемещения
усть
вектор перемещения![]() будет неподвижен, а точка приложения
вектора силы
будет неподвижен, а точка приложения
вектора силы![]() скользит вдоль вектора
скользит вдоль вектора![]() ,
тогда
,
тогда
![]()
есть работа, совершаемая
под действием силы
![]() вдоль вектора
вдоль вектора![]() .
.
П ример
3. Вычислить, какую
работу производит сила
ример
3. Вычислить, какую
работу производит сила
![]() ,
когда точка ее приложения перемещается
из
,
когда точка ее приложения перемещается
из![]() в
в![]() .
.
Решение.
Образуем вектор перемещения
![]() .
.
Тогда работа
![]() .
.
Скалярное произведение векторов, заданных своими координатами.
Пусть
![]() и
и![]() тогда
тогда
![]() .
.
Скалярное произведение векторов, заданных своими координатами, равно сумме произведений одноименных координат.
