
- •19 Vektor
- •2. Линейные операции над векторами.
- •Свойства линейных операций над векторами.
- •3. Понятие линейной зависимости векторов.
- •4. Понятие о проекциях.
- •Декартова система координат.
- •Связь компонент, проекций, направляющих косинусов и коэффициентов в разложении по базису.
- •Деление отрезка в данном отношении.
- •5. Линейные операции над векторами, заданными своими координатами.
- •5.А. Скалярное произведение векторов.
- •Свойства скалярного произведения.
- •5.Б. Векторное произведение.
- •Векторное произведение двух векторов, заданных своими проекциями.
- •Механический смысл векторного произведения.
- •Свойства векторного произведения векторов.
- •5.В. Смешанное произведение трех векторов.
- •Смешанное произведение векторов, заданных своими координатами.
- •Свойства смешанного произведения.
19 Vektor
ВЕКТОРНАЯ АЛГЕБРА
Оглавление.
1. Понятие вектора.
2. Линейные операции над векторами.
3. Понятие линейной зависимости векторов.
4. Понятие о проекциях.
5. Линейные операции над векторами, заданными своими координатами.
5.а. Скалярное произведение векторов.
5.б. Векторное произведение.
5.в. Смешанное произведение трех векторов.
1. Понятие вектора
Все величины бывают скалярные и векторные. Скалярной величиной или скаляром называется величина, которая вполне определяется своим численным значением.
Примеры
физических скалярных величин:
![]() -температура;
-температура;![]() - масса;
- масса;![]() - плотность;
- плотность;![]() - длина;
- длина;![]() - площадь и т.д.
- площадь и т.д.
Вектором или векторной величиной называется величина, которая характеризуется не только своим численным значением, но и определенным направлением в рассматриваемом пространстве.
Векторы - сила, скорость, ускорение, напряженность электрического поля.
Определение 1. Направленный отрезок (или, и что то же, упорядоченная пара точек - начало и конец отрезка) называется вектором.

Геометрическое изображение вектора:
Обозначение
вектора:
![]() ,
либо
,
либо![]() либо жирной строчной буквой
либо жирной строчной буквой![]() .
Направление на отрезке обозначается
стрелкой.
.
Направление на отрезке обозначается
стрелкой.
Численное
значение вектора называется его модулем
или абсолютной величиной и обозначается:
![]() ,
,![]() .
.
Нулевой
вектор – это вектор у которого начало
и конец совпадают. Он обозначается
![]() и его модуль равен нулю, а направление
неопределенно.
и его модуль равен нулю, а направление
неопределенно.
Определение
2.
Векторы называются коллинеарными,
если они расположены на одной прямой
или на параллельных прямых. Обозначают:
![]() .
.
Определение 3. Векторы называются компланарными, если существует плоскость, которой они параллельны.
Определение 4. Два вектора называются равными, если они коллинеарные, одинаково направлены и имеют одинаковую длину.
Из этого определения следует, что мы будем изучать свободные векторы. То есть вектор параллельно самому себе, не изменяя направления, можно переносить в любую точку пространства.
Векторы являются предметом векторного исчисления подобно тому, как числа являются предметом арифметики или алгебры.
2. Линейные операции над векторами.
К линейным операциям над векторами относятся операции умножения вектора на число и сложение векторов.
Определение
5.
Под произведением вектора
![]() на число
на число![]() понимается вектор
понимается вектор
![]() ,
удовлетворяющий следующим условиям:
,
удовлетворяющий следующим условиям:
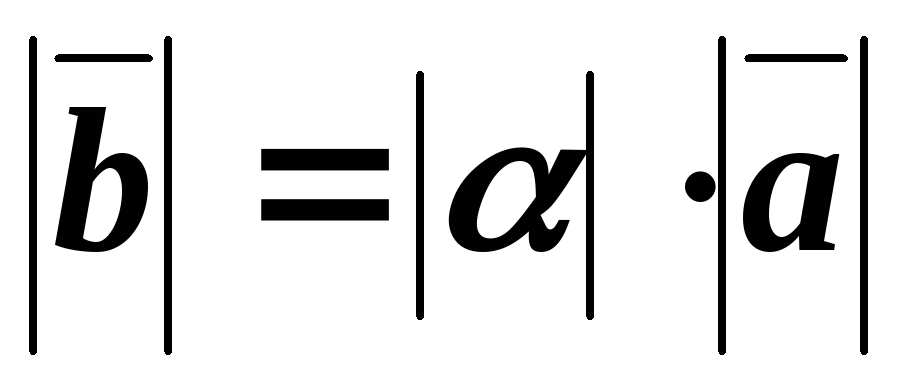 ;
;вектор
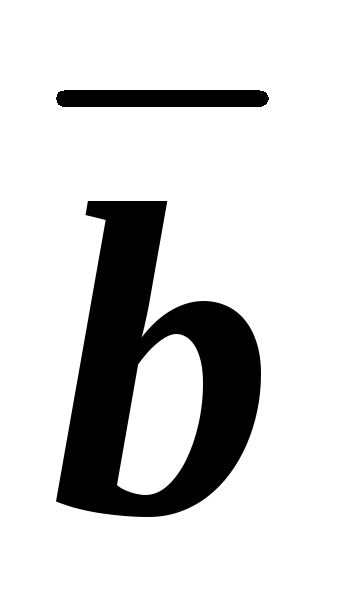 коллинеарен вектору
коллинеарен вектору
 (
( );
);
векторы
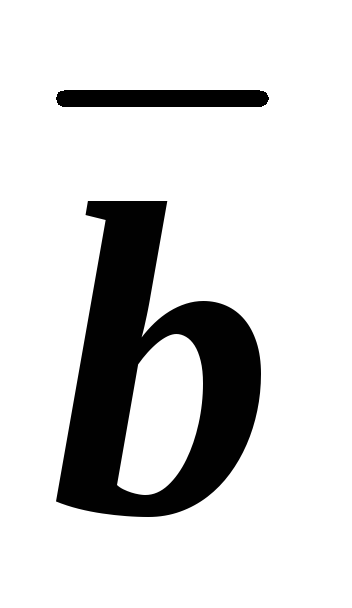 и
и
 направлены одинаково, если
направлены одинаково, если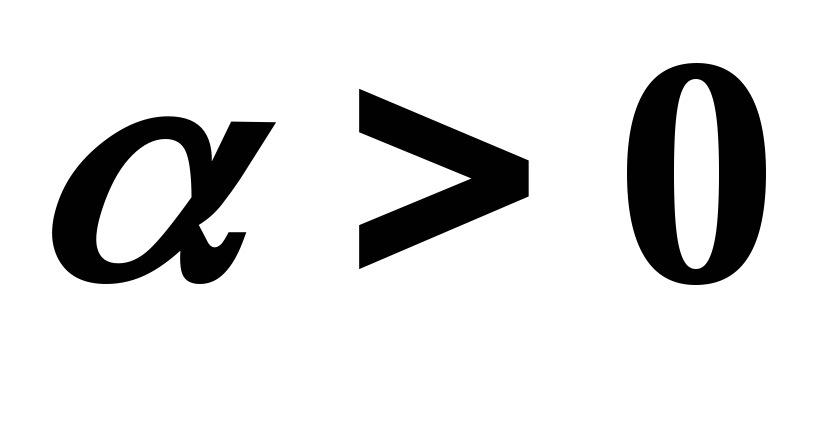 и противоположно, если
и противоположно, если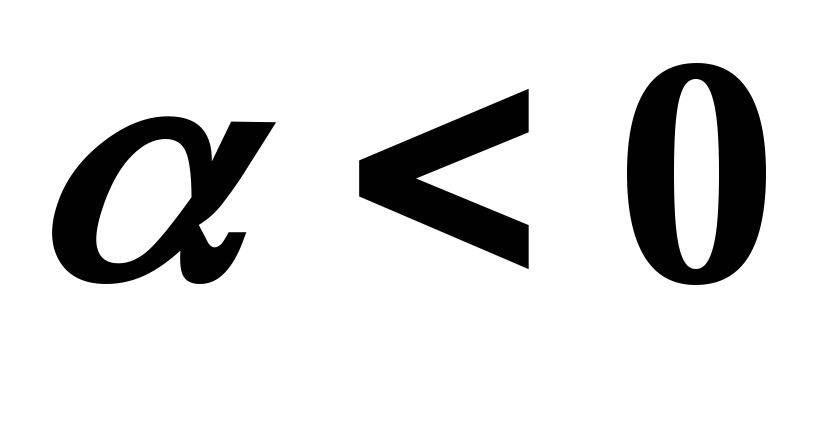 .
.
Произведение
вектора
![]() на число
на число![]() обозначается
обозначается![]() .
.
Замечание
1.
Пусть
![]() ,
рассмотрим вектор
,
рассмотрим вектор![]() ,
тогда
,
тогда![]() .
Векторы
.
Векторы![]() и
и![]() коллинеарные и одинаково направлены,
тогда
коллинеарные и одинаково направлены,
тогда![]() -единичный
вектор,
сонаправленный с
-единичный
вектор,
сонаправленный с
![]() .
Вектор
.
Вектор![]() -орт
вектора
-орт
вектора
![]() , и обозначается
, и обозначается![]() 0,
т.е.
0,
т.е.
![]() и
и![]() или
или![]() .
.
Замечание 2.
Пусть дан вектор
![]() .
Для любого коллинеарного ему вектора
.
Для любого коллинеарного ему вектора
![]() существует и притом одно число
существует и притом одно число
![]() ,
удовлетворяющее равенству
,
удовлетворяющее равенству
![]() .
Тогда
.
Тогда
![]() и
и![]() ,
если
,
если
![]() и
и
![]() одинаково направлены и
одинаково направлены и![]() ,
если они противоположно направлены.
,
если они противоположно направлены.
О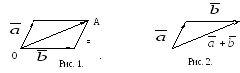 пределение
6.
Суммой
двух векторов
пределение
6.
Суммой
двух векторов
![]() и
и
![]() ,
приведенных к общему началу, является
диагональ параллелограмма (
,
приведенных к общему началу, является
диагональ параллелограмма (![]() см. рис. 1), построенного на этих векторах
как на сторонах (правило
параллелограмма).
Правило
треугольника:
см. рис. 1), построенного на этих векторах
как на сторонах (правило
параллелограмма).
Правило
треугольника:
начало следующего вектора поместить в конец предыдущего и вектор, соединяющий начало первого с концом последнего есть вектор суммы (см. рис. 2).
Ч тобы
сложить несколько векторов, достаточно
начало каждого последующего вектора
совместить с концом предыдущего, тогда
замыкающий вектор, идущий из начала
первого в конец последнего, будет
вектором суммы (правило многоугольника
см. рис. 3).
тобы
сложить несколько векторов, достаточно
начало каждого последующего вектора
совместить с концом предыдущего, тогда
замыкающий вектор, идущий из начала
первого в конец последнего, будет
вектором суммы (правило многоугольника
см. рис. 3).
Если
точка
![]() совпадает с точкой
совпадает с точкой![]() ,
то сумма векторов равна нулю.
,
то сумма векторов равна нулю.
Определение
7.
Вектором,
противоположным
к данному
вектору
![]() ,
называется вектор
,
называется вектор![]() ,
модуль которого равен модулю вектора
,
модуль которого равен модулю вектора![]() ,
а направление противоположно (см. рис.
4).
,
а направление противоположно (см. рис.
4).
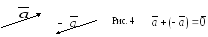
Определение
8.
Под
разностью
двух векторов
![]() и
и
![]() понимается такой третий вектор
понимается такой третий вектор
![]() ,
который при сложении с вычитаемым
вектором
,
который при сложении с вычитаемым
вектором
![]() дает уменьшаемый вектор
дает уменьшаемый вектор
![]() .
.
Правило
построения разности векторов
![]() и
и
![]() :
:
П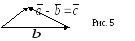 риводим
векторы
риводим
векторы![]() и
и
![]() к общему началу, и соединяем концы
векторов
к общему началу, и соединяем концы
векторов
![]() и
и
![]() .
Вектор разности направлен из конца
вычитаемого вектора (
.
Вектор разности направлен из конца
вычитаемого вектора (![]() )
в конец уменьшаемого вектора (
)
в конец уменьшаемого вектора (![]() см. рис. 5).
см. рис. 5).
