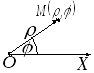- •30 AnGeom
- •2. Прямая линия на плоскости
- •Типы уравнений прямой.
- •3. Угол между двумя прямыми. Условие параллельности и перпендикулярности.
- •Линейные образы в r3
- •4. Понятие алгебраической поверхности.
- •4.А. Плоскость.
- •5. Прямая линия в пространстве.
- •5.А. Канонические уравнения прямой в пространстве.
- •5.Б. Приведение общих уравнений прямой к каноническому виду.
- •6. Угол между двумя прямыми. За угол между двумя прямыми
- •7. Прямая и плоскость.
- •Условие того, что прямая лежит в данной плоскости.
- •Условие того, что две прямые лежат в одной плоскости.
- •8. Кривые второго порядка.
- •8.А Окружность
- •8.Б. Эллипс (в декартовой системе координат)
- •8.В. Гипербола
- •Каноническое уравнение гиперболы
- •8.Г. Парабола
- •Пример 18. Установить, что уравнение
- •Полярная система координат.
- •Связь между прямоугольными и полярными координатами.
Полярная система координат.
При решении многих задач аналитической геометрии оказывается более удобным определять положение точки на плоскости не прямоугольными декартовыми координатами, а так называемыми полярными координатами.
Система
полярных координат задается полюсом -
точкой
![]() и полупрямой, исходящей из полюса («луч»
-
и полупрямой, исходящей из полюса («луч»
-![]() - полярная ось).
- полярная ось).
|
|
|
Чтобы
установить взаимнооднозначное
соответствие между точками плоскости
и координатами этой точки, ограничим
изменение полярного угла
![]() промежутком
промежутком![]() (или иным промежутком длины
(или иным промежутком длины![]() ).
Значения
).
Значения![]() ,
удовлетворяющие этому условию, называют
главными значениями.
Назовем полярные координаты
,
удовлетворяющие этому условию, называют
главными значениями.
Назовем полярные координаты
![]() основными,
если
основными,
если
![]() ,
а
,
а![]() есть главное значение полярного угла,
т.е. если
есть главное значение полярного угла,
т.е. если![]() .
.
Связь между прямоугольными и полярными координатами.
П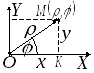 усть
полюс системы координат совпадает с
началом декартовой системы координат,
а полярная ось совпадает с положительной
полуосьюOX.
Тогда из
усть
полюс системы координат совпадает с
началом декартовой системы координат,
а полярная ось совпадает с положительной
полуосьюOX.
Тогда из
![]() :
:
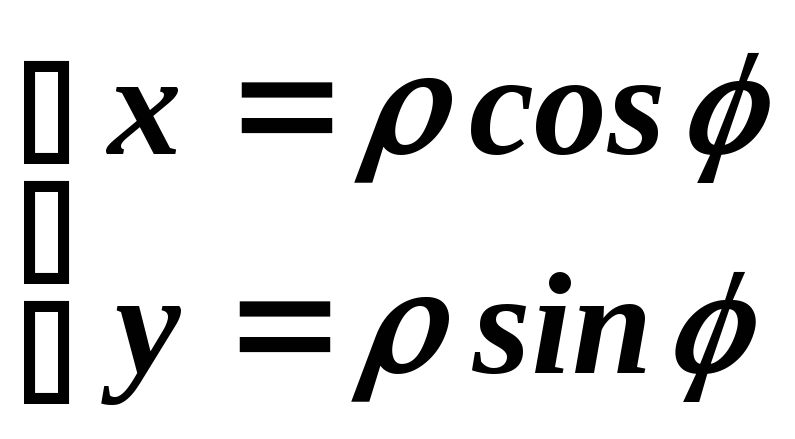
- это формулы перехода к декартовой системе координат.
Выведем формулы обратного перехода от декартовых координат к полярным.
Полярный
радиус – вектор
![]() ,
будучи расстоянием от точки
,
будучи расстоянием от точки![]() до начала координат, будет равен:
до начала координат, будет равен:
![]() ,
а также,
,
а также,
![]() ,
,![]() .
.
Угол
![]() определяется из условия:
определяется из условия:![]() t
и знаков функций
t
и знаков функций
![]() .
.
FVB