Линейные образы в r3

4. Понятие алгебраической поверхности.

Определение. Алгебраической поверхностью называется множество, которое в какой-нибудь декартовой системе координат может быть задано уравнением вида:

где все показатели степени – целые неотрицательные числа. Наибольшая из сумм: называется степенью уравнения, а также периодом алгебраической поверхности. Это определение означает, в частности, что сфера является алгебраической поверхностью второго порядка.

Перейдем к рассмотрению конкретных линейных образов в пространстве R₃.

4.А. Плоскость.

1. У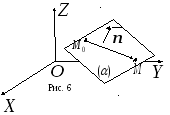равнение плоскости, проходящей через данную точку, перпендикулярно данному вектору (рис. 6).

- текущая точка плоскости . Вектор. Для любой точки плоскости векторыиортогональны, следовательно, их скалярное произведение равно.

.

В уравнении перейдём к координатной форме:

. (12)

Уравнение (12) называется уравнением плоскости, проходящей через данную точку, перпендикулярно данному вектору.

2. Общее уравнение плоскости - это уравнение степени с неизвестными, которое имеет вид:

. (13)

3. Уравнение плоскости, проходящей через три данные точки (рис. 7).

Пусть плоскости принадлежат три точки,,.- текущая точка плоскости, тогда векторы,,компланарны и, следовательно, смешанное произведение этих векторов равно нулю.

, или . (14)

4. Уравнение плоскости «в отрезках»:

(15)

где а,b,с – величины отрезков, отсекаемых плоскостью от начала координат на осях координат (рис. 8).

5. Расстояние точки от плоскости.

Дана плоскость -и точкавне плоскости, тогда расстояниеточки от плоскости имеет вид:

(16)

6. Угол между двумя плоскостями. Условие параллельности и перпендикулярности двух плоскостей (рис. 9).

Даны две плоскости:

и

и ; - нормальные векторы к соответствующим данным плоскостям.

За угол между двумя плоскостями принимается угол между их нормальными векторами:

(17)

Если плоскости параллельны, то векторы иколлинеарны, и, следовательно,

(18)

условие параллельности двух плоскостей.

Если плоскости перпендикулярны, то

(19)

условие перпендикулярности двух плоскостей.

5. Прямая линия в пространстве.

Прямую линию в пространстве можно представить как пересечение двух плоскостей, то есть совокупность двух уравнений плоскостей. Систему двух непараллельных уравнений (плоскостей) называют общими уравнениями прямой:

.

5.А. Канонические уравнения прямой в пространстве.

Каждый не равный нулю вектор, лежащий на данной прямой или параллельный ей, называется направляющим вектором данной прямой и обозначается: .

Если известна точка , прямой и направляющий вектор, то прямая может быть определена (двумя) уравнениями вида:

, (20)

которые называются каноническими уравнениями прямой.

Канонические уравнения прямой, проходящей через две данные точки иимеют вид:

. (21)

Обозначив буквой каждое из равных отношений в канонических уравнениях, мы получим: . Отсюда

. (22)

Уравнения (22) есть параметрические уравнения прямой, проходящей через точку , параллельно вектору. В уравнениях (22)рассматривается как произвольно изменяющийся параметр;- как функции от. При изменениивеличиныменяются так, что точкадвижется по данной прямой.