Лабораторная работа № 23.

RC- цепи.

Цель: Изучение RC- цепей.

Оборудование: Система моделирования Multisim.

ВВЕДЕНИЕ

Напряжение (условное обозначение U, иногда Е). Напряжение между двумя точками – это энергия (или работа), которая затрачивается на перемещение единичного положительного заряда из точки с низким потенциалом в точку с высоким потенциалом (т.е. первая точка имеет более отрицательный потенциал по сравнению со второй). Напряжение называют также разностью потенциалов или электродвижущей силой (э.д.с.). Единицей измерения напряжения служит вольт. Обычно напряжение измеряют в вольтах (В),киловольтах (1 кВ = 10³ В), милливольтах (1 мВ = 10^-3 В) или микровольтах (1 мкВ = 10^-6 В).

Ток (условное обозначение I). Ток – это скорость перемещения электрического заряда. Единицей измерения тока служит ампер. Обычно ток измеряют в амперах (А), миллиамперах (1 мА = 10^-3 А), микроамперах (1 мкА = 10^-6 А), наноамперах (1 нА=10^-9 А). Ток величиной 1А создается перемещением заряда в 1 кулон за время, равное 1 сек. Условились считать, что ток в цепи протекает от точки с более положительным потенциалом к точке с более отрицательным потенциалом, хотя электрон перемещается в противоположном направлении.

Напряжение всегда измеряется между двумя точками схемы, ток всегда протекает через точку в схеме или через какой-нибудь элемент схемы.

Законы Кирхгофа.

1. Сумма токов, втекающих в точку, равна сумме токов вытекающих из нее (сохранение заряда). В электронике эту точку схемы называют узлом. Из этого закона вытекает следствие: в последовательной цепи ток во всех точках одинаков.

2. При параллельном соединении элементов (рис.1) напряжение на каждом из элементов одинаково. Иначе говоря, сумма падений напряжения между точками А и В, измеренная по любой ветви схемы, соединяющей эти точки, одинакова и равна напряжению между точками А и В.

Рис.1

Иногда это правило формулируется так: сумма падений напряжения в любом замкнутом контуре схемы равна нулю.

Пассивные элементы электроники – это элементы способные только ослабить сигнал (резистор, конденсатор, индуктивность).

Резистор. Падение напряжения на участке цепи прямо пропорционально току, протекающему через цепь и обратно пропорционально силе тока: (закон Ома). Объекты, для которых выполняется закон Ома, называют резисторами. Однако, закон Ома выполняется не для всех элементов. Например, ток, протекающий через неоновую лампу, представляет собой нелинейную функцию от приложенного напряжения (он сохраняет нулевое значение до критического значения напряжения, а в критической тоске резко возрастает). То же самое можно сказать и о целой группе других элементов – диодах, транзисторах, лампах.

Резисторы изготавливают из проводящего материала (графита, тонкой металлической или графитовой пленки или провода, обладающего невысокой проводимостью). Сопротивление R измеряется в Омах, если напряжение U выражено в вольтах, а ток I в амперах.

Параметры резисторов:

1. номинальная величина сопротивления R (Ом, кОм, МОм, мОм);

2. допуск + R (в %): для обычных резисторов - + 5%, +10%, для прецинзионных - + 1%, + 0,01%;

3. номинальная мощность – это та мощность, которую резистор способен длительное время рассеивать в пространство без изменения своих свойств (типовые мощности: 0,0625Вт, 0,125Вт).

Последовательное и параллельное соединение резисторов. Из определения сопротивления следуют следующие выводы:

1. сопротивление двух последовательно соединенных резисторов (рис.2 а) равно: R =R₁ +R₂. При последовательном соединении резисторов всегда получаем большее сопротивление, чем сопротивление отдельного резистора.

2. сопротивление двух параллельно соединенных резисторов (рис.2 б) равно . При параллельном соединении резисторов всегда получаем меньшее сопротивление, чем соединение отдельных резисторов.

а) б)

Рис.2. Соединения резисторов.

Маркировка резисторов. Отечественная промышленность для маркировки резисторов использует надписи: Е – Ом, К- КОм, М – МОм. Например, надпись на резисторе 1К8 означает 1,8КОМ, К47 – 0,47КОм, 5М6 – 5,6МОм, 4Е7 – 4,7Ом.

Зарубежная промышленность пользуется цветной маркировкой. На резистор как правило наносится 5 цветных колец. В таблице № 1 представлена цветовая маркировка резисторов.

Табл.№1. Цветовая маркировка резисторов.

цвет	Сопротивление				Допуск (5-я полоса)
	1-я цифра (1-я полоса)	2-я цифра (2-я полоса)	3-я цифра (3-я полоса)	Множитель (4-я полоса)
серебристый				10-2	+10%
золотистый				10-1	+5%
черный		0		1
коричневый	1	1	1	10	+1%
красный	2	2	2	102	+2%
оранжевый	3	3	3	103
желтый	4	4	4	104
зеленый	5	5	5	105	+0,5%
голубой	6	6	6	106	+0,25%
фиолетовый	7	7	7	107	+0,1%
серый	8	8	8	108	+0,05%
белый	9	9	9	109

Номинальное сопротивление резистора выбирается не произвольно, а из стандартного ряда (таблица 2).

Таблица №2.

Обозначение рядов			Обозначение рядов
Е24 (допуск + 5%)	Е12 (допуск + 10%)	Е6 (допуск + 20%)	Е24 (допуск + 5%)	Е12 (допуск + 10%)	Е6 (допуск + 20%)
1,0	1,0	1,0	3,3	3,3	3,3
1,1			3,6
1,2	1,2		3,9	3,9
1,3			4,3
1,5	1,5	1,5	4,7	4,7	4,7
1,6			5,1
1,8	1,8		5,6	5,6
20,			6,8	6,8	6,8
2,2	2,2	2,2	7,5
2,4			8,2	8,2
2,7	2,7		9,1
3,0

Конденсатор – это устройство, имеющее два вывода и обладающее свойством, согласно которому заряд накопленный этим устройством прямо- пропорционален напряжению между выводами, а коэффициент пропорциональности называют емкостью конденсатора (Q= CU).

Конденсатор, имеющий емкость С фарад, к которому приложено напряжение U вольт, накапливает заряд Q кулон на одной пластине и –Q – на другой.

Продифференцировав выражение для Q, получим . Из этого выражения следует вывод, что конденсатор – это более сложный элемент, чем резистор; ток пропорционален не просто напряжению: а скорости изменения напряжения. Если напряжение на конденсаторе, имеющем емкость 1Ф, изменится на 1В за 1сек, то получим ток 1А. И наоборот, протекание тока 1А через конденсатор емкостью 1Ф вызывает изменение напряжения на 1В за 1сек. Емкость, равная 1Ф, очень велика, и поэтому чаще имеют дело с микрофарадами (мкФ) или пикофарадами (пФ).

Основные параметры конденсатора:

1. номинальная емкость;

2. максимальное напряжение – это напряжение, которое длительное время может быть приложено к конденсатору и не вызывать каких-либо изменений его свойств.

3. отклонения конденсатора +С (допуск)

Последовательное и параллельное соединение конденсаторов. Емкость несколько параллельно соединенных конденсаторов равна сумме его емкостей. Нетрудно в этом убедиться: приложим напряжение к параллельному соединению, тогда

CU = Q =Q1 +Q2 +Q3+ … = C1U + C2U +C3U +… = (C1 +C2 +C3 + …)U или С = С1 +С2 +С3 +… .

Для последовательного соединения конденсаторов имеем такое же выражение, как для параллельного соединения резисторов: .

В частном случае для двух конденсаторов: .

Номинальное значение, так же как и резистора выбирается из стандартного ряда (таблица 3). Стандартная величина емкости определяется по формуле С = a * 10ⁿ, n =0,1,2,3,… Значения коэффициентов a приведены в таблице 3.

Таблица №3.

Обозначение рядов			Обозначение рядов
Е24 (допуск + 5%)	Е12 (допуск + 10%)	Е6 (допуск + 20%)	Е24 (допуск + 5%)	Е12 (допуск + 10%)	Е6 (допуск + 20%)
1,0	1,0	1,0	3,3	3,3	3,3
1,1			3,6
1,2	1,2		3,9	3,9
1,3			4,3
1,5	1,5	1,5	4,7	4,7	4,7
1,6			5,1
1,8	1,8		5,6	5,6
20,			6,8	6,8	6,8
2,2	2,2	2,2	7,5
2,4			8,2	8,2
2,7	2,7		9,1
3,0

RC- цепи: изменения во времени напряжения и тока. Для анализа цепей переменного тока (или в общем случае схем, работающих с изменяющимися напряжениями и токами) можно использовать характеристики двух типов. Во-первых, можно рассматривать изменения напряжения U и тока I во времени, а во-вторых, - изменение амплитуды при изменении частоты сигнала. И те, и другие характеристики имеют свои преимущества, и в каждом практическом случае приходится выбирать наиболее подходящие.

Чтобы ответить на вопрос, какими свойствами обладают схемы, в состав которых входят конденсаторы, рассмотрим простейшую RC- цепь (рис.3).

Рис.3. RC- цепь. Рис.4. Сигнал разряда RC- цепи.

Воспользуемся полученным ранее выражением для емкости: . Это выражение представляет собой дифференциальное уравнение, решение которого имеет вид e^-t/RC . отсюда следует, что если заряженный конденсатор подключить к резистору, то он будет разряжаться так, как показано на рис.4.

Постоянная времени. Произведение RC называют постоянной времени цепи. Если R измерять в омах, C – в фарадах, то произведение RC будет измеряться в секундах. Для конденсатора емкость 1мкФ, подключенного к резистору сопротивлением 1кОм, постоянная времени составляет 1мс. Если конденсатор был предварительно заряжен и напряжение на нем составляет 1В, то при подключении резистора в цепи появится ток, равный 1мА.

Рис.5. RC- цепь. Рис.6.

На рис.5 показана несколько иная схема. В момент времени t =0 схема подключается к батарее. Уравнение, описывающее работу такой схемы, выглядит следующим образом: I =C(dU/dt) =(Uвх - Uвых)/R и имеет решение Uвых = Uвх + Ae^-t/RC. Постоянная величина А определяется из начальных условий (рис.6): U =0 при t =0, откуда A = -Uвх и Uвых =Uвх (1 – e^-t/RC).

Установление равновесия. При условии t >> RC напряжение достигает значения Uвх (правило пяти: за время равное пяти постоянным времени, конденсатор разряжается или заряжается на 99%). Если затем изменить входное напряжение Uвх (сделать его, например, равным нулю), то напряжение на конденсаторе U будет убывать, стремясь к новому значению по экспоненциальному закону e^-t/RC. Например, если на вход подать прямоугольный сигнал Uвх, то сигнал на выходе Uвых будет иметь форму, показанную на рис.7.

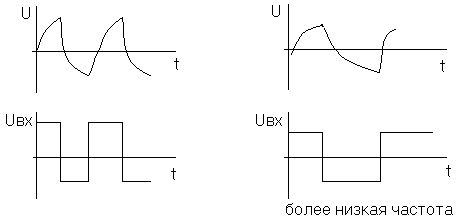
Рис.7. Напряжение, снимаемое с конденсатора

(верхние сигналы), при условии, что на него через

резистор подается прямоугольный импульс.

Здесь возникает вопрос: каков закон изменения для произвольного Uвх(t)? Для того чтобы ответить на него, нужно решить неоднородное дифференциальное уравнение. В результате получим:

Uвх e ^{- (t- ) / RC}dt.

Согласно полученному выражению, RC- цепь усредняет входное напряжение с коэффициентом пропорциональности e^{- t / RC}, где t =  -t.

Дифференцирующие цепи. Рассмотрим схему, изображенную на рис.8. Напряжение на конденсаторе С равно Uвх –Uвых, поэтому I = Cd(Uвх -Uвых)/dt = Uвых/R.

Рис.8. Дифференцирующая RC- цепь.

Если резистор и конденсатор выбрать так, чтобы сопротивление R и емкость C были достаточно малыми и выполнялось условие dUвых/dt << dUвх/dt, то

C(dUвх/dt) = Uвых/R или Uвых(t) = RC [dUвх(t)/dt].

Таким образом, мы получили, что выходное напряжение пропорционально скорости изменения входного сигнала.

Для того, чтобы выполнялось условие dUвых/dt << dUвх/dt, произведение RC должно быть небольшим, но при этом сопротивление R не должно быть слишком малым, чтобы не «нагружать» выход (при скачке напряжения на входе изменение напряжения на конденсаторе равно нулю и R представляет собой нагрузку со стороны выхода схемы). Если на вход схемы подать прямоугольный сигнал, то сигнал на выходе будет иметь вид, представленный на рис.9.

Рис.9. Входной и выходной сигналы

дифференцирующей RC- цепи.

Дифференцирующие цепи удобно использовать для выделения переднего и заднего фронтов импульсных сигналов. В цифровых схемах можно иногда встретить цепи, подобные той, которая показана на рис.10.

Рис.10. Выделение переднего фронта импульса.

Дифференцирующая RC- цепь генерирует импульсы в виде коротких пиков в моменты переключения входного сигнала, а выходной буферный усилитель преобразует эти импульсы в короткие прямоугольные импульсы. В реальных схемах отрицательный пик бывает небольшим благодаря встроенному в буфер диоду.

Интегрирующие цепи. Рассмотрим схему, изображенную на рис.11. Напряжение на резисторе R равно Uвх –Uвых, следовательно I = C(dU/dt) =(Uвх - Uвых)/R. Если обеспечить выполнение условия Uвых << Uвх за счет большего значения произведения RC, то получим С(dUвых/dt)Uвх/R или Uвых(t) = Uвх(t)dt + const.

Рис.11. Интегрирующая RC- цепь.

Мы получили, что схема интегрирует входной сигнал во времени. На рис.12 показано, как с помощью RC- цепи можно получить задержанный импульс. В виде треугольников изображены КМОП – буферные усилители. Они дают более высокий уровень на выходе (более половины величины напряжения питания постоянного тока) и наоборот. Первый буферный усилитель воспроизводит входной сигнал и обеспечивает небольшое выходное сопротивление, предотвращая тем самым воздействие на источник сигнала RC- цепи. Согласно характеристике RC- цепи, выходной сигнал для нее задерживается относительно входного, поэтому выходной буферный усилитель переключается на 10 мкс позже скачка напряжения на входе (напряжение на выходе RC- цепи достигает 50% своего максимального значения через 0,7RC). Подобную схему используют для того, чтобы задержать импульс на время, в течении которого может произойти какое-либо событие.

Рис.12. Использование RC- цепи для формирования

задержанного цифрового сигнала.

Отметим, что условие Uвых <<Uвх равносильно тому, что ток пропорционален напряжению Uвх. Если бы в качестве входного сигнала выступал бы ток I(t), а не напряжение, то мы получили бы идеальный интегратор. Источником тока может служить резистор с большим сопротивлением и с большим падением напряжения на нем, и на практике часто пользуются этим приближением.

Интегрирующие цепи находят широкое применение в аналоговой технике. Их используют в управляющих системах, схемах с обратной связью, при аналогово-цифровом преобразовании и генерации колебаний.