Задание 40
1.
Производная функции f(x,y)
по направлению вектора s
=
![]() определяется формулой
определяется формулой![]() … .
… .
2. Градиентом функции z = f(x,y) называется вектор grad(z) = {…;…}.
3.
В данной точке для всех векторов s
![]() = … .
= … .
4.
В данной точке для всех векторов s
![]() = … .
= … .
5.
В данной точке
![]() = 0, если направление вектораs
… .
= 0, если направление вектораs
… .
6.
В данной точке
![]() максимальна, если направление вектораs
… .
максимальна, если направление вектораs
… .
7.
В данной точке
![]() минимальна, если направление вектораs
… .
минимальна, если направление вектораs
… .
8.
Если направление вектора s
совпадает с направлением оси Ох,
то производная функции f(x,y)
по направлению
![]() … .
… .
9.
Если направление вектора s
противоположно направлению оси Ох,
то производная функции f(x,y)
по направлению
![]() … .
… .
10.
Если направление вектора s
совпадает с направлением оси Оу,
то производная функции f(x,y)
по направлению
![]() … .
… .
Задание 41
Функция полных
издержек двухпродуктовой фирмы задана
уравнением:
![]() ,
где
,
где
![]() и
и
![]()
объемы выпуска товаров первого и второго
видов соответственно. Построить на
плоскости
объемы выпуска товаров первого и второго
видов соответственно. Построить на
плоскости
![]() линию
постоянных издержек (изокосту)
линию
постоянных издержек (изокосту)
![]() и множество производственных возможностей,
ограниченное издержками производства
в объеме
и множество производственных возможностей,
ограниченное издержками производства
в объеме![]() (задачи
6-10).
(задачи
6-10).
1)
![]() ,
,![]() ;
;
2)
![]() ,
,![]() ;
;
3)
![]() ,
, ![]() ;
;
4)
![]() ,
, ![]() ;
;
5)
![]() ,
,![]() ;
;
6)
![]() ,
,![]() ;
;
7)
![]() ,
,![]() ;
;
8)
![]() ,
, ![]() ;
;
9)
![]() ,
, ![]() ;
;
10)
![]() ,
,![]() .
.
Задание 42
Фирма производит
товар двух видов в количествах x
и y.
Функция полных издержек определена
соотношением
![]() .
Цены этих товаров на рынке равны
.
Цены этих товаров на рынке равны
![]() и
и
![]() соответственно.
Определите, при каких объемах выпуска
достигается максимальная прибыль и
чему она равна, если полные издержки не
превосходят
соответственно.
Определите, при каких объемах выпуска
достигается максимальная прибыль и
чему она равна, если полные издержки не
превосходят
![]() .
.
1)
![]() ;
; ![]() ;
;![]() ;
; ![]() ;
;
2)
![]() ;
; ![]() ;
;![]() ;
; ![]() ;
;
3)
![]() ;
; ![]() ;
;![]() ;
; ![]() ;
;
4)
![]() ;
; ![]() ;
;![]() ;
; ![]() ;
;
5)
![]() ;
; ![]() ;
;![]() ;
; ![]() ;
;
6)
![]() ;
; ![]() ;
;![]() ;
; ![]() ;
;
7)
![]() ;
; ![]() ;
;![]() ;
;![]() ;
;
8)
![]() ;
; ![]() ;
;![]() ;
;![]() ;
;
9)
![]() ;
; ![]() ;
;![]() ;
;![]() ;
;
10)
![]() ;
; ![]() ;
;![]() ;
;![]() .
.
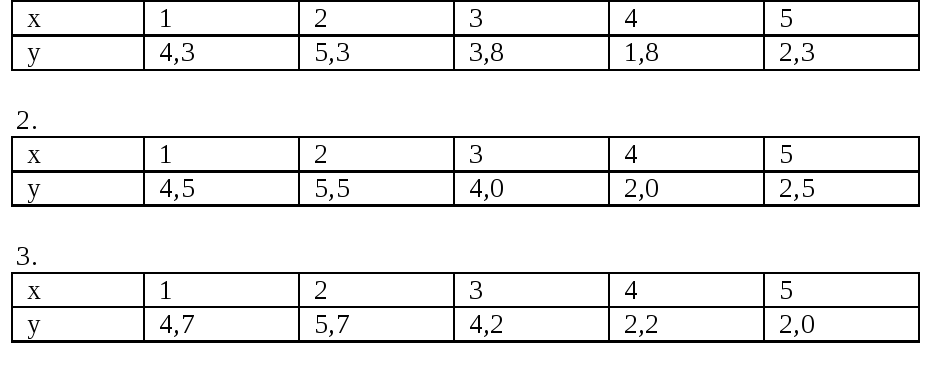
Задание 43
Экспериментально
получены пять значений искомой функции
![]() при пяти значениях аргумента, которые
записаны в таблице. Методом наименьших
квадратов найти функцию
при пяти значениях аргумента, которые
записаны в таблице. Методом наименьших
квадратов найти функцию![]() в виде
в виде![]() .
.
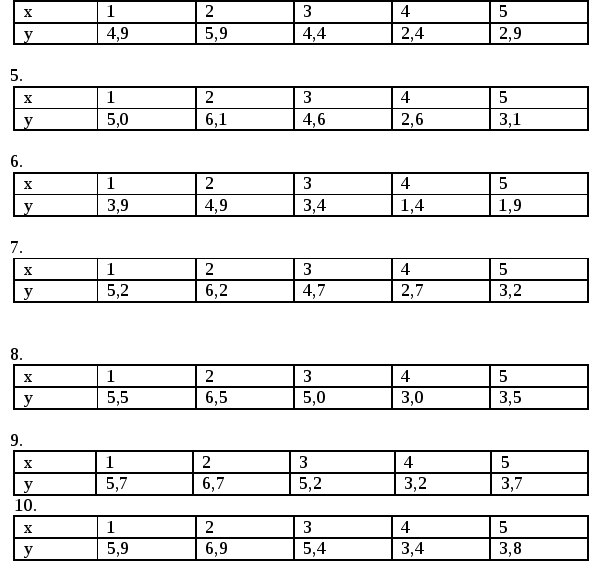
1.
4.