
- •1. Развитие математической модели нечеткой случайной величины для решения задач портфельного анализа.
- •1.1. Определение нечеткой случайной величины.
- •1.2. Определение числовых характеристик нечеткой случайной величины.
- •1.3. Расчет числовых характеристик нечетких случайных величин в классах параметризованных распределений.
- •1.4. Взвешенная сумма нечетких случайных величин.
- •1.5. Выводы по первой главе диссертации.
- •2. Постановки задач портфельного анализа в условиях нечетких случайных данных и методы их решения.
- •2.1. Доходность портфеля в условиях нечетких случайных данных.
- •2.2. Модели портфельного анализа в условиях нечетких случайных данных.
- •2.2.2. Модель максимизации возможности (необходимости) достижения нечеткого уровня ожидаемой доходности при фиксированном уровне риска.
- •2.2.3. Модель максимизации с заданной возможностью (необходимостью) ожидаемого дохода при фиксированном уровне возможного риска.
- •Теорема доказана.
- •2.2.4. Модель минимизации возможного риска при заданном уровне возможного дохода.
- •2.3. Обобщение двумерного портфеля на случай нечетких случайных данных.
- •2.3. Выводы по второй главе диссертации.
2.2. Модели портфельного анализа в условиях нечетких случайных данных.
Перейдем к построению моделей портфельного анализа, позволяющих учитывать один из критериев принятия решений – ожидаемую доходность портфеля как нечеткую величину. Для этого нам необходимо привлечь соответствующие принципы принятия решения в условиях нечетких данных [94] и сформировать модели принятия решений.
2.2.1. Модель максимизации ожидаемого дохода при заданном уровне риска.
В соответствии с классическим подходом модель должна быть записана в следующей форме:
![]() (2.1.1)
(2.1.1)
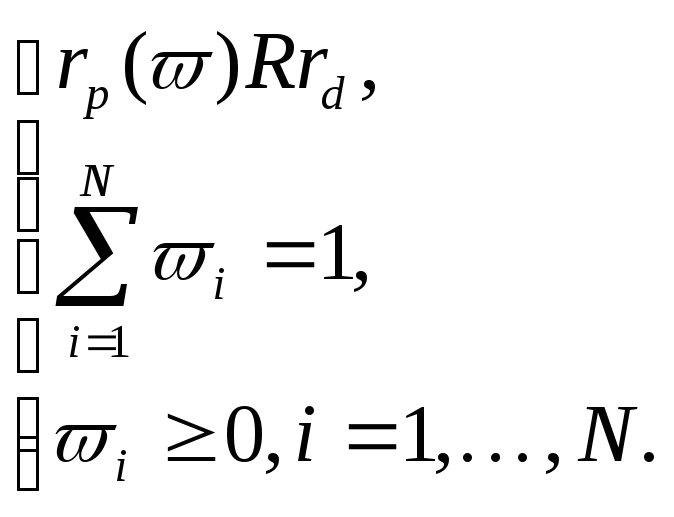 (2.1.2)
(2.1.2)
В данной модели
![]() есть четкое бинарное отношение:
есть четкое бинарное отношение:![]() ,
,![]() есть
приемлемый уровень риска, на который
готов пойти инвестор.
есть
приемлемый уровень риска, на который
готов пойти инвестор.
Однако представленная модель является недостаточно корректной, так как ожидаемая доходность портфеля есть нечеткая величина (2.1).
В связи с этим требуется введение дополнительного принципа принятия решений, уже в условиях нечетких данных [94].
Одним из них является переход к модальным значениям соответствующих нечетких величин. Его применение приводит к следующей модели:
![]() , (2.1.3)
, (2.1.3)
 (2.1.4)
(2.1.4)
где
![]() обозначает переход к модальным значениям
нечетких величин.
обозначает переход к модальным значениям
нечетких величин.
Согласно результатам, представленными в первой главе диссертации,
![]() .
.
Если нечеткие
случайные величины
![]() при фиксированном
при фиксированном![]() принадлежат классу
принадлежат классу
![]() ,
то
,
то
![]() .
Пусть
.
Пусть
![]() ,
т.е.
,
т.е.![]() .
Тогда, принимая во внимание доказанную
в первой главе лемму 1.4.2, мы получаем
при
.
Тогда, принимая во внимание доказанную
в первой главе лемму 1.4.2, мы получаем
при![]() следующую модель, эквивалентную (2.1.1),
(2.1.2),
следующую модель, эквивалентную (2.1.1),
(2.1.2),
![]() , (2.1.5)
, (2.1.5)
 (2.1.6)
(2.1.6)
Полученная задача (2.1.5)-(2.1.6) есть задача квадратичного программирования. Она может быть решена стандартными методами [8].
2.2.2. Модель максимизации возможности (необходимости) достижения нечеткого уровня ожидаемой доходности при фиксированном уровне риска.
Следующий подход к решению задачи связан с ее рассмотрением в рамках модели нечеткого целевого программирования [59]. Его применение приводит к следующей модели:
![]() (2.2.1)
(2.2.1)
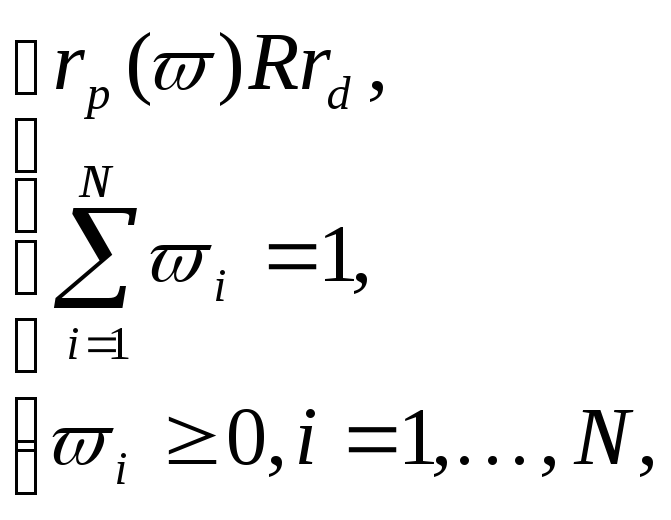 (2.2.2)
(2.2.2)
где
![]() ,
,![]() есть четкое бинарное отношение:
есть четкое бинарное отношение:![]() ,
,![]() есть нечеткий уровень притязаний
критерия, приемлемый для инвестора.
есть нечеткий уровень притязаний
критерия, приемлемый для инвестора.
Рассмотрим сначала
случай
![]() ,
,![]() в модели критерия задачи. Тогда модель
(2.2.1)-(2.2.2) имеет эквивалентную, которая
может быть записана в форме
в модели критерия задачи. Тогда модель
(2.2.1)-(2.2.2) имеет эквивалентную, которая
может быть записана в форме
![]() (2.2.3)
(2.2.3)
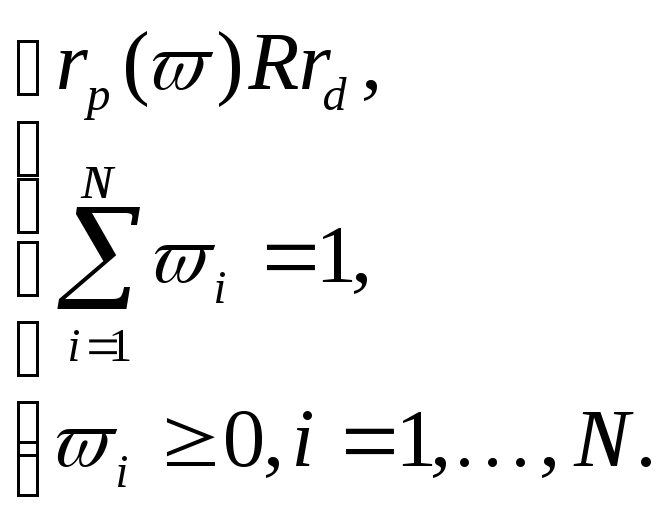 (2.2.4)
(2.2.4)
Прежде чем доказать теорему, позволяющую построить детерминированный эквивалент модели (2.2.3)-(2.2.4), приведем необходимую для ее доказательства лемму [59].
Лемма 2.2.1.
Пусть
![]() где
где![]() -минисвязные
нечеткие величины, определенные на
возможностном пространстве
-минисвязные
нечеткие величины, определенные на
возможностном пространстве![]() ,
,![]() .
Тогда:
.
Тогда: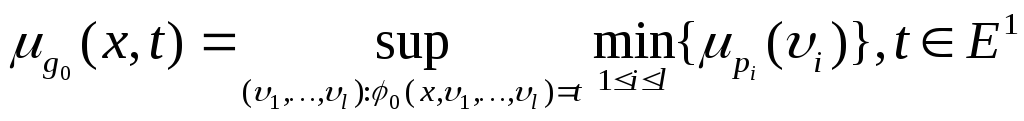 .
.
Теперь мы готовы сформулировать и доказать следующую теорему.
Теорема 2.2.1.
Пусть в задаче (2.2.3)-(2.2.4) возможностные
параметры
![]() ,
,![]() являются минисвязанными, тогда задача
(2.2.3)-(2.2.4) имеет эквивалентный
детерминированный аналог следующего
вида:
являются минисвязанными, тогда задача
(2.2.3)-(2.2.4) имеет эквивалентный
детерминированный аналог следующего
вида:
![]() , (2.2.5)
, (2.2.5)
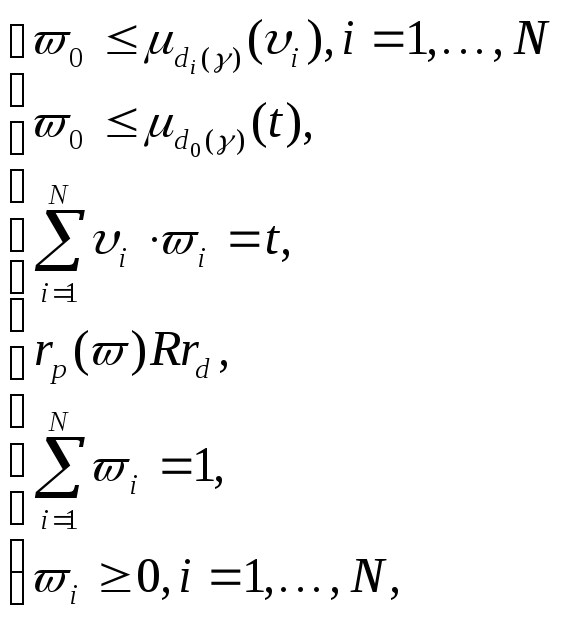 (2.2.6)
(2.2.6)
где
![]() -дополнительная
переменная.
-дополнительная
переменная.
Доказательство.
На основании определения меры возможности преобразуем целевую функцию следующим образом:
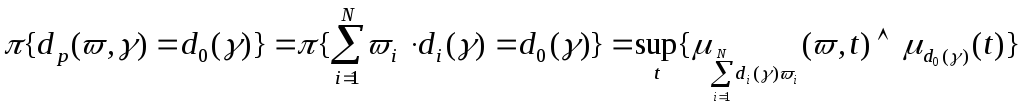 .
.
С учетом полученной формулы и леммы 2.2.1 исходная задача эквивалентна следующей задаче математического программирования.
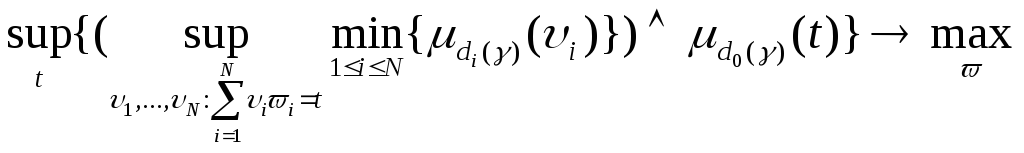 .
.
Путем введения
дополнительной переменной
![]() [59] модель критерия сводится к эквивалентной
модели - задаче математического
программирования.
[59] модель критерия сводится к эквивалентной
модели - задаче математического
программирования.
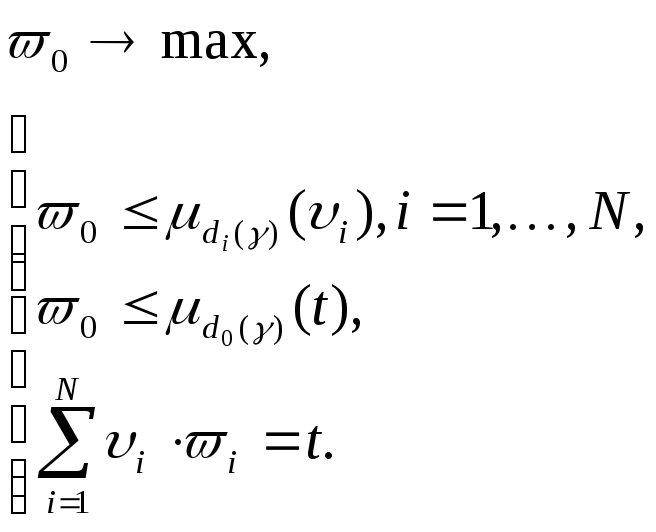
С учетом модели ограничений (2.2.4) мы получаем утверждение теоремы.
Теорема доказана.
Полученная модель допускает сведение к сепарабельной задаче при некоторых дополнительных условиях.
Действительно.
Преобразуем ограничение
![]() .
.
Для этого воспользуемся следующим равенством:
![]() .
.
Введем дополнительные
переменные:![]() .
.
Тогда наше
ограничение примет следующий вид:
![]() .
.
Это есть сепарабельное ограничение.
В результате наша задача (2.2.5)-(2.2.6) сводится к задаче математического программирования следующего вида.
![]() , (2.2.7)
, (2.2.7)
 (2.2.8)
(2.2.8)
Таким образом, мы получили детерминированный аналог для задачи максимизации возможности достижения нечеткого уровня ожидаемой доходности при фиксированном уровне риска.
Далее, преобразуя
выражение для дисперсии по уже известной
формуле (теорема 1.4.1), а также принимая
![]() ,
получаем:
,
получаем:
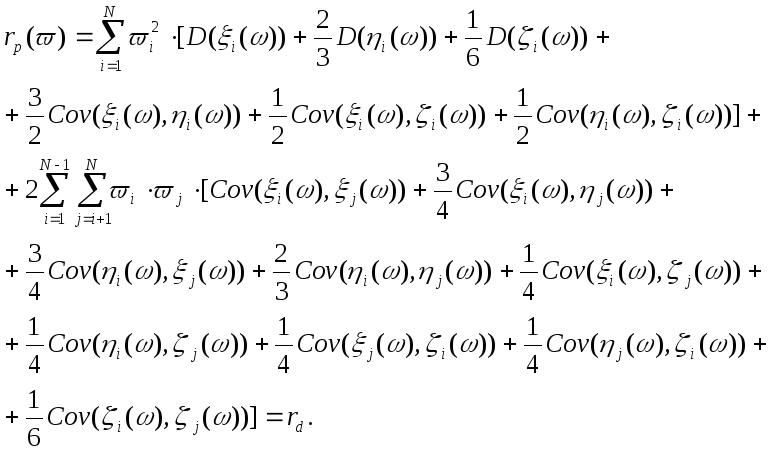
Если предположить, что параметры возможностного распределения являются независимыми случайными величинами, то
![]() .
.
В результате наша задача (2.2.7)-(2.2.8) сводится к следующей сепарабельной задаче.
![]() , (2.2.9)
, (2.2.9)
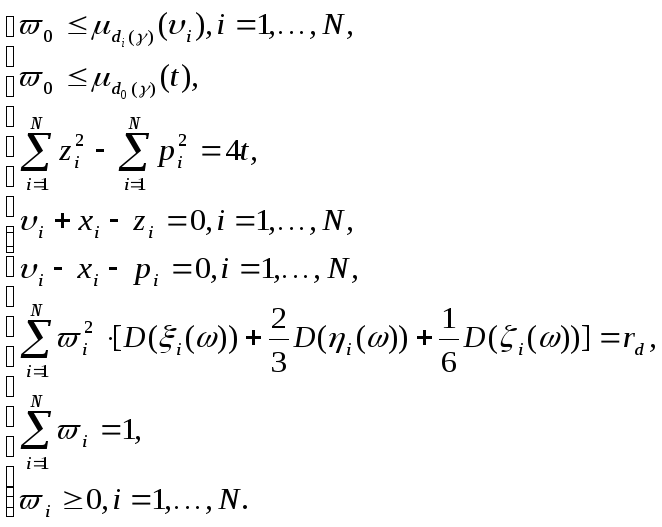 (2.2.10)
(2.2.10)
Уточним полученную модель (2.2.9)-(2.2.10) для некоторых классов распределений.
Пусть
![]() ,
,
![]() .
Тогда модель (2.2.9)-(2.2.10) может быть
преобразована к следующей эквивалентной
модели:
.
Тогда модель (2.2.9)-(2.2.10) может быть
преобразована к следующей эквивалентной
модели:
![]() , (2.2.11)
, (2.2.11)
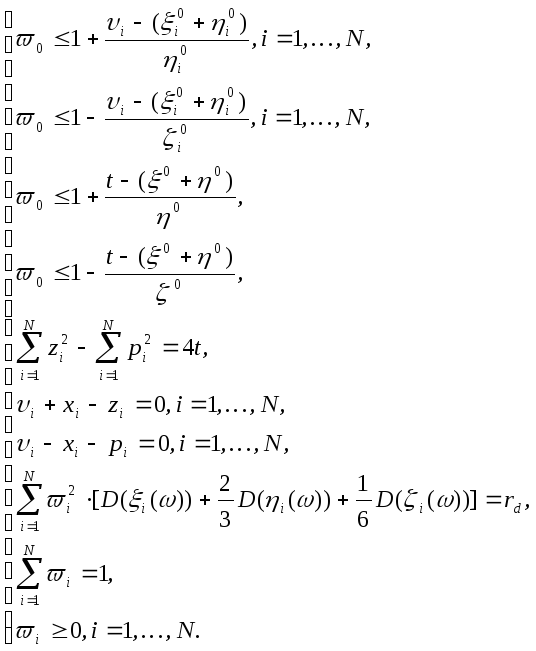 (2.2.12)
(2.2.12)
При ее построении мы учитываем вид распределений и то, что получающееся при этом неравенство
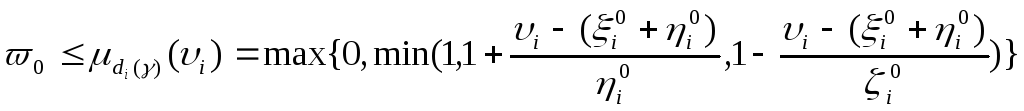
эквивалентно двум неравенствам
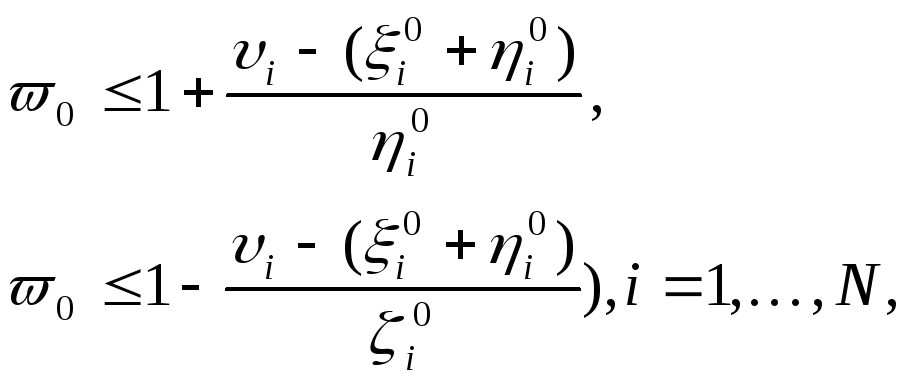
а неравенство
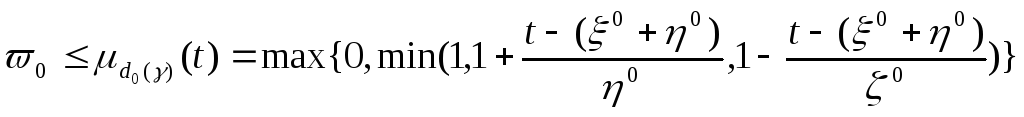
эквивалентно следующим неравенствам
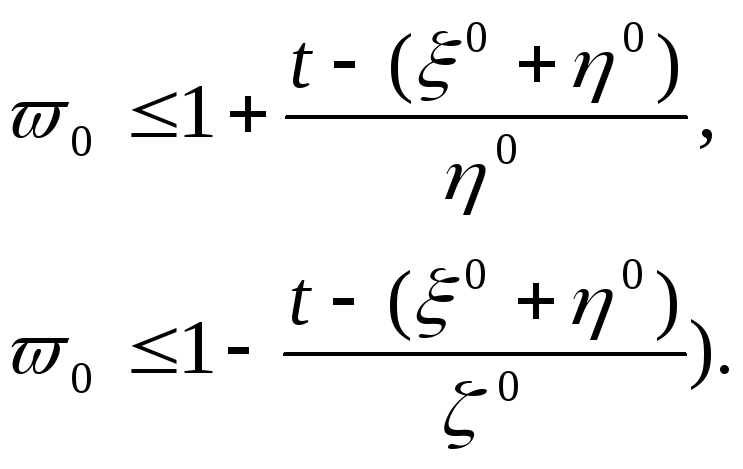
Рассмотрим модель
(2.2.1)-(2.2.2) в случае меры необходимости,
![]() .
Получаем модель следующего вида.
.
Получаем модель следующего вида.
![]() (2.2.13)
(2.2.13)
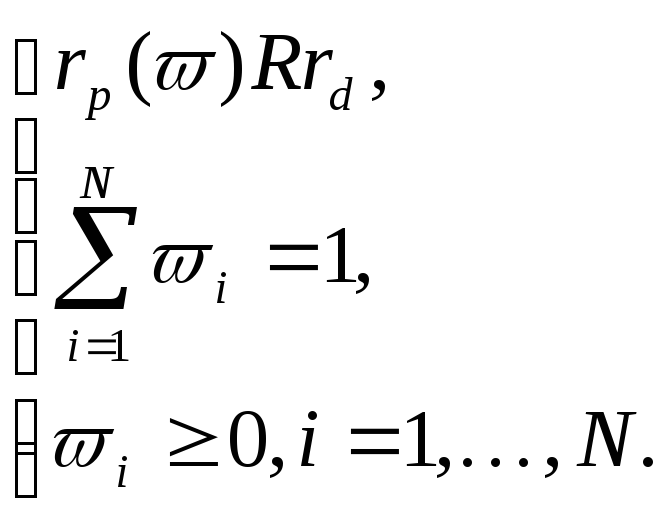 (2.2.14)
(2.2.14)
Докажем соответствующую теорему.
Теорема 2.2.2.
Пусть в задаче (2.2.13)-(2.2.14) возможностные
параметры
![]() ,
,![]() являются минисвязанными, тогда задача
(2.2.13)-(2.2.14) имеет эквивалентный
детерминированный аналог следующего
вида:
являются минисвязанными, тогда задача
(2.2.13)-(2.2.14) имеет эквивалентный
детерминированный аналог следующего
вида:
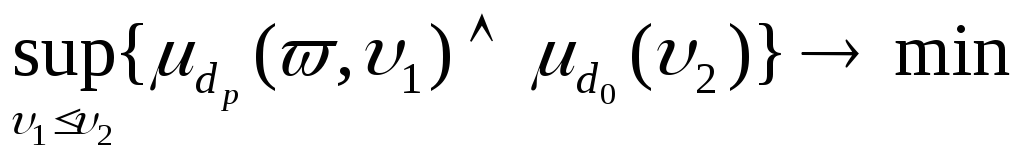 , (2.2.15)
, (2.2.15)
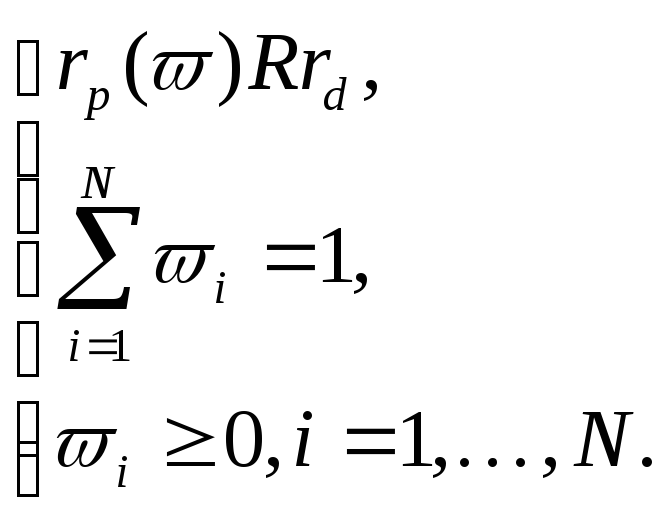 (2.2.16)
(2.2.16)
Доказательство.
Имеем.
![]() .
.
Следовательно модель (2.2.13) эквивалентна
![]() .
.
Если распределения
![]() и
и![]() непрерывны [91], то
непрерывны [91], то
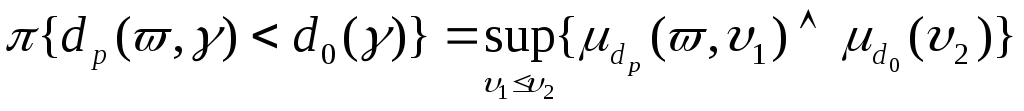
и эквивалентная модель критерия имеет вид
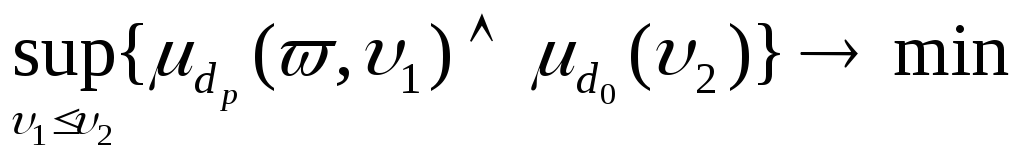 .
.
Таким образом, модель (2.2.13)-(2.2.14) имеет следующий эквивалентный детерминированный аналог.
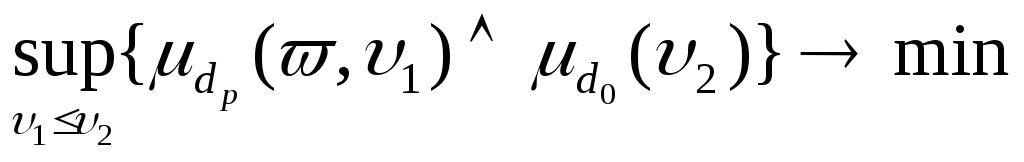 ,
,
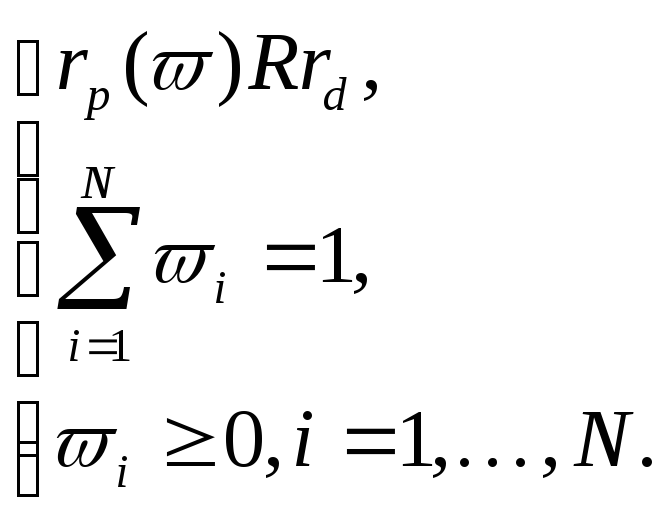
Теорема доказана.
Далее, преобразуя
выражение для дисперсии по уже известной
формуле (теорема 1.4.1), а также принимая
![]() ,
получаем:
,
получаем:
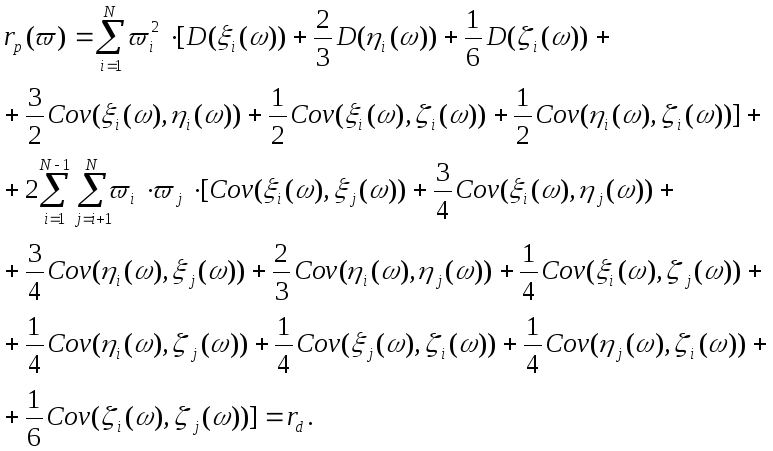
Если предположить, что параметры возможностного распределения являются независимыми случайными величинами, то
![]() .
.
Тогда наша задача будет иметь следующий вид.
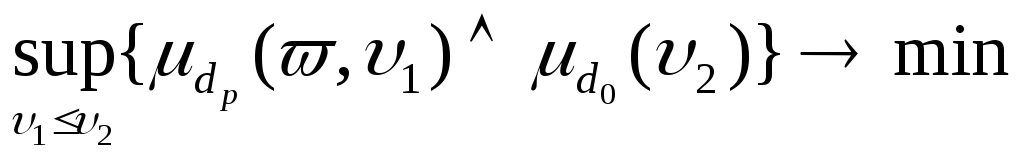 , (2.2.17)
, (2.2.17)
 (2.2.18)
(2.2.18)
