1. Развитие математической модели нечеткой случайной величины для решения задач портфельного анализа.

В первой главе диссертации развивается модель нечеткой случайной величины, разработанная в работе [72]. Основное внимание направлено на представление нечеткой случайной величины и разработку исчисления, позволяющего оценивать основные числовые характеристики нечеткой случайной величины: ожидаемое значение, коэффициенты ковариации и дисперсию.

1.1. Определение нечеткой случайной величины.

В настоящее время интенсивно развивается теория нечетких случайных величин и нечетких стохастических процессов. Она находит свое применение в таких научных областях, как математическая экономика, управление процессами и теория принятия решений [72].

Нечеткая случайная величина есть математическая модель случайного эксперимента с нечетким исходом [78,87,88]. Прежде, чем перейти к ее формальному определению, введем некоторые базовые понятия из теории возможностей [87].

Для начала введем некоторые необходимые определения [95].

Пусть есть множество элементов, обозначаемых через , - множество всех подмножеств , ­­- числовая прямая.

Определение 1.1.1. Мерой возможности называется функция множества , обладающая свойствами:

1. ,; 2.,

для любого индексного множества и множеств.

Триплет называется возможностным пространством.

Введем понятие меры необходимости, двойственной мере возможности.

Определение 1.1.2. Мерой необходимости называется функция множеств такая, что:

,

где есть мера возможности,,есть дополнение.

Обобщая результаты работ [86,89], можно дать следующее определение нечеткой величины и ее распределения.

Определение 1.1.3. Нечеткой (возможностной) величиной называется отображение . Распределением возможностных значений переменнойназывается функция, определяемая по правилу:

.

- есть возможность того, что переменная может принять значение.

Из определения и свойств возможностной меры следует, что

1. ; 2..

Определение 1.1.4. Носителем возможностной переменной называется множество.

Определение 1.1.5.Возможностная величинаназывается выпуклой, если ее распределение является квазивогнутым, то есть для любыхмы имеем

.

По аналогии с возможностной переменной можно ввести «необходимостную» переменную [95].

Определение 1.1.6. Необходимостной переменной называется отображение . Распределением необходимостных значений переменнойназывается функция, определяемая по правилу:

.

С другой стороны, из определения меры необходимости следует, что

.

Легко показать, что почти всегда равна нулю. Это несомненно в случае, когдане совпадает с модальным значением, что является скорее правилом, чем исключением, или еслинепрерывна. Следовательно, прямое применение формулы, определяющей необходимость, бесполезно. Однако необходимость можно рассматривать в контексте отношений между возможностными переменными.

На практике для моделирования нечетких параметров систем, как правило, используются классы параметризованных распределений. Приведем основные из них.

Определение 1.1.7. Нечеткая величина называется нормальной (обозначение класса ), если ее функция распределения имеет следующий вид:

,

где -модальное значение,-коэффициент нечеткости.

Определение 1.1.8. Нечеткая величина называется триангулярной (обозначение класса ), если ее функция распределения имеет следующий вид:

,

где -модальное значение,-коэффициент нечеткости.

Определение 1.1.9. Нечеткая величина называется трапецевидной (обозначение класса ), если ее функция распределения имеет следующий вид:

,

где -левый и правый коэффициенты нечеткости,-границы интервала толерантности.

Дадим понятие нечеткой величины типа [15].

Определение 1.1.10. Функциями представления формы или функциями называются числовые функции, которые определены и строго монотонны на неотрицательной части числовой прямой, полунепрерывны сверху и обладают свойствами:

1) ,

2) ,

3) .

Определение 1.1.11. Нечеткая величина называется нечеткой величинойтипа, если ее распределение имеет вид:

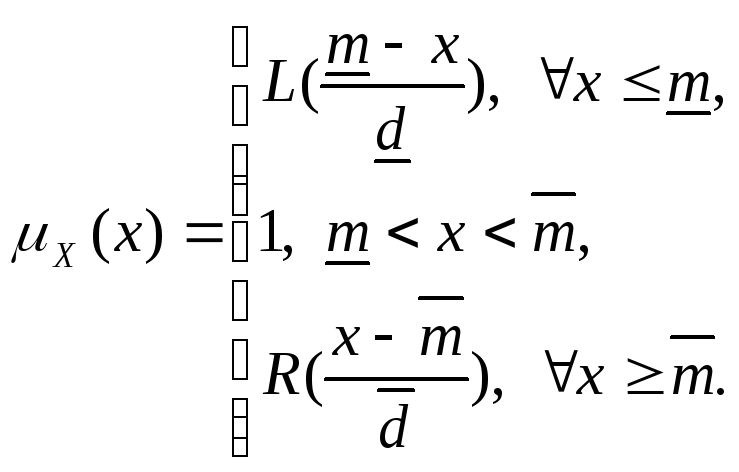
Здесь ,имеют смысл границ интервала толерантности нечеткой величины, а,есть левый и правый коэффициенты нечеткости соответственно. Тогда нечеткая величина может быть обозначена следующим образом.

Рассмотренные ранее нечеткие величины класса ,,могут быть отнесены к классу распределений-типа. Соответствующие функциииимеют следующий вид:

, для класса ;

, для классов ,.

В представленных классах возможностных распределений исчисление нечеткости осуществляется на параметрическом уровне. Имеют место следующие результаты.

Теорема 1.1.1.[86] Пусть минисвязанные нечеткие величины такие, что,. Тогда нечеткая величина.

Этот результат может быть обобщен на случай распределений -типа.

Теорема 1.1.2. Пусть минисвязанные нечеткие величины такие, что ,. Тогда нечеткая величина

.

Это следует из общих результатов теории возможностей [71]. Для детального изучения этого вопроса можно рекомендовать [71,95,24].

Нам необходима в дальнейшем также следующая лемма [94].

Введем функцию.

,

где иесть возможностные величины,,.

Определим рекуррентным способом следующую функцию

.

Следовательно,

.

Очевидно, что

.

Тогда имеет место лемма.

Лемма 1.1.1. Пусть возможностные величины являются минисвязанными. Тогда при фиксированном

.

Важным является понятие -уровневого множества возможностной величины.

Определение 1.1.12.Множествоназывается-уровневым множеством.

В контексте представленной структуры возможностного пространства и возможностной величины мы можем дать такое определение нечеткой случайной величины [95].

Пусть есть вероятностное пространство.

Определение 1.1.13. Нечеткая случайная величина есть вещественная функциятакая, что при любом фиксированном, величинаявляется случайной величиной на.

При фиксированном ,есть нечеткая величина, значения которой описываются возможностным распределением. При фиксированноместь случайная величина с возможностью, определяемой мерой возможности. Все сказанное становится более ясным, когда рассматриваемое распределениебудет определяться как в случае нечеткой переменной:

.

Теперь каждому отвечает возможностное распределение, представляющее случайный выбор эксперта, который дает неопределенную, субъективную оценку при определенном количестве. С другой стороны, фиксируя, имеем, чтоесть случайная величина, при этом мы не уверены в значении ее распределения.

Прежде чем определить моменты второго порядка введем определение -уровневого множества нечеткой случайной величины (при фиксированном).

Определение 1.1.14. -уровневым множеством нечеткой случайной величины называется множество .

Понятно, что границы определенного -уровневого множества являются случайными величинами: ,.

Возможностные величины, имеющие компактный носитель и характеризующиеся квазивогнутыми полунепрерывными сверху распределениями, будем называть нечеткими числами и обозначать этот класс нечетких величин через .

Для -уровневого множестваверны следующие утверждения [84].

Утверждение 1.1.1. Пусть . Тогда:

1) -замкнутый интервал,,

2) ,

3) .

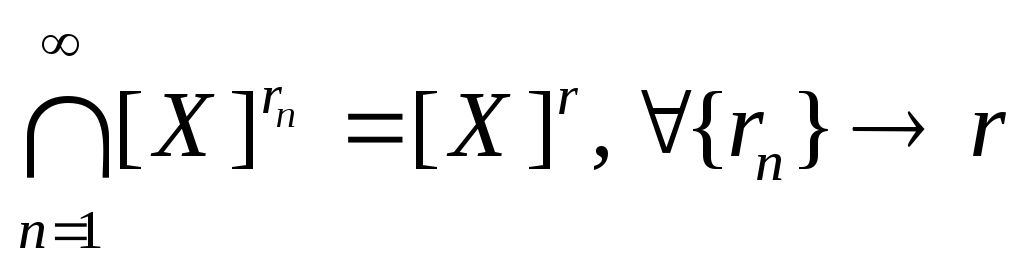Справедливо также следующее утверждение [84].

Утверждение 1.1.2. Если последовательность множеств удовлетворяет 1)-3) из Утверждения 1.1.1., то существует единственноетакое, что.

Согласно [84] имеет место следующая лемма.

Лемма 1.1.2. Для -уровневых множеств возможностных величиниопределены операции сложения и скалярного умножения:

1) ,

2) , .

Большое значение для дальнейших построений имеет следующая лемма [72,84].

Лемма 1.1.3. Пусть есть-уровневое множество, где,,являются верхней и нижней границами-уровневого множества. Тогда:

1) - неубывающая, непрерывная слева функция на,

2) - невозрастающая, непрерывная слева функция на,

3) .

Введем метрику в множестве .

Пусть .

Тогда

,

,

где -хаусдорфова метрика, т.е.

.

Необходимо отметить, что может быть бесконечным при, где.

Определим обобщенную норму возможностной величины [69].

Определение 1.1.15. Обобщенная норма нечеткого числаприопределяется следующим образом:

,

где .

Функция распределения принимает значение, равное единице, в нуле и нулю в остальных случаях.

Можно показать, что прии.

Доказано [72], что метрическое пространство не является полным для. Здесьесть множество всех нечетких чисел с компактным носителем в.

Введем определение двуместной функции, необходимой нам в дальнейшем [72].

Определение 1.1.16. Определим двуместную функцию 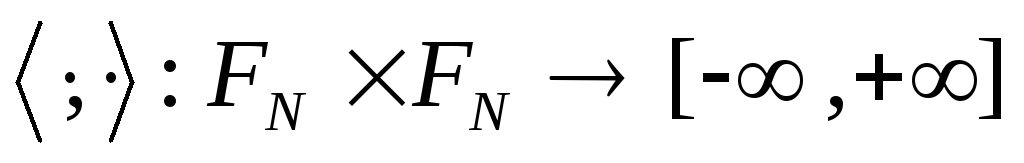по формуле:

.

Заметим, что если в интеграле Лебега возникает неопределенность вида , тоне существует.

Введенная функция обладает следующими свойствами, которые характеризуются теоремой [72].

Теорема 1.1.2. В условиях, определенных выше:

1) ,,

2) ,

3) ,

4) ,

5) , где.

Нетрудно видеть, что если является нечеткой случайной величиной, то-это случайное замкнутое интервальное множество и-вещественные случайные величины.

Определение 1.1.17.Нечеткая случайная величинаназывается ограниченно интегрируемой, если.

Определение 1.1.18.Ожидаемое значениеопределяется как единственное нечеткое число, удовлетворяющее условию

, если нечеткая случайная величина является ограниченно интегрируемой.

Перейдем к определению числовых характеристик нечетких случайных величин.