268 |
THE CRAIG INTERPOLATION THEOREM |
by γ . Let A(A ) be the conjunction of the members of T0 (T0 ). Then (1) is implied by
A & A Let c0, . . . , ck be constants not occurring in T T , and hence not in A, A ,
—α, x0, . . . , xk —, or —α , x0, . . . , xk —. Then
—α, c0, . . . , ck — ↔ —α , c0, . . . , ck —
is a consequence of (1) and therefore of A & A . Here of course by —α, c0, . . . , ck — is meant the result of substituting ci for xi in —α, x0, . . . , xk —for all i, and similarly for —α , c0, . . . , ck —. It follows that
|
(A & A ) → (—α, c0, . . . , ck — ↔ —α , c0, . . . , ck —) |
is valid, and hence that |
|
(4) |
A & —α, c0, . . . , ck — |
implies |
|
(5) |
A → —α , c0, . . . , ck —. |
We now apply the Craig interpolation lemma. It tells us that there is a sentence B(c0, . . . , ck ) implied by (4) and implying (5), such that the nonlogical symbols of B are common to (4) and (5). This means that they can include only the ci , which we have displayed, and the βi . Since (4) implies B(c0, . . . , ck ), A and therefore T implies
—α, c0, . . . , ck — → B(c0, . . . , ck )
and since the ci do not occur in T , this means T implies
(6) |
x0 · · · xk (—α, x0, . . . , xk — → B(x0, . . . , xk )). |
Since B(c0, . . . , ck ) implies (5), A and therefore T implies
B(c0, . . . , ck ) → —α , c0, . . . , ck —
and since the ci do not occur in T , this means T implies
|
x0 · · · xk (B(x0, . . . , xk ) → —α , x0, . . . , xk —). |
Replacing each symbol γ by γ , it follows that T implies |
|
(7) |
x0 · · · xk (B(x0, . . . , xk ) → —α, x0, . . . , xk —). |
But (6) and (7) together imply, and therefore T implies, the explicit definition
x0 · · · xk (—α, x0, . . . , xk — ↔ B(x0, . . . , xk )).
Thus, α is explicitly definable from the βi in T , and Beth’s theorem is proved.
Problems
20.1(Lyndon’s interpolation theorem) Let A and C be sentences without constants or function symbols and in negation-normal form. We say that an occurrence of a predicate in such a sentence is positive if it is not preceded by , and negative
PROBLEMS |
269 |
if it is preceded by . Show that if A implies C, and neither A nor C is valid, then there is another such sentence B such that: (i) A implies B; (ii) B implies C; (iii) any predicate occurs positively in B only if it occurs positively in both A and C, and occurs negatively in B if and only if it occurs negatively in both
Aand C.
20.2Give an example to show that Lyndon’s theorem does not hold if constants are present.
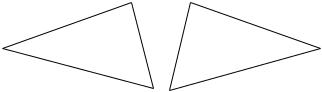
20.3(Kant’s theorem on the indefinability of chirality). For points in the plane, we say y is between x and z if the three points lie on a straight line and y is between x and z on that line. We say w and x and y and z are equidistant if the distance from w to x and the distance from y to z are the same. We say x and y and z form a right-handed triple if no two distances between different pairs of them are the same, and traversing the shortest side, then the middle side, then the longest side of the triangle having them as vertices takes one around the triangle clockwise, as on the right in Figure 20-1.
Figure 20-1. Right and left handed triangles.
Show that right-handedness cannot be defined in terms of betweenness and equidistance. (More formally, consider the language with a three-place predicate P, a four-place predicate Q, and a three-place predicate R; consider the interpretation whose domain is the set of the points in the plane and that assigns betweenness and equidistance and right-handedness as the denotations of P and Q and R; and finally consider the theory T whose theorems are all the sentences of the language that come out true under this interpretation. Show that R is not definable in terms of P and Q in this theory.)