
- •Contents
- •Preface to the Fifth Edition
- •1 Enumerability
- •1.1 Enumerability
- •1.2 Enumerable Sets
- •Problems
- •2 Diagonalization
- •Problems
- •3 Turing Computability
- •Problems
- •4 Uncomputability
- •4.1 The Halting Problem
- •4.2* The Productivity Function
- •Problems
- •5 Abacus Computability
- •5.1 Abacus Machines
- •5.2 Simulating Abacus Machines by Turing Machines
- •5.3 The Scope of Abacus Computability
- •Problems
- •6 Recursive Functions
- •6.1 Primitive Recursive Functions
- •6.2 Minimization
- •Problems
- •7 Recursive Sets and Relations
- •7.1 Recursive Relations
- •7.2 Semirecursive Relations
- •7.3* Further Examples
- •Problems
- •8.1 Coding Turing Computations
- •8.2 Universal Turing Machines
- •8.3∗ Recursively Enumerable Sets
- •Problems
- •9.1 First-Order Logic
- •9.2 Syntax
- •Problems
- •10.1 Semantics
- •10.2 Metalogical Notions
- •Problems
- •11 The Undecidability of First-Order Logic
- •11.1 Logic and Turing Machines
- •11.2 Logic and Primitive Recursive Functions
- •11.3 Lemma
- •Problems
- •12 Models
- •12.1 The Size and Number of Models
- •12.2 Equivalence Relations
- •Problems
- •13 The Existence of Models
- •13.1 Outline of the Proof
- •13.2 The First Stage of the Proof
- •13.3 The Second Stage of the Proof
- •13.4 The Third Stage of the Proof
- •13.5* Nonenumerable Languages
- •Problems
- •14 Proofs and Completeness
- •14.1 Sequent Calculus
- •14.2 Soundness and Completeness
- •14.3* Other Proof Procedures and Hilbert’s Thesis
- •Problems
- •15 Arithmetization
- •15.1 Arithmetization of Syntax
- •Problems
- •16 Representability of Recursive Functions
- •16.2 Minimal Arithmetic and Representability
- •16.3 Mathematical Induction
- •16.4* Robinson Arithmetic
- •Problems
- •17.1 The Diagonal Lemma and the Limitative Theorems
- •17.2 Undecidable Sentences
- •17.3* Undecidable Sentences without the Diagonal Lemma
- •Problems
- •18 The Unprovability of Consistency
- •Historical Remarks
- •19 Normal Forms
- •19.1 Disjunctive and Prenex Normal Forms
- •19.2 Skolem Normal Form
- •19.3 Herbrand’s Theorem
- •19.4 Eliminating Function Symbols and Identity
- •Problems
- •20 The Craig Interpolation Theorem
- •20.1 Craig’s Theorem and Its Proof
- •20.2 Robinson’s Joint Consistency Theorem
- •20.3 Beth’s Definability Theorem
- •Problems
- •21 Monadic and Dyadic Logic
- •21.1 Solvable and Unsolvable Decision Problems
- •21.2 Monadic Logic
- •21.3 Dyadic Logic
- •Problems
- •22 Second-Order Logic
- •Problems
- •23.2 Arithmetical Definability and Forcing
- •Problems
- •24 Decidability of Arithmetic without Multiplication
- •Problems
- •25 Nonstandard Models
- •25.1 Order in Nonstandard Models
- •25.2 Operations in Nonstandard Models
- •25.3 Nonstandard Models of Analysis
- •Problems
- •26 Ramsey’s Theorem
- •Problems
- •27 Modal Logic and Provability
- •27.1 Modal Logic
- •27.2 The Logic of Provability
- •27.3 The Fixed Point and Normal Form Theorems
- •Problems
- •Annotated Bibliography
- •General Reference Works
- •Textbooks and Monographs
- •By the Authors
- •Index
142 |
MODELS |
But this is simply the condition that j is one-to-one, which is part of the definition of being a correspondence, which in turn is part of the definition of being an isomorphism.
If function symbols are present, we must first prove as a preliminary that for any closed term t we have
(3) |
j(tP) = tQ. |
This is proved by induction on complexity of terms. For constants we have (3) by clause (I2) in the definition of isomorphism. And supposing (3) holds for t1, . . . , tn , then it holds for f (t1, . . . , tn ) since by clause (I3) in the definition of isomorphism we have
j(( f (t1, . . . , tn ))P) = j f P t1P, . . . , tnP
= f Q j t1P , . . . , j tnP = f Q t1Q, . . . , tnQ = ( f (t1, . . . , tn ))Q.
The proof given above for the atomic case of (1) now goes through even when the ti are complex closed terms rather than constants, and no further changes are required in the proof.
12.6 Corollary (Canonical-domains lemma).
(a)Any set of sentences that has a finite model has a model whose domain is the set {0, 1, 2, . . . , n} for some natural number n.
(b)Any set of sentences having a denumerable model has a model whose domain is the set {0, 1, 2, . . .} of natural numbers.
Proof: Immediate from Propositions 12.4 and 12.5.
Two models that are isomorphic are said to be of the same isomorphism type. The intelligent way to count the models of a given size that a sentence has is to count not literally the number of models (which is always a nonenumerable infinity if it is nonzero), but the number of isomorphism types of models. The import of the rather abstract results of this section should become clearer as they are illustrated concretely in the next section.
12.2 Equivalence Relations
Throughout this section we will work with a language whose only nonlogical symbol is a single two-place predicate ≡. We will write x ≡ y for what officially ought to be ≡(x, y). Our interest will be in models—and especially in denumerable models—of the following sentence Eq of the language:
x x ≡ x &
x y(x ≡ y → y ≡ x) &
x y z((x ≡ y & y ≡ z) → x ≡ z).
Such a model X will consist of a nonempty set X and a two-place relation ≡X or E on X. In order to make the three clauses of Eq true, E will have to have three properties.
12.2. EQUIVALENCE RELATIONS |
143 |
Namely, for all a, b, c in X we must have the following:
(E1) Reflexivity: a E a.
(E2) Symmetry: If a E b then b E a.
(E3) Transitivity: If a E b and b E c then a E c.
A relation with these properties is called an equivalence relation on X.
One way to get an equivalence relation on X is to start with what is called a partition of X . This is a set of nonempty subsets of X such that the following hold:
(P1) Disjointness: If A and B are in , then either A = B or A and B have no elements in common.
(P2) Exhaustiveness: Every a in X belongs to some A in .
The sets in are called the pieces of the partition.
Given a partition, define a E b to hold if a and b are in the same piece of the partition, that is, if, for some A in , a and b are both in A. Now by (P2), a is in some A in . To say a and a are ‘both’ in A is simply to say a is in A twice, and since it was true the first time, it will be true the second time also, showing that a E a, and that (E1) holds. If a E b, then a and b are both in some A in , and to say that b and a are both in A is to say the same thing in a different order, and is equally true, showing that b E a, and that (E2) holds. Finally, if a E b and b E c, then a and b are both in some A in and b and c are both in some B in . But by (P1), since A and B have the common element b, they are in fact the same, so a and c are both in A = B, and a E c, showing that (E3) holds. So E is an equivalence relation, called the equivalence relation induced by the partition.
Actually, this is in a sense the only way to get an equivalence relation: every equivalence relation is induced by a partition. For suppose E is any such relation; for any a in X let [a] be the equivalence class of a, the set of all b in X such that a E b; and let be the set of all these equivalence classes. We claim is a partition. Certainly any element a of X is in some A in , namely, a is in [a], by (E1). So (P2) holds. As for (P1), if [a] and [b] have a common element c, we have a E c and b E c, and having b E c, by (E2) we have also c E b, and then, having a E c and c E b, by (E3) we have also a E b, and by (E2) again we have also b E a. But then if d is any element of [a], having a E d and b E a, by (E3) again we have b E d, and d is in [b]. In exactly the same way, any element of [b] is in [a], and [a] = [b]. So is a partition, as claimed. We also claim the original E is just the equivalence relation induced by this partition . For along the way we have shown that if a E b then a and b belong to the same piece [a] = [b] of the partition, while of course if b belongs to the same piece [a] of the partition that a does, then we have a E b, so E is the equivalence relation induced by this partition.
We can draw a picture of a denumerable model of Eq, by drawing dots to represent elements of X with boxes around those that are in the same equivalence class. We can also describe such a model by describing its signature, the infinite sequence of numbers whose 0th entry is the number (which may be 0, 1, 2, . . . , or infinite) of equivalence classes having infinitely many elements and whose nth entry for n > 0 is
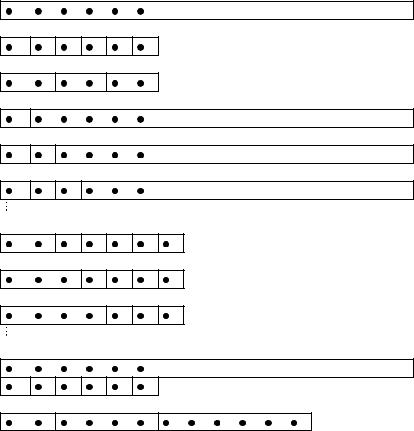
144 |
MODELS |
the number of equivalence classes with exactly n elements. The examples to follow are illustrated by pictures for equivalence relations of a variety of different signatures in Figure 12-1.
(a) Signature (1, 0, 0, 0, 0, … )
…
(b) Signature (0, ∞, 0, 0, 0, … )
…
(c) Signature (0, 0, ∞, 0, 0, … )
…
(d)(i) Signatures (1, 1, 0, 0, 0, … ), (1, 2, 0, 0, 0, … ), (1, 3, 0, 0, 0, … ), and so on
…
…
…
(d)(ii) Signatures (0, ∞, 1, 0, 0, … ), (0, ∞, 0, 1, 0, …), (0, ∞, 0, 0, 1, … ) and so on
…
…
…
(d)(iii) Signature (1, ∞, 0, 0, 0, … )
…
…
(e) Signature (0, 0, 1, 0, 1, 0, 1, 0, … )
…
Figure 12-1. Equivalence relations.
12.7 Example (A promiscuous model). Let a be the set containing Eq and the following sentence Ea :
x y x ≡ y.
A denumerable model of a consists of a denumerable set X with an equivalence relation E in which all elements are in the same equivalence class, as in Figure 12-1(a). We claim all such models are isomorphic. Indeed, if
X = {a1, a2, a3, . . .} and Y = {b1, b2, b3, . . .}
are any two denumerable sets, if X is the model with domain X and ≡X the relation that holds among all pairs ai , a j of elements of X, and if Y is the model with domain Y and ≡Y the relation that holds among all pairs bi , b j of elements of Y , then the function sending ai to
12.2. EQUIVALENCE RELATIONS |
145 |
bi is an isomorphism between X and Y. Condition (I1) in the definition of isomorphism—
the only applicable condition—says that we must in all cases have ai |
≡X a j |
if and only if |
f (ai ) ≡Y f (a j ); and of course we do, since we always have both ai |
≡X a j |
and bi ≡Yb j . |
Thus a has only one isomorphism type of denumerable model. |
|
|
12.8 Example (An eremitic model). Let b be the set containing Eq and the following sentence Eb:
x y (x ≡ y ↔ x = y).
A denumerable model of b consists of a denumerable set X with an equivalence relation E in which each element is equivalent only to itself, so each equivalence class consists of but a single element, as in Figure 12-1(b). Again any two such models are isomorphic. With the notation as in the preceding example, this time we have ai ≡X a j if and only if f (ai ) ≡Y f (a j ), because we only have ai ≡X a j when i = j, which is precisely when we have bi ≡Y b j .
12.9Example (Two isomorphism types). Let ab be the set containing Eq and the disjunction Ea Eb. Any model of ab must be either a model of a or one of b, and all models of either are models of ab. Now all denumerable models of a are isomorphic to each other, and all denumerable models of b are isomorphic to each other. But a model ofa cannot be isomorphic to a model of b, by the isomorphism lemma, since Ea is true in the former and false in the latter, and inversely for Eb. So ab has exactly two isomorphism types of denumerable model.
12.10Example (An uxorious model). Let c be the set containing Eq and the following sentence Ec:
x y(x = y & x ≡ y & z(z ≡ x → (z = x z = y))).
A denumerable model of c consists of a denumerable set X with an equivalence relation E in which each element is equivalent to just one other element than itself, so each equivalence class consists of exactly two elements, as in Figure 12-1(c). Again there is only one isomorphism type of denumerable model. If we renumber the elements of X so that a2 is the equivalent of a1, a4 of a3, and so on, and if we similarly renumber the elements of Y , again the function f (ai ) = bi will be an isomorphism.
12.11Example (Three isomorphism types). Let abc be the set containing Eq and the disjunction Ea Eb Ec. Then abc has three isomorphism types of denumerable models. The reader will see the pattern emerging: we can get an example with n isomorphism types of denumerable models for any positive integer n.
12.12Example (Denumerably many isomorphism types). Let d be the set containing Eq and the following sentence Ed :
x y(( u(u = x & u ≡ x) & v(v = y & v ≡ y)) → x ≡ y).
A denumerable model of d will consist of a denumerable set X with an equivalence relation in which any two elements a and b that are not isolated, that is, that are such that each is equivalent to something other than itself, are equivalent to each other. Here there are a number of possible pictures. It could be that all elements are equivalent, or that all
146 MODELS
elements are isolated, as in Figure 12-1(a) or (b). It could also be the case that there is one isolated element with all the other elements being equivalent. Or there could be two isolated elements with all the other elements being equivalent. Or three, and so on, as in Figure 12-1(d)(i).
There are further possibilities. For, supposing there are infinitely many isolated elements, the remaining equivalence class, consisting of all nonisolated elements, may contain two or three or . . . elements, as in Figure 12-1(d)(ii)—or it could contain zero, but that is Figure 12-1(b) again. Finally there is the possibility (whose picture takes two lines to draw) of infinitely many isolated elements plus an infinite class of other elements, all equivalent to each other, as in Figure 12-1(d)(iii).
Any two models corresponding to the same picture (or, what comes to the same thing, the same signature) are isomorphic. If there are only n isolated elements, renumber so that these are a1 through an . If there are only n nonisolated elements, renumber so that these are a1 through an instead. And if there are infinitely many of each, renumber so that a1, a3, a5, . . . are the isolated ones, and a2, a4, a6, . . . the nonisolated ones. Renumber the bi similarly, and then, as always, the function f (ai ) = bi can be checked to be an isomorphism. No two models corresponding to different pictures are isomorphic, for if a is nonisolated, a satisfies the formula
y(y = x & y ≡ x).
So by the isomorphism lemma, if f is an isomorphism, f (a) must also satisfy this formula, and so must be nonisolated. And for the same reason, applied to the negation of this formula, if a is isolated, f (a) must be isolated. So an isomorphism must carry nonisolated to nonisolated and isolated to isolated elements, and the numbers of nonisolated and of isolated elements must be the same in both models. Here, then, is an example where there are denumerably many of isomorphism types of denumerable models.
12.13 Example (Nonenumerably many isomorphism types). The sentence Eq all by itself has nonenumerably many isomorphism types of denumerable models. For any infinite set of positive integers S there is a model in which there is exactly one equivalence class with exactly n elements for each n in S, and no equivalence class with exactly n elements for any n not in S. For instance, if S is the set of even numbers, the model will look like Figure 12-1(e). We leave it to the reader to show how the isomorphism lemma can be used to show that no two models corresponding to different sets S are isomorphic. Since there are nonenumerably many such sets, there are nonenumerably many isomorphism types of models.
12.3 The L¨owenheim–Skolem and Compactness Theorems
We have seen that there are sentences that have only infinite models. One might wonder whether there are sentences that have only nonenumerable models. We have also seen that there are enumerable sets of sentences that have only infinite models, though every finite subset has a finite model. One might wonder whether there are sets of sentences that have no models at all, though every finite subset has a model. The answer to both these questions is negative, according to the following pair of theorems. They are basic results in the theory of models, with many implications about the existence, size, and number of models.
12.3. THE L OWENHEIM¨ |
–SKOLEM AND COMPACTNESS THEOREMS |
147 |
12.14Theorem (Lowenheim¨ –Skolem theorem). If a set of sentences has a model, then it has an enumerable model.
12.15Theorem (Compactness theorem). If every finite subset of a set of sentences has a model, then the whole set has a model.
We explore a few of the implications of these theorems in the problems at the end this chapter. We stop here just to note three immediate implications.
12.16 Corollary (Overspill principle). If a set of sentences has arbitrarily large finite models, then it has a denumerable model.
Proof: Let be a set of sentences having arbitrarily large finite models, and for each m let Im be the sentence with identity but no nonlogical symbols considered in Example 12.1, which is true in a model if and only if the model has size ≥ m. Let
* = {I1, I2, I3, . . . }
be the result of adding all the Im to . Any finite subset of * is a subset of {I1, I2, . . . , Im } for some m, and since has a model of size ≥ m, such a set has a model. By the compactness theorem, therefore, * has a model. Such a model is of course a model of , and being also a model of each Im , it has size ≥ m for all finite m, and so is infinite. By the Lowenheim¨ –Skolem theorem, we could take it to be enumerable.
A set of sentences is (implicationally) complete if for every sentence A in its language, either A or A is a consequence of , and denumerably categorical if any two denumerable models of are isomorphic.
12.17 Corollary (Vaught’s test). If is a denumerably categorical set of sentences having no finite models, then is complete.
Proof: Suppose is not complete, and let A be some sentence in its language such that neither A nor A is a consequence of . Then both { A} and { A} are satisfiable, and by the Lowenheim¨ –Skolem theorem they have enumerable models P− and P+. Since has no finite models, P− and P+ must be denumerable. Since is denumerably categorical, they must be isomorphic. But by the isomorphism lemma, since A is untrue in one and true in the other, they cannot be isomorphic. So the assumption that is not complete leads to a contradiction, and must be complete after all.
Thus if is any of the examples of the preceding section in which we found there was only one isomorphism type of denumerable model, then adding the sentences I1, I2, I3, . . . to (in order to eliminate the possibility of finite models) produces an example that is complete.
The Lowenheim¨ –Skolem theorem also permits a sharpening of the statement of the canonical-domains lemma (Lemma 12.6).
12.18 Corollary (Canonical-domains theorem).
(a)Any set of sentences that has a model, has a model whose domain is either the set of natural numbers < n for some positive n, or else the set of all natural numbers.
148 |
MODELS |
(b)Any set of sentences not involving function symbols or identity that has a model, has a model whose domain is the set of all natural numbers.
Proof: (a) is immediate from the Lowenheim¨ –Skolem theorem and Corollary 12.6. For (b), given a set of sentences not involving function symbols or identity, ifhas a model, apply part (a) to get, at worst, a model Y with domain the finite set {0, 1, . . . , n − 1} for some n. Let f be the function from the set of all natural numbers to this finite set given by f (m) = min(m, n − 1). Define an interpretation X with domain the set of all natural numbers by assigning to each k-place relation symbol R as denotation the relation RX that holds for p1, . . . , pk if and only if RY holds for f ( p1), . . . , f ( pk ). Then f has all the properties of an isomorphism except for not being one-to-one. Examining the proof of the isomorphism lemma (Proposition 12.5), which tells us the same sentences are true in isomorphic interpretations, we see that the property of being one-to-one was used only in connection with sentences involving identity. Since the sentences in do not involve identity, they will be true in X because they are true in Y.
The remainder of this section is devoted to an advance description of what will be done in the following two chapters, which contain proofs of the Lowenheim¨ –Skolem and compactness theorems and a related result. Our preview is intended to enable the readers who are familiar with the contents of an introductory textbook to decide how much of this material they need or want to read. The next chapter, Chapter 13, is devoted to a proof of the compactness theorem. Actually, the proof shows that if every finite subset of a set has a model, then has an enumerable model. This version of the compactness theorem implies the Lowenheim¨ –Skolem theorem, since if a set has a model, so does every subset, and in particular every finite subset. An optional final section 13.5 considers what happens if we admit nonenumerable languages. (It turns out that the compactness theorem still holds, but the ‘downward’ Lowenheim¨ –Skolem theorem fails, and one gets instead an ‘upward’ theorem to the effect that any set of sentences having an infinite model has a nonenumerable model.)
Every introductory textbook introduces some notion of a deduction of a sentence D from a finite set of sentences . The sentence D is defined to be deducible from a finite set if and only if there is a deduction of the sentence from the set. A deduction from a subset of a set always counts as a deduction from that set itself, and a sentence D is defined to be deducible from an infinite set if and only if it is deducible from some finite subset. A sentence D is defined to be demonstrable if it is deducible from the empty set of sentences , and a set of sentences is defined to be inconsistent if the constant false sentence is deducible from it. The better introductory textbooks include proofs of the soundness theorem, according to which if D is deducible from , then D is a consequence of (from which it follows that if D is demonstrable, then D is valid, and that if is inconsistent, then is unsatisfiable), and of the Godel¨ completeness theorem, according to which, conversely, if D is a consequence of , then D is deducible from (from which it follows that if D is valid, then D is demonstrable, and that if is unsatisfiable, then is inconsistent). Since by definition a set is consistent if and only if every finite subset is, it follows that a set is satisfiable if and only if every finite subset is: the compactness theorem follows from the soundness and completeness theorems. Actually, the proof
