|
Пусть |
однозначная |
функция |
w = f (z) |
определена |
в |
некоторой |
|||||
окрестности |
точки z, |
включая |
и |
саму |
точку. |
Тогда предел |
||||||
|
∆w |
|
|
f (z + ∆z) − f (z) |
′ |
если |
он |
существует, |
называется |
|||
lim |
|
= lim |
|
|
|
= f (z), |
||||||
∆z |
|
∆z |
||||||||||
∆z→0 |
∆z→0 |
|
|
|
|
|
|
|
||||
производной функции |
f(z) точке z, а функция f(z) |
называется |
||||||||||
дифференцируемой в точке z. |
|
|
|
|
|
|
||||||
|
Однозначная функция f (z) |
называется аналитической (голоморфной) в |
||||||||||
точке z, если она дифференцируема в некоторой окрестности этой точки. Функция f (z) называется аналитической в области D, если она
дифференцируема в каждой точке z D .
8.11 СЛУЧАЙНЫЕ СОБЫТИЯ
Событием называется факт, который в опыте может произойти или не произойти. События обычно обозначаются заглавными буквами латинского
алфавита, например, A, B, H1 .
Если событие обязательно появляется в результате данного опыта, то оно называется достоверным, и будем обозначать его буквой U (его также называют множеством допустимых исходов).
Если событие заведомо не может произойти в результате опыта, то оно называется невозможным, и будем обозначать его как V .
Произведением (пересечением) событий A и B (обозначается A B
или A ∩ B) называется событие C , которое происходит тогда и только тогда, когда происходят события A и B.
События A и B называются несовместными, если не могут появиться одновременно в одном опыте, т.е. A B =V .
Суммой (объединением) событий A и B (обозначается A + B или A B) называется событие C , которое происходит тогда, когда происходит событие A, либо B, либо оба вместе.
Событие A называется противоположным (дополнением) к событию
A, если оно происходит тогда и только тогда, когда не происходит событие
A.
Событие A влечет (принадлежит) событие B (обозначается A B), если при наступлении события A обязательно наступает событие B.
Для описания степени возможности появления события A в опыте вводится числовая функция P(A), называемая вероятностью, которая
удовлетворяет трем аксиомам:
1)P(A) ≥ 0 – аксиома неотрицательности;
2)P(U ) =1 – аксиома нормированности;
3)P(A + B) = P(A) + P(B), если A и B несовместные – аксиома
сложения.
Вероятность обладает следующими свойствами:
•P(V ) = 0;
•0 ≤ P(A) ≤1;
•P(A) =1− P(A);
•если A B, значит, P(A) ≤ P(B) .
Вопыте с равновозможными случайными исходами вероятность события A вычисляется как отношение числа исходов M , благоприятных событию A, к общему числу N всех возможных исходов (классическое определение вероятности):
P(A) = M / N .
Перестановкой из n элементов называется любой упорядоченный набор этих элементов. Число перестановок обозначается Pn и вычисляется по
формуле Pn = n!.
Размещением из n элементов по m называется любой упорядоченный набор m элементов, выбранных из совокупности n элементов. Число
размещений обозначается Am и вычисляется по формуле Am = |
n! |
|
. |
||
(n − m)! |
|||||
n |
n |
|
|||
Сочетанием из n |
элементов по m называется любой |
||||
неупорядоченный набор m элементов, выбранных из совокупности n элементов. Число сочетаний обозначается Cnm и вычисляется по формуле
Cnm = |
n! |
|
. |
|
m!(n − m)! |
||||
|
|
|||
Если число равновозможных исходов несчетно и представляет собой некоторое непрерывное множество, то реализуется принцип геометрической вероятности. В данном случае опыт заключается в бросании точки в пределах множества допустимых исходов – области Ω. Тогда вероятность попадания точки в н екоторое подмножество – область A – находится по формуле
P(A) = µ(A) / µ(Ω),
где µ – мера области в зависимости от ее размерности (длина, площадь, объем и
т.д.).
Для нахождения вероятности одновременного наступления событий A
и B используется формула умножения вероятностей
P(A B) = P(A) P(B | A) = P(B) P(A | B) ,
где P(B | A) – условная вероятность события B при условии, что событие A произошло (аналогично определяется P(A | B) ).
Если события A и B независимы, т.е. наступление одного события не влияет на вероятность появления другого, то P(A B) = P(A) P(B).
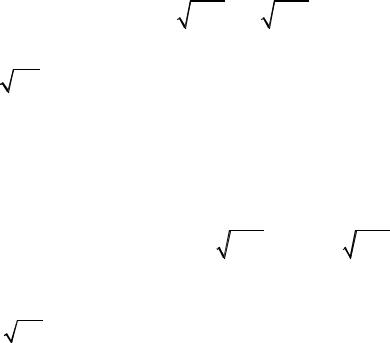
Пусть событие A может наступить только при появлении одного из событий H1 , H2 ,…, Hn , которые образуют полную группу – события H1 ,
|
|
|
|
|
|
n |
H2 ,…, Hn |
попарно несовместны |
друг |
с другом |
и |
∑P(Hi ) =1. Тогда |
|
|
|
|
A |
|
|
i=1 |
вероятность |
наступления |
события |
вычисляется |
по формуле полной |
||
вероятности |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
P(A) = ∑P(Hi ) P(A | Hi ), |
|
||||
|
|
i=1 |
|
|
|
|
причем H1 , H2 ,…, Hn называют гипотезами. |
|
|
||||
Пусть производится |
n независимых опытов, |
в каждом из которых |
||||
событие A может появиться с одной и той же вероятностью p (вероятность
«успеха»). При этом q =1− p называют вероятностью «неудачи», и такая последовательность опытов называется схемой Бернулли. Тогда вероятность
того, что в n опытах событие |
A появится m раз, вычисляется по формуле |
|||||||||||||||
Бернулли |
|
|
|
|
|
P |
(m) = Cm pmqn−m . |
|||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
n |
|
|
|
Теорема Пуассона. Пусть в схеме Бернулли n велико, а p близко к 0, |
||||||||||||||||
тогда |
|
|
|
|
|
|
λm |
|
|
|
|
|
||||
|
|
|
|
|
|
P (m) |
≈ |
e−λ , где λ = np . |
||||||||
|
|
|
|
|
|
n |
|
|
m! |
|
|
|
|
|
||
Локальная теорема Муавра-Лапласа. Пусть в схеме Бернулли n |
||||||||||||||||
велико, а p и q не близки к 0, тогда |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
P (m) ≈ |
|
|
1 |
|
m − np |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
ϕ |
|
, |
||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
n |
|
|
|
|
npq |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
npq |
|||
где ϕ(x) = |
|
1 |
|
e− |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
. |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2π |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Интегральная теорема Муавра-Лапласа. Пусть в схеме Бернулли n
велико, а p и q не близки к 0. Тогда вероятность того, что число успехов m
будет заключено в пределах от m1 |
до m2 |
можно найти по приближенной |
|||||||||||||||
формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m − np |
m − np |
|
|||||||
|
|
P{m |
< m < m |
}≈ Φ |
2 |
|
|
|
−Φ |
1 |
|
|
, |
||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
1 |
2 |
|
|
npq |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
npq |
|
||
|
|
1 |
|
x |
|
y2 |
|
|
|
|
|
|
|
|
|
|
|
где Φ(x) = |
|
|
∫e− |
|
dy . |
|
|
|
|
|
|
|
|
|
|
||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2π |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
8.12 СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Случайной величиной называется числовая функция, которая каждому исходу опыта ставит в соответствие некоторое число. Случайные величины обозначаются как греческими буквами ξ , η, так и латинскими X , Y , при
этом значения случайной величины будем обозначать через x , y . Случайная величина ξ характеризуется функцией распределения
F (x), которая в каждой точке x определяется как вероятность события
{ξ < x}, т.е. F (x)= P{ξ < x}. |
Функция распределения удовлетворяет |
|
следующим свойствам: |
|
|
• |
0 ≤ F(x) ≤1; |
|
• |
F (x) – неубывающая функция; |
|
• |
F (−∞)= lim F(x) = 0, F (+∞)= lim F(x) =1; |
|
|
x→−∞ |
x→+∞ |
•вероятность попадания случайной величины ξ в интервал [x1, x2 ) находится по формуле P{x1 ≤ξ < x2}= F (x2 )− F (x1 ).
Случайная величина называется дискретной, если ее значения представляют собой конечный (или счетный) набор чисел.
Дискретная случайная величина ξ описывается законом распределения в виде следующей таблицы
|
ξ |
x1 |
x2 |
|
|
… |
xn |
|
|
P |
p1 |
p2 |
|
|
… |
pn |
|
В первой строке в возрастающем порядке |
расположены все возможные |
|||||||
значения случайной величины, а во второй |
– вероятности, что случайная |
|||||||
величина примет то или иное значение: |
pi = P{ξ = xi }, i =1,2,...,n . |
|||||||
Математическое ожидание дискретной случайной величины ξ
характеризует среднее значение случайной величины и определяется по формуле
n
Mξ = ∑xi pi .
i=1
Математическое ожидание удовлетворяет следующим свойствам:
•если c = const , то Mc = c ;
•если a и b = const , то M (aξ +b)= aMξ +b .
Дисперсия дискретной случайной величины ξ характеризует меру
разброса случайной величины относительно математического ожидания и определяется по формуле
n
Dξ = ∑(xi − Mξ)2 pi .
i=1
Дисперсия удовлетворяет следующим свойствам:
•если c = const , то Dc = 0;
•если a и b = const , то D(aξ +b)= a2 Dξ ;
•Dξ ≥ 0;
•удобная формула вычисления дисперсии – Dξ = Mξ2 −(Mξ)2 .
Иногда для описания разброса случайной величины используется
среднеквадратическое отклонение, определяемое как σξ = 
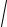Dξ .
Биноминальное распределение имеет случайная величина ξ – число успехов в n испытаниях по схеме Бернулли, где вероятность находится по
формуле |
Бернулли: |
P{ξ = k}= Cnk pk qn−k , |
k = 0,1,...,n. |
Для |
|||
биноминального закона |
известны числовые характеристики |
Mξ = np |
и |
||||
Dξ = npq . |
|
|
|
|
|
|
|
Распределение Пуассона имеет случайная величина η – число успехов |
|||||||
в схеме Бернулли, |
где вероятность находится по |
формуле Пуассона |
|||||
P{η = k}= |
λk e−λ , |
k = 0,1,... и λ > 0 – параметр распределения Пуассона. |
|||||
|
k! |
|
|
|
Mη = λ |
|
|
Для закона |
Пуассона |
известны числовые характеристики |
и |
||||
Dη = λ.
Геометрическое распределение имеет случайная величина µ – число испытаний в схеме Бернулли до наступления «успеха». Вероятность находится по формуле: P{µ = k}= pqk , k = 0,1,..., и числовые
характеристики M µ = q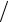
p и Dµ = q
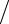p2 .
Случайная величина называется непрерывной, если ее значения непрерывно заполняют некоторый интервал с плотностью распределения
f (x), связанной с функцией распределения по формуле f (x)= F′(x), и
наоборот F (x)= ∫x f (y)dy . Плотность распределения удовлетворяет
−∞
следующим свойствам:
•f (x)≥ 0;
• вероятность попадания случайной величины ξ в интервал [x1, x2 )
x2
можно найти по формуле P{x1 ≤ξ < x2}= ∫ f (x)dx ;
x1