umm_465

Зависимость (3.21) выражает равенство условных рисков ошибочных решений.

Метод наибольшего правдоподобия дает решение, не требующее знания точных значений стоимости ошибок и вероятностей состояния, а только качественно отражающее их соотношение. Тогда правило решения принимается следующим:

т. е., граничное значение находится в точке пересечения кривых плотностей вероятностей из условия

Условие (3.21) можно использовать, когда заранее известно, что

С12>> С21; Р1>> Р2 .

В условиях работы подвижного состава бывает очень сложно дать количественную оценку последствий пропуска дефекта. Например, в нашем примере дефект буксового подшипника вагона может привести к задержке поезда (браку в работе), к аварии, последствия которой более тяжелые, и, наконец, к крушению поезда, последствия которого могут быть катастрофическими.

Вто же время ложная тревога поддается более точной оценке потерь, связанных в нашем случае с обнаружением ошибки в принятии решения. Более того, можно определить допустимый уровень частоты появления ложной тревоги, не влияющий существенно на работу транспорта в целом.

Вданном случае полезно использовать метод Неймана-Пирсона, в соответствии с которым минимизируется вероятность пропуска цели (дефекта). Если задан максимально допустимый уровень вероятности ложной тревоги L, то условием наименьшей вероятности пропуска дефекта будет

20

Условие (3.24) однозначно определяет величину xо для заданного уровня вероятности ложной тревоги L. В ряде случаев можно исходить из заданного значения вероятности пропуска дефекта F и минимизировать вероятность ложной тревоги:

−∞

В нашем примере значение L зависит от конкретных условий эксплуатации. Приборы обнаружения перегретых букс располагаются, как правило, перед станцией не менее чем за 3 км от входного сигнала с тем, чтобы в случае обнаружения опасного перегрева была возможность остановить поезд на станции и снизить скорость перед въездом на стрелки до 20 км/ч, применяя при этом только служебное регулировочное торможение.

Цена ложной тревоги зависит от того, перед какой станцией расположен прибор. Если прибор расположен перед участковой станцией, на которой не предусмотрена графиком остановка поезда, то цена ложной тревоги высока, более того, в случае частых задержек поездов движение на участке может быть парализовано. Если прибор расположен перед сортировочной станцией, где предусмотрено техническое обслуживание вагонов и имеется достаточное путевое развитие, а также имеется механизированный пункт текущего ремонта, цена ложной тревоги мала и связана в основном с контрольной проверкой показаний аппаратуры.

Поэтому в практике эксплуатации приборов обнаружения перегретых букс для каждой станции устанавливается уровень порога температуры с учетом конкретных условий.

Вопросы для самоподготовки:

1.Как определить вероятность пропуска дефекта?

2.Как определить вероятность ложной тревоги?

3.Что необходимо знать, для принятия решения с минимальным риском?

4.В каких случаях целесообразно использовать метод Неймана-Пирсона?

5.В чем сущность метода минимакса?

6.Какой метод следует применить, когда нет данных о цене ошибок?

7.В каких случаях пользуются методом наибольшего правдоподобия?

8.В каких случаях целесообразно использовать метод минимального числа ошибочных решений?

9.Что определяет отношение правдоподобия?

21

4. ДИАГНОСТИЧЕСКАЯ ИНФОРМАЦИЯ

4.1. Оценка количества диагностической информации

Средства технического диагностирования (СТД) предназначены для получения информации о техническом состоянии объекта и основной характеристикой СТД является объем или количество получаемой информации.

Диагностическими параметрами называются элементы множества параметров объекта, содержащие информацию о неисправностях, над которыми установлены наблюдение и контроль. Существует различие между множествами параметров объекта и диагностическими параметрами. В отличие от параметров, образующих множество выходных величин, состав которых обычно не определен и не постоянен, на множество диагностических параметров накладываются дополнительные ограничения: эти параметры должны быть достаточно

информативными и, кроме того, доступными для измерения или наблюдения.

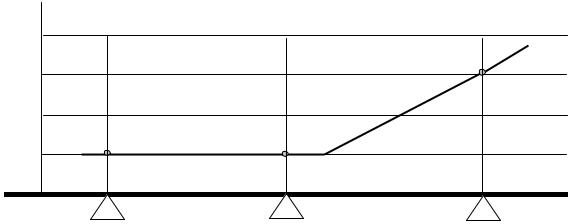
Начнем с нашего примера. При следовании поезда он проходит с установленной скоростью N постов контроля перегрева букс К, как показано на рис. 4.1. На посту контроля КN от датчика перегрева корпуса буксы поступило сообщение о перегреве одной из букс в проходящем поезде на θN = 30°C. Такой уровень перегрева допустим для участковой станции, но является пороговым перед ПТО сортировочной станции (по методу Неймана-Пирсона).

L

Рис. 4.1. Диаграмма перегрева корпуса буксы при следовании поезда

В то же время поступило второе сообщение о сравнении измеренной

температуры с температурой этой же буксы θN-1= θN-2 =10°C при прохождении предыдущих постов контроля КN-1 и КN-2, в результате зарегистрирован

прирост температуры перегрева на Δθ = +20°C.

Рассмотрим, какое из этих сообщений несет больше диагностической информации. Как мы уже убедились ранее, вероятность правильного решения на

22

основании данных о перегреве корпуса буксы на θ = 30°C равна 0,72. Второе сообщение определяет не только о вероятность наличия дефекта в буксовом подшипнике, но и однозначно свидетельствует о его интенсивном развитии и невозможности дальнейшего следования поезда. По второму сообщению можем принимать вероятность наличия опасного дефекта, близкую 1, например, равную 0,99.

Очевидно, что второе сообщение несет больше информации, так как практически полностью устраняет неопределенность состояния объекта. На основании этого можно утверждать, что величина информации – это разность неопределенностей (энтропий) системы до и после получения информации. Дадим некоторые определения.

Информация - совокупность сведений об объекте, рассматриваемая с позиций передачи этих сведений в пространстве и во времени.

Сообщение - это информация, выраженная в определенной форме и предназначенная для передачи от источника к пользователю (тексты, фото, речь, музыка, телевизионное изображение и др.).

Сигнал - это физический процесс, распространяющийся в пространстве и времени, параметры которого способны отображать (содержать) сообщение.

Рассмотрим понятие энтропии статистической системы. В общем случае энтропия характеризует состояния и возможные изменения состояний материальных систем, в термодинамике – тепловое состояние вещества. Теория информации возникла с развитием технических средств связи и изучает методы передачи сообщений как связь статистических систем. Передача какого-либо сообщения, состоящего из последовательности элементов, это случайный процесс, так как получатель может ожидать любую из возможных последовательностей элементов (букв, цифр, знаков, символов). В диагностике изучается связь между системой состояний и системой признаков.

Рассмотрим системы, в которых одно из состояний обязательно реализуется, а два или более состояний одновременно невозможны. Система А, имеет n возможных состояний с вероятностями Р(А1), Р(А2),…, Р(Аn), при этом очевидно, что

i=1

Энтропия (степень неопределенности) системы А в теории информации определяется выражением:

Cтепень неопределенности, энтропия системы А, зависит от числа возможных состояний n (бросание монеты или кубика) и от соотношения вероят

23

ностей Р(Аi) того или другого состояния.

Энтропию нагляднее представить с помощью двоичных логарифмов, при этом в качестве единицы энтропии принимается степень неопределенности системы, имеющей два равновероятных состояния (бросание монеты) Р(А1) = Р(А2) = 0,5. Тогда по формуле (4.2) находим

H (A)= −P(A1 )log2 P(A1 )− P(A2 )log2 P(A2 )=

Бит – единица энтропии, которая соответствует степени неопределенности системы, имеющей два возможных равновероятных состояния. Название бит происходит от английских слов binary digit (двоичная единица)

Основные свойства энтропии.

1.Если система А имеет одно из возможных состояний Аk с вероятностью Р(Аk) = 1, то энтропия такой системы Н(А) = 0.

2.Энтропия системы, имеющей n равновероятных состояний P(Ai )= 1n , равна логарифму числа состояний:

3. Если система А имеет n возможных состояний, то энтропия будет максимальной, когда все состояния равновероятны. Из этого свойства следует, что для произвольной системы всегда соблюдается условие

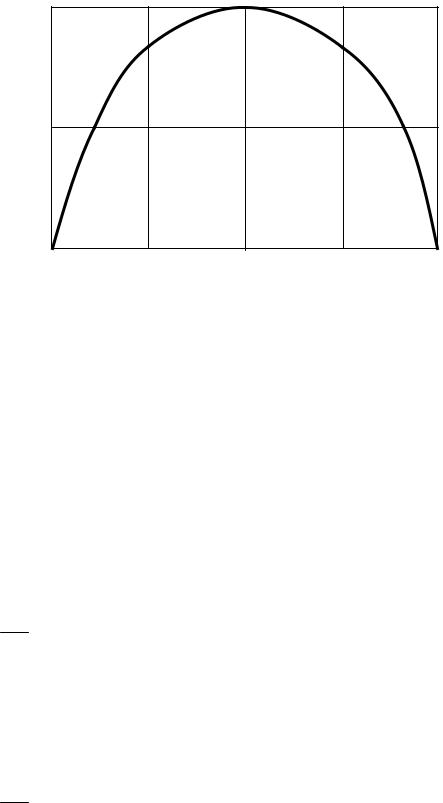
В задачах технической диагностики часто встречаются системы с двумя возможными состояниями, которые называют бинарной системой. Если для бинарной системы вероятность первого состояния равна Р, то второго – 1 – Р. Для наглядности на рис. 4.2 представлена зависимость энтропии бинарной системы от вероятности одного из состояний Р1. При этом Р2=1- Р1, а энтропия

В общем случае, если система состоит из n элементов, каждый из которых может иметь m состояний, число возможных состояний системы равно

H

0,5

Рис. 4.2. Зависимость энтропии бинарной системы от вероятности первого состояния

Количество диагностической информации оценивается величиной

где H* (A)– энтропия системы после внесения диагностической информации.

В нашем примере до получения первого сообщения мы имеем вероятности двух состояний подшипника: исправного P(D1) = 0,998 и дефектного P(D2) = 0,002. Энтропия системы диагнозов

H0 (D)= −P(D1 )log2 P(D1 )− P(D2 )log2 P(D2 )= = − lg12 (0,998lg 0,998 + 0,002 lg 0,02)= 0,02,

т. е. мы имеем большую вероятность исправного состояния подшипника.

После получения первого сообщения имеем вероятности двух состояний подшипника: исправного P(D1) = 0,28 и дефектного P(D2) = 0,72. Энтропия

H1 (D)= −P(D1 )log2 P(D1 )− P(D2 )log2 P(D2 )= = − lg12 (0,28lg 0,28 + 0,72 lg 0,72)= 0,857.

25

В результате мы имеем большую степень неопределенности состояния подшипника, а количество полученной диагностической информации от первого сообщения:

J1 = H0 (D)− H1(D)= 0,002 −0,857 = −0,855.

Знак минус означает, что полученная информация вносит большую неопределенность о состоянии подшипника, но, несомненно, является полезной, так как свидетельствует о возможном дефекте.

После получения второго сообщения имеем P(D1) = 0,01 и P(D2) = 0,99, аналогично

H2 (D)=0,0623.

Количество полученной диагностической информации от второго сообщения

J2 = H1(D)− H2 (D)= 0,857 −0,0623 = 0,7947.

Таким образом, мы убедились, что количество информации определяется не только техническими свойствами самого СТД как средства измерения параметра, а в большей степени тем, как это техническое средство используется, какова технология, алгоритм диагностирования. Оптимальные решения задач технической диагностики могут быть получены только в результате анализа множества состояний, в которых объект диагностирования может находиться в период эксплуатации. В связи с этим требуются специальные методы для теоретического анализа множества возможных состояний технических объектов. Подобные методы основываются на исследовании аналитических описаний или графо - аналитических представлений основных свойств объекта диагностирования, которые могут быть названы их диагностической моделью.

Представим в аналитическом виде диагностическую модель греющейся буксы. Перегрев корпуса буксы Θ является функцией многих аргументов

Θ = f (T ,V , P, B, R, L, F ) ,

где Т – продолжительность работы; V – скоростной режим поезда; Р – загрузка вагона; В – состояние пути (балльность);

R – профиль пути в плане (кривые малого радиуса); L – солнечное излучение;

F – силы сопротивления качению в подшипнике.

Элементарный анализ свидетельствует о том, что первые шесть аргументов не зависят от технического состояния подшипника, которое определяется, в основном, силами сопротивления качению F. Представим зависимость перегрева произведением двух функций:

Θ = f1 (T ,V , P, B, R, L,) f2 (F ) .

26

В результате для специалиста становится очевидным решение проблемы получения необходимого количества информации путем определения безразмерного параметра К0 – отношения перегрева каждой буксы к среднему значению перегрева по вагону или по его стороне Θср, тогда с учетом того, что

f1(T ,V , P, B, R, L,) для всех букс стороны вагона одинакова, имеем

чению перегрева по стороне вагона, К0 зависит только от технического состояния подшипника.

4.2. Информация о состоянии сложной системы

Важное значение имеет системный подход к решению задачи распознавания состояния объекта, состоящего из нескольких систем и (или) взаимодействующего с другими объектами.

Объект диагностирования, как правило, представляет собой ряд систем, которые функционально взаимосвязаны, либо является системой, функционально связанной с другими системами. Вагон также представляет собой ряд систем, называемых сборочными единицами (кузов, рама, тележки, автосцепка, автотормоз), которые функционально связаны между собой, а также с другими системами: путь, локомотив, горочные замедлители, погрузочно-разгрузочные устройства и др.

Вполне вероятно, что информацию относительно системы А, недоступной для распознавания, можно получить с помощью наблюдения за другой, связанной с ней системой В, более доступной для распознавания. Подобный пример уже упоминался, когда рассматривалась проблема обнаружения дефектов на поверхности катания колес через виброускорение рельса. При этом важное значение имеет степень взаимосвязи между состоянием рассматриваемых систем.

В общем случае энтропия системы АВ может быть определена аналогично формуле (4.2):

Если системы А и В независимы, т. е. реализация одного из состояний системы Аi не влияет на вероятность возможного состояния системы Вj и наоборот, то в этом случае

27

Энтропия двух статистически независимых систем в соответствии с (4.10) и (4.11) и с учетом того, что

Следовательно, при объединении двух независимых систем энтропия возраста-

ет. Для зависимых систем вероятность возможного состояния одной из них (системы В) будет зависеть от того, в каком состоянии другая, связанная с ней система (система А):

Учитываем, что

j=1

Равенство (4.15) является следствием того, что вне зависимости от реализации того или иного состояния Ai одно, и только одно, из состояний Вj обязательно реализуется. Решая совместно (4.10) и (4.14), получаем энтропию сложной системы, объединяющей две зависимые системы А и В:

где H (A / B) - условная энтропия системы А относительно системы В, представляет собой энтропию системы А при различных возможных реализациях системы В, и наоборот.

Понятие условной энтропии определяется из равенства:

n

H (B / A) = ∑P(Ai )H (B / Ai ) =

i=1

n m

−∑∑P(Ai )H (Bj / Ai )log2 P(Bj / Ai ), (4.17)

i=1 j=1

28

где H (B / Ai ) - частная условная энтропия, которая характеризует связь систем А и В. Если такая связь отсутствует, то P(B j / Ai ) = P(B j ) и из соотношений

(4.12) и (4.17) получим

Переходя к оценке информации, можно определить информативность системы В относительно системы А следующим равенством:

Это разность первоначальной энтропии системы А и ее энтропии после того,

как стало известно состояние систем. Определив H (A / B) из (4.16), получим соотношение

Обозначив индексом i реализацию того или иного состояния системы А, а индексом j – системы В, после преобразований определяем информацию, которую дает состояние Вj относительно состояния Аi :

Величина J Ai (B j ) называется элементарной информацией состояния Вj о

состоянии Аi. Иными словами, если априорная вероятность состояния Аi равна Р(Аi), а после получения сигнала о состоянии Вj она изменилась и стала Р(Ai/Bj), то знание состояния Вj дает некоторую информацию относительно Аi, определяемую (4.21). Если же сигнал Вj встречается одинаково часто, как при наличии состояния Аi, так и при любых других состояниях системы А, то , очевидно, что

он не несет информации о состоянии Аi, и из (4.21) следует J Ai (Bj )= 0 . Ин-

формация J Ai (Bj )может принимать отрицательное значение в том случае, если при получении сигнала Вj вероятность состояния Аi уменьшается.

Вкачестве примера рассмотрим две взаимосвязанные системы: А – буксовый подшипник;

В– колесная пара и состояния этих систем:

А2 – перегрев, разрушение подшипника;

29