9. Задачи объезда
К этому классу относят ряд задач, связанных с обслуживанием группы объектов, причем целью является составление графика проезда по всем участкам сети или посещения всех объектов, характеризуемого минимальными суммарными затратами. К этой группе относят знаменитую задачу о маршруте китайского почтальона (алгоритм поиска кратчайших эйлеровых циклов) и задачу о маршруте коммивояжера (алгоритм поиска кратчайших гамильтоновых циклов, на основе метода ветвей и границ Литтла).
Решение задач, которые связаны с нахождением оптимального способа объезда определенных объектов, связанных между собой дорогами, или, расположенных вдоль дорог, как правило, относят едва ли не к основным функциям отдела логистики предприятий.
9.1. Маршрут китайского почтальона
Задачи объезда объектов, расположенных вдоль дорог, могут возникать в разнообразных областях, например при доставке молока или почты, сборе домашнего мусора, проверке электрических, телефонных или железнодорожных линий (и вообще, инспектировании любых распределенных систем), разбрасывании соли и песка во время гололеда, уборке коридоров в больших зданиях.
Обычно такого рода задачи называют задачами китайского почтальона.
НЕОБХОДИМАЯ ТЕОРЕТИЧЕСКАЯ ИНФОРМАЦИЯ
Цикл, проходящий через все ребра графа ровно по одному разу, называется эйлеровым циклом. Эйлеров цикл не обязательно существует в графе. Известен очень простой критерий, по которому можно определить наличие в произвольном графе эйлерова цикла.
Утверждение 1. Для существования в связном неориентированном графе эйлерова цикла необходимо и достаточно, чтобы степени всех вершин графа были четные.
Утверждение 2. Для существования в связном ориентированном графе эйлерова цикла необходимо и достаточно, чтобы для каждой вершины графа полустепень захода была равна полустепени исхода.
Определить, существует ли эйлеров цикл, несложно. Вопрос в том, как его найти. Флёри дал очень простой алгоритм построения эйлерова цикла в неориентированном графе: начиная с некоторой вершины идти по графу, вычеркивая пройденные ребра. Не проходить по ребру, если его удаление приведет к разбиению графа на две связные компоненты (изолированные вершины не считаются). Этот алгоритм строит цикл, если он существует, но не может помочь в решении задачи, если такого цикла нет, а нужен способ оптимального обхода ребер графа, пусть и с некоторыми повторениями.
ПОСТАНОВКА ЗАДАЧИ
Ребрам графа приписаны положительные веса. Найти цикл, проходящий через каждое ребро графа по крайней мере, один раз и такой, что для него общий вес минимален.
НЕОБХОДИМЫЕ УТОЧНЕНИЯ
Очевидно, что если граф G содержит эйлеров цикл, то любой такой цикл будет оптимальным, так как каждое ребро проходится только один раз, и вес этого цикла будет равен
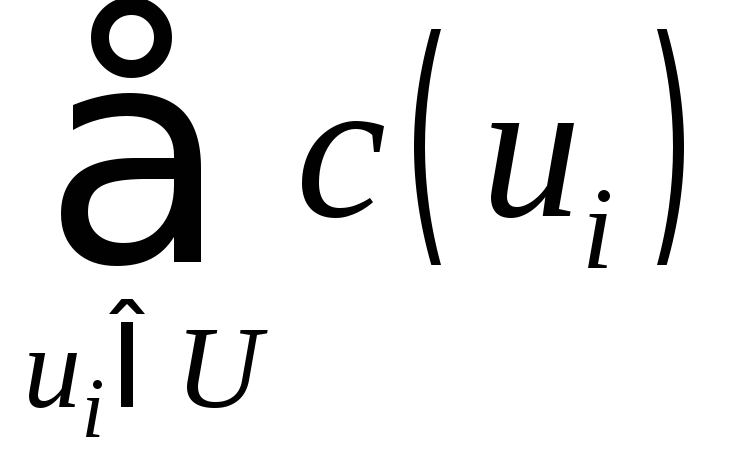.Если граф такого цикла не содержит, то в нем есть вершины нечетной степени. Однако поскольку вообще в графе сумма степеней всех вершин всегда четна (и равна удвоенному количеству ребер), то сумма степеней по всем вершинам, имеющим нечетную степень, тоже четна. Откуда напрямую следует, что количество вершин нечетной степени - четно.
ОПИСАНИЕ АЛГОРИТМА
Основная идея
Глобальная цель - искусственным образом привести граф к виду, когда эйлеров цикл существует, т.е. сделать все вершины нечетной степени вершинами со степенью четной: это возможно путем добавления парных ребер к уже существующим ребрам графа. Тогда нахождение в новом графе эйлерова цикла даст и решение задачи.
ПРИМЕР ЗАДАЧИ
Допустим, определенный район города обслуживается единственной мусороуборочной машиной. Схема района приведена на рис. 9.1. Найти оптимальный (характеризуемый минимальным километражом) способ объезда района для сбора мусора (предполагается, что мусорные контейнеры расположены вдоль всех дорог).
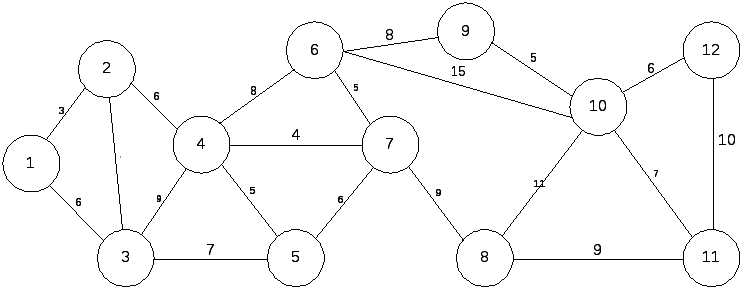
Рис. 9.1. Схема района
При решении задачи приходится удвоить некоторые ребра графа для того, чтобы обеспечит четность всех его вершин (рис. 9.2).
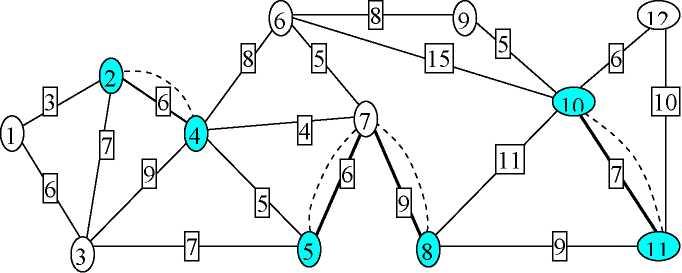
Рис. 9.2. Дополненный
граф
Используя алгоритм Флери, находим найти эйлеров цикл графа G*, записывая проходимые вершины в массив P[i] и соответствующий ему оптимальный цикл первоначального графа G. P[i]={1,2,4,6,9,10,12,11,10,6,7,8,10,11,8,7,5,3,4,5,7,4,2,3,1}. Вес полученного цикла равен 281.