2.2 Реверсивний 4-х розрядний лічильник ( ап2)

Лічильник імпульсів - це автомат з пам'яттю, призначений для підрахунку кількості імпульсів і перетворення їх в паралельний двійковий код.

Робота лічильника полягає в наступному: за допомогою вхідного сигналу в лічильник записуються числа, рівні кількості що поступили на вхід активних сигналів. Кожному числу відповідає певний внутрішній стан лічильника. Робота лічильника полягає в послідовному переході з одного стану в інший під впливом вхідного сигналу.

Лічильник має певну, кінцеву кількість внутрішніх станів. Після приходу останнього активного сигналу лічильник переходить в початковий стан і починається новий цикл його роботи.

По виду рахунку лічильники бувають:

• лічильник прямого рахунку ( підсумовує);

• лічильник зворотного рахунку (показує різницю);

• реверсивний лічильник (підсумовує або віднімає);

• лічильник по модулю ( модуль визначає кількість робочих станів);

• лічильники двійково-десятичний;

• лічильник, працюючий в коді Грея.

В своїй курсовій роботі я синтезую реверсивний 4-х розрядний лічильник за допомогою RS-тригера та мікросхеми 1533 ЛА3.

На рис.2.21 зображений граф переходів реверсивного

4-х розрядного лічильника.

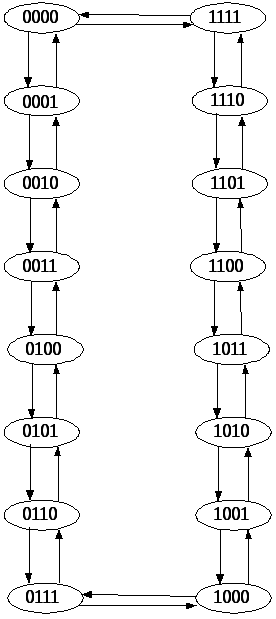
Рис.2.21

0	0	0	0	0	0	0	0	1	0	~	0	~	0	~	1	0
0	0	0	0	1	0	0	1	0	0	~	0	~	1	0	0	1
0	0	0	1	0	0	0	1	1	0	~	0	~	~	0	1	0
0	0	0	1	1	0	1	0	0	0	~	1	0	1	0	0	1
0	0	1	0	0	0	1	0	1	0	~	~	0	0	~	1	0
0	0	1	0	1	0	1	1	0	0	~	~	0	1	0	0	1
0	0	1	1	0	0	1	1	1	0	~	~	0	~	0	1	0
0	0	1	1	1	1	0	0	0	1	0	0	1	0	1	0	1
0	1	0	0	0	1	0	0	1	~	0	0	~	0	~	1	0
0	1	0	0	1	1	0	1	0	~	0	0	~	1	0	0	1
0	1	0	1	0	1	0	1	1	~	0	0	~	~	0	1	0
0	1	0	1	1	1	1	0	0	~	0	1	0	0	1	0	1
0	1	1	0	0	1	1	0	1	~	0	~	0	0	~	1	0
0	1	1	0	1	1	1	1	0	~	0	~	0	1	0	0	1
0	1	1	1	0	1	1	1	1	~	0	~	0	~	0	1	0
0	1	1	1	1	0	0	0	0	0	1	0	1	0	1	0	1
1	0	0	0	0	1	1	1	1	1	0	1	0	1	0	1	0
1	1	1	1	1	1	1	1	0	~	0	~	0	~	0	0	1
1	1	1	1	0	1	1	0	1	~	0	~	0	0	1	1	0
1	1	1	0	1	1	1	0	0	~	0	~	0	0	~	0	1
1	1	1	0	0	1	0	1	1	~	0	0	1	1	0	1	0
1	1	0	1	1	1	0	1	0	~	0	0	~	~	0	0	1
1	1	0	1	0	1	0	0	1	~	0	0	~	0	1	1	0
1	1	0	0	1	1	0	0	0	~	0	0	~	0	~	0	1
1	1	0	0	0	0	1	1	1	0	1	1	0	1	0	1	0
1	0	1	1	1	0	1	1	0	0	~	~	0	~	0	0	1
1	0	1	1	0	0	1	0	1	0	~	~	0	0	1	1	0
1	0	1	0	1	0	1	0	0	0	~	~	0	0	~	0	1
1	0	1	0	0	0	0	1	1	0	~	0	1	1	0	1	0
1	0	0	1	1	0	0	1	0	0	~	0	~	~	0	0	1
1	0	0	1	0	0	0	0	1	0	~	0	~	0	1	1	0
1	0	0	0	1	0	0	0	0	0	~	0	~	0	~	0	1

t

t+1

x

y1

y2

y3

y4

y1

y2

y3

y4

За допомогою графа переходів будуємо функціональну таблицю 2.21

YS1

YR1

YS2

YR2

YS3

YR3

YS4

YR4

Після таблиці функціональності будуємо карти Карно, щоб отримати рівняння для функцій , описуючих вхідні сигнали тригера.

Y_S1 = x y₁ y₂y₃y₄ + x y₁ y₂ y₃ y₄

Y_R1 = xy₁y₂y₃y₄ + x y₁y₂ y₃ y₄

Y_S2 = x y₂ y₃ y₄ + x y₂ y₃ y₄

Y_R2 = x y₂ y₃ y₄ + x y₂ y₃ y₄

Y_S3 = x y₁y₂y₄ + x y₃y₄ + xy₃y₄

Y_R3 = x y₂y₃y₄ + xy₁y₃y₄ + xy₃y₄

Y_S4 = y₄

Y_R4 = y₄

Рис.2.22

Приводимо отримані функції до базису Шефера для мікросхеми 1533 ЛА3:

Y_S1 = x y₁ y₂y₃y₄ + x y₁ y₂ y₃ y₄ = x y₁ y₂y₃y₄ x y₁ y₂ y₃ y₄ =

=x y₁ y₂ y₃ y₄ x y₁ y₂ y₃ y₄

Y_R1 = xy₁y₂y₃y₄ + x y₁y₂ y₃ y₄ = xy₁y₂y₃y₄ x y₁y₂ y₃ y₄ = x y₁ y₂ y₃ y₄ x y₁ y₂ y₃ y₄

Y_S2 = x y₂ y₃ y₄ + x y₂ y₃ y₄ = x y₂ y₃ y₄ x y₂ y₃ y₄ = x y₂ y₃ y₄ x y₂ y₃ y₄

Y_R2 = x y₂ y₃ y₄ + x y₂ y₃ y₄ = x y₂ y₃ y₄ x y₂ y₃ y₄ = x y₂ y₃ y₄ x y₂ y₃ y₄

Y_S3 = x y₁y₂y₄ + x y₃y₄ + xy₃y₄ = x y₁ y₂ y₄ x y₃ y₄ x y₃ y₄ =

=x y₁ y₂ y₄ x y₃ y₄ x y₃ y₄

Y_R3 = x y₂y₃y₄ + xy₁y₃y₄ + xy₃y₄ = x y₂y₃y₄ x y₁y₃y₄ xy₃y₄ =

=x y₂ y₃ y₄ x y₁ y₃ y₄ x y₃ y₄

Y_S4 = y₄

Y_R4 = y₄

За допомогою отриманих рівнянь будуємо схему реверсивного

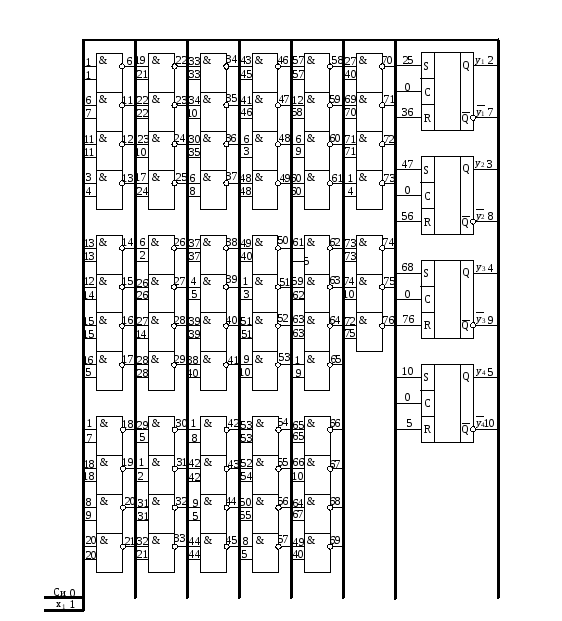4-х розрядного лічильника:

Рис.2.23