Механика_20

ЛАБОРАТОРНАЯ РАБОТА №20

ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СИЛЫ ТЯЖЕСТИ С ПОМОЩЬЮ

МАТЕМАТИЧЕСКОГО И ФИЗИЧЕСКОГО МАЯТНИКОВ

Принадлежность: универсальный маятник с миллисекундомером (ФПМ -04).

Цель работы: 1. изучить физический и математический маятники и связанные с ними основные физические законы и понятия;

2. научиться с их помощью экспериментально определять ускорение силы тяжести.

Теория

Гармонические колебания представляют собой периодический процесс, в котором смещение системы от положения равновесия происходит с течением времени по закону синуса или косинуса, т.е. по гармоническому закону:

X Asin( t 1) или X Acos( t 2)

Величина А (наибольшее значение отклонения) называется амплитудой колебания, - круговой частотой колебаний. Через промежуток времени

T 2 / функции синуса и косинуса проходят через одни и те же значения, т.е. движение повторяется. Этот промежуток времени называется периодом колебаний. Аргумент тригонометрической функции t 1 или

t 2 называется фазой колебаний.

Рассмотрим механическую колебательную систему, состоящую из практически нерастяжимой, очень легкой нити и подвешенного к ней груза массы m, размеры которого малы по сравнению с длиной нити, а масса велика по сравнению с ее массой (рис.1). Такая система ближе всего подходит по своим свойствам к идеальному математическому маятнику.

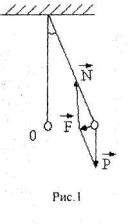
Математическим маятником называют систему, представляющую собой материальную точку, подвешенную на тонкой невесомой и

нерастяжимой нити.

Отклоним грузик от положения равновесия в сторону, а затем отпустим. Грузик будет двигаться к положению равновесия с ускорением х",

которое возникло под действием силы, натяжении нити N и силы тяжести

P mg .

Достигнув положения равновесия 0, где ускоряющая сила равна нулю,

грузик пройдет по инерции положение равновесия и далее будет тормозится той же силой, которая его ускоряла ранее. Затем он остановится и пойдет обратно. Так возникнут собственные колебания маятника. В общем случае колебания маятника не являются гармоническими, но они близки к

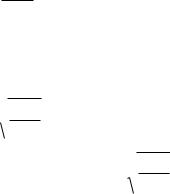
где m - масса тела.

Момент силы, направлен так, что тело движется к положению равновесия, в котором момент М становиться равным нулю.

В соответствии с основным законом динамики вращательного движения: M J напишем уравнение моментов, полагая, что трение на оси отсутствует:

J J mgd sin

где J – момент инерции тела относительно горизонтальной оси, проходящей через точку 0, - угловое ускорение (вторая производная угла смещения по времени).

При малых углах отклонения sin , тогда

J mgd 0

или

mgd 0 (9)

J

Это уравнение по виду совпадает с уравнением (5). Следовательно,

будет изменятся по гармоничному закону с частотой

mgd J

и с периодом T 2 J mgd

Период колебаний физического маятника существенно зависит не только от расстояния от оси до центра тяжести d, но и от момента инерции маятника J относительно оси 0, т.е от расположения отдельных элементов массы маятника.

Из сопоставления формул (8) и (10) получается, что математический маятник с длиной lïð J /md будет иметь такой же период колебаний, как и данный физический маятник. Величину lïð называют приведенной длиной физического маятника. Таким образом, приведенная длина физического маятника – это длина математического маятника, период колебания которого

совпадает с периодом колебаний данного физического маятника.

Если к оси физического маятника подвесить «математический» маятника, т.е. грузик m малых размеров на нити и подобрать длину этой нити так, чтобы она была равной приведенной длине физического маятника, то отклоненные на одинаковый угол, оба маятника колеблются одинаковым периодом, так что грузик все время находится в одной и той же точке физического маятника. Центр качаний всегда лежит дальше от оси вращения,

чем центр тяжести (lïð d) .

Так как период маятника зависит от g. то маятником можно пользоваться для определенной величины g. При точных измерениях ни один маятник нельзя рассматривать как математический. Поэтому при точных измерениях для расчета силы тяжести пришлось бы пользоваться формулой

(10). Но расчет момента инерции маятника не может быть произведен с большой точностью.

Для устранения этих трудностей используют свойство центра качаний,

которое заключается в следующем. Если перенести точку подвеса физического маятника 0 (рис.3) в центр качаний 0, то прежняя точка подвеса окажется новым центром качаний. Точка подвеса и центр качаний обратимы.

Таким образом, во всяком физическом маятнике всегда можно найти две точки, что при последовательном подвешивании маятника за ту или другую из них период остается одним и тем же. Расстояние между этими точками определяет собой приведенную длину данного маятника. На этом свойстве (свойства сопряженности) основано применение оборотного маятника для определения ускорения силы тяжести g.

Рис.4

Оборотные маятники в зависимости от предъявляемых к ним требований имеют самую различную форму. Обычно они состоят из металлического стержня длиной свыше 1 метра, на поверхность которого нанесены миллиметровые деления. По стержню могут передвигаться и закрепляться тяжелые чечевицы (грузы I и II) и опорные призмы А и В.

Различные комбинации чечевиц и их положений на стержне с опорными призмами дают различные типы оборотных маятников.

Один из них изображен на рис.4, где С — центр тяжести маятника, d1 -

расстояние от ребра призмы А до С. d2 -расстояние от ребра призмы В до С,

ТA – период качания маятника вокруг ребра призмы А, ТB – период качания маятника вокруг ребра призмы В. Если амплитуда колебаний маятника мала,

то период колебания с достаточной точностью определяется формулой:

T 2 J (10) mgd

Тогда ТA и ТB соответственно равны:

TÂ 2 JÂ mgd2

где JA и JB – момент инерции маятника относительно ребра (осей вращения)

призмы А и В.

Пользуясь теоремой Гюйгенса-Штейнера, можно доказать, что в случае

равенства периодов TA=TB=TR, величину ускорения можно определить по

где lR d1 d2 – приведенная длина.

Однако добиться полного совпадения периода колебания около обеих осей чрезвычайно трудно. Обычно в процессе измерения находят такое положение призм и чечевиц, при котором маятник, подвешенный на призмах

А и В, колеблется приблизительно с одинаковыми периодами (TA TB с

точностью до 0,5%) и рассчитывая g по формуле (12), определяют погрешность.

Точное значение g вычисляют по формуле Бесселя, вывод которой

приведен ниже.

Если расстояние между ребрами призм равно lR d1 d2 , истинный

период маятника, имеющего такую приведенную длину, равно TR, то в действительности мы при наблюдении колебаний около обеих осей получим

Возведя в квадрат и деля первое равенство на каждое из последующих,

найдем:

IRTA2 IATR2 и IRTÂ2 IÂTR2 (14)

Используя формулу (11) и теорему Гюйгенса-Штейнера, напишем для приведенных длин lA и lB следующие соотношения:

Подставив значения lA и, lB в равенство (14), получим:

Исключая отсюда JC /m, получим d1TA2 dTB2 (d1 d2 )TR2

Откуда

TR2 d1TA2 d2TB2 d1 d2

Это равенство можно записать в виде:

Из первого равенства (13) найдем g 4 2lR /TR2 и подставим в него значение

TR2 из (15)

После очевидных преобразований получим:

Эта формула носит название формулы Бесселя. Она позволяет достаточно просто и с необходимой степенью точности найти величину,

ускорения при приближенном равенстве периодов колебаний оборотного маятника.

Если TA и TB близки к друг другу, а величина d1 и d2 сильно отличаются одна от другой (для чего обычно делают одну чечевицу полой, а другую сплошной), то d1 и d2 достаточно измерить с точностью до миллиметра. Для этого маятник осторожно снимают с подвеса и кладут на подставку с острием. Добиваются уравновешивания маятника. Расстояние от острия до

опорных призм маятника при равновесии дают величины d1 и d2.

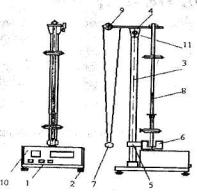
Описание прибора В работе используется универсальный маятник, общий вид которого

представлен на рис.5.

Рис. 5

Основание 1 оснащено регулируемыми ножками 2, которые позволяют произвести выравнивание прибора. В основании закреплена колонка 3, на которой зафиксирован верхний кронштейн 4 и нижний кронштейн 5 с

фотоэлектрическим датчиком 6. После отвинчивания воротка 11 верхний можно поворачивать вокруг колонки. Затяжение воротка 11 фиксирует кронштейн в любом произвольно выбранном положении, с другой стороны кронштейн 4 находится математический маятник 7, с другой - на вмонтированных вкладышах оборотный маятник 8. Длину математического маятника можно регулировать при помощи воротка 9, а величину можно определить при помощи шкалы на колонке 3.

Оборотный маятник выполнен в виде стального стержня, на котором фиксированы две повернутые друг к другу ребрами призмы и две чечевицы.

На стержне через 10 мм выполнены кольцевые нарезки, служащие для точного определения длины оборотного маятника (расстояние между ребрами призмы). Призмы и чечевицы можно перемещать вдоль оси стержня и фиксировать в любом положении. Нижний кронштейн вместе с фотоэлектрическим датчиком можно перемещать вдоль колонки и фиксировать в произвольно выбранном положении.