Тема 5.3. Смешанное произведение векторов

Литература: [1], гл. 9, §3, стр.221–225; [2], гл.1, §3-5, стр.29–33; [27], гл.6, § 55, стр. 196-200.

Основные определения, теоремы и формулы

Смешанным произведениемтрех векторовив ориентированном векторном пространстве называется скалярное произведение векторови.

Геометрически смешанное произведениевекторов интерпретируется как объем параллелепипеда, построенного на векторах как на сторонах, взятый со знаком плюс, если тройка векторов правая, и со знаком минус, если тройка векторов левая.

Смешанное произведение векторов иобозначаетсяили.

Теорема 1.Смешанное произведение векторовиравно нулю тогда и только тогда, когда эти векторы компланарны.

Теорема 2.Если векторыиимеют координаты,относительно произвольно базиса, то

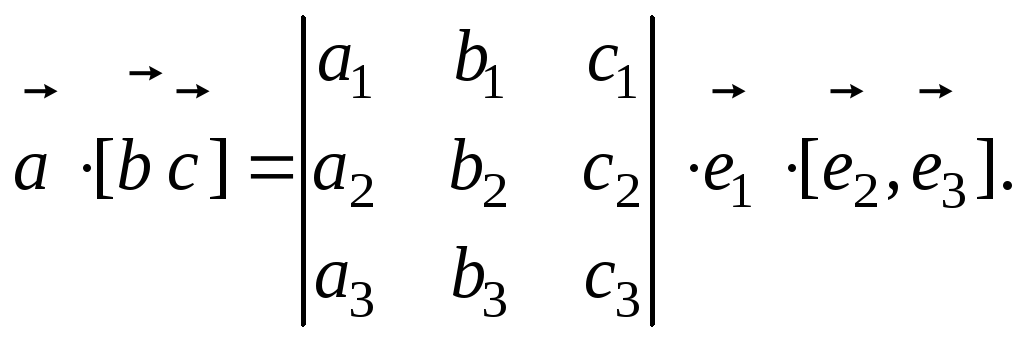
Вопросы для самоконтроля

1. Что называется смешанным произведением:

а) некомпланарных векторов , б) компланарных векторов?

2. Сформулировать основные свойства смешанного произведения векторов.

3. Что можно сказать о векторах если

а) =0, б)_,в)

4. Что можно сказать о векторах , если известно, что:

а) б), в), где– некоторое вещественное число, г)?

5. Сравните и. В каком случае эти величины равны?

6. Пользуясь приведенной выше формулой для вычисления смешанного произведения векторов через их координаты в произвольном базисе получите формулу для случаев, если базис: а) ортонормированный правый, б) ортонормированный левый.

7. Найти вектор удовлетворяющий условиюгдеи– данные векторы, а– данное число. Всегда ли уравнение имеет решение? Выясните геометрический смысл решения уравнения.

8. Верно ли, что для любых векторов :

а) () + () + () + () + () = 0,

б) ?

Если нет, то, для каких векторов выполняется каждое из равенств а), б)?

Пример 1.Вычислить произведение

Решение.Согласно свойствам векторные многочлены в смешанном произведении векторов перемножаются по тем же правилам, что и алгебраические многочлены. Тогда

Произведения равны нулю, а произведениеследовательно,

Пример 2.Вычислить объем тетраэдра, вершины которого находятся в точках

Решение.Так как объемтетраэдра, построенного на векторахравен 1/6 объема параллелепипеда, построенного на тех же векторах, тоНайдем координаты векторовТогда

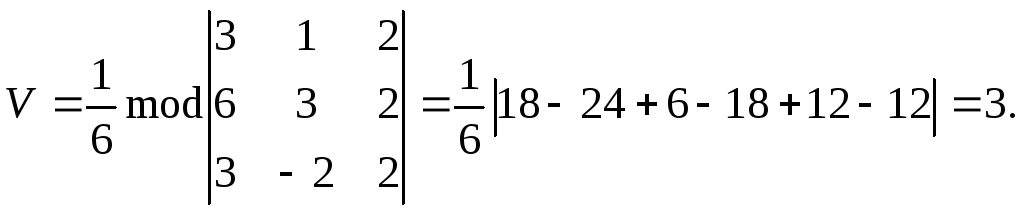
Задачи

1. Вычислить смешанные произведения:

а) б)если

2. Вектор перпендикулярен векторамивеличина угла между которыми равна 30⁰. Зная, чтовычислить

3. Найти смешанное произведение векторов (2,–3,1),(1,1,2),(3,1,–1), заданных своими координатами в ортонормированном

а) правом базисе, б) левом базисе.

4. Доказать что для любых трёх векторов и вещественных чиселвекторыкомпланарны.

5. Найти длину высоты параллелепипеда ABCDA₁B₁C₁D₁, построенного на векторах(4,3,0),,(–3,–2,3).

6. Объём тетраэдра равен 5, три его вершины находятся в точках в точках А(2,1,–1),В(3,0,1), С (2,–1,3). Найти координаты четвертой вершиныесли известно, что она лежит на оси ординат.

7. Доказать, что отношение объёма параллелепипеда к объёму тетраэдра, вершинами которого являются одна из вершин параллелепипеда и центры трёх граней, не содержащих этой вершины, не зависит от выбора параллелепипеда и его вершины.

8. Дан тетраэдр ABCD и точкаSна ребреAB. Доказать, что середины отрезковAD, BC, SDиSCлежат в одной плоскости.

Домашнее задание

1. Найти смешанные произведения иесли известно, что

2. Найти смешанное произведение векторов заданных своими координатами в ортонормированном левом базисе, и определить ориентацию базисав каждом из следующих случаев:

а) (2,–3,1),(1,1,2),(3,1,–1),

б) (–2,1,5),(3,0,2),(–1,4,2),

в) (1,–1,1),(5,2,–3),(1,4,–2).

3. Найти отношение объема параллелепипеда к объему тетраэдра, ребрами которого служат диагонали трех граней параллелепипеда, выходящие из одной его вершины.

4. Точки и делят ребраSA, SBиSCтетраэдраSABCв отношениях= (SA, A’),= (SB,B’),= (SC,C’), где все числаположительны. Найти отношение объемов тетраэдровиSABC.

Задачи повышенной трудности

1. Доказать, что объемы двух тетраэдров с равными трехгранными углами при одной вершине относятся как произведения ребер, сходящихся в вершинах этих углов.

2. Основанием пирамиды служит параллелограмм. В каком отношении делится объем пирамиды плоскостью, проходящей через сторону основания и среднюю линию противолежащей грани?